4.3 解直角三角形及其应用（2）

课件14张PPT。4.3 解直角三角形及其应用（2）湖南省新邵县酿溪中学王军旗 如图，一颗大树在一次强烈的台风中与地面10米处折断倒下，树顶落在离树根24米处，问大树在折断之前高多少米？ 思考（1）这个问题转化为几何问题就是:已知:

求:_____新课引言Rt△ABC中，
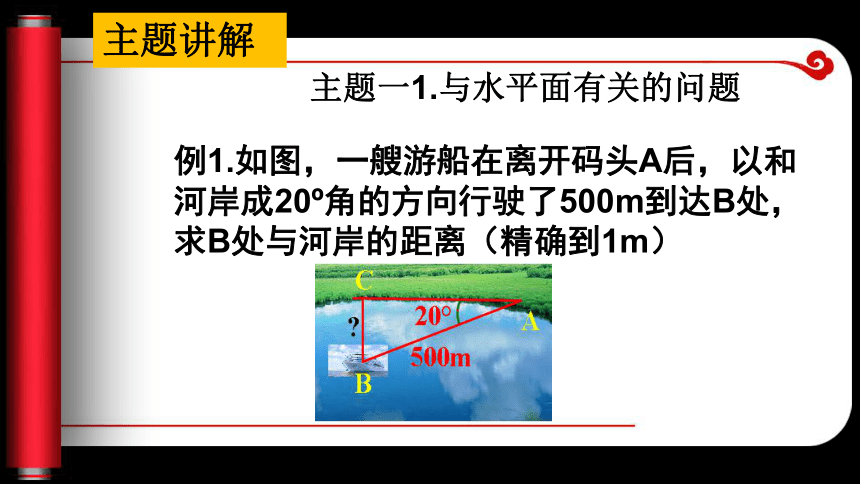
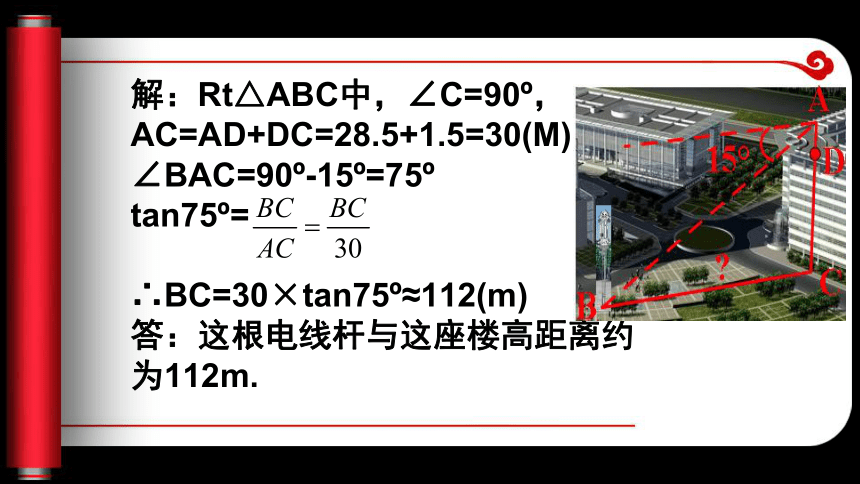
∠C=90o,AC=10m,BC=24m.AC+AB 这个问题转化为数学问题就是已知直角三角形的两条直角边，求斜边和一直角边的和的问题，关键是求出斜边。可以利用勾股定理求出AB。所以解直角三角形应用问题，关键是把实际问题 转化为直角三角形问题。例1.如图，一艘游船在离开码头A后，以和河岸成20o角的方向行驶了500m到达B处，求B处与河岸的距离（精确到1m）主题讲解主题一1.与水平面有关的问题解：在Rt△ABC中，AB=500, ∠A=20o SinA= , BC=AB×sinA =500×sin20o≈171(m)答：B处与河岸的距离约为171m例2.如图，在高为28.5m的楼顶平台D处，用仪器测得一路灯电线杆底部B的俯角为14o2′，仪器高度AD为1.5m，求这根电线杆与这座楼的距离（精确到1m）。主题二、垂直方向的问题解：Rt△ABC中，∠C=90o，AC=AD+DC=28.5+1.5=30(M)∠BAC=90o-15o=75otan75o= ∴BC=30×tan75o≈112(m)答：这根电线杆与这座楼高距离约为112m.(2009中山)如图所示，A、B两城市相距100km. 现计划在这两座城市间修筑一条高速公路（即线段AB），经测量森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上. 已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内. 请问：计划修筑的这条高速公路会不会穿越保护区. 为什么？答：森林保护区的中心与直线变式练习则∠APC=30 o，∠BPC=45 o，AC=PC·tan30 o,BC=pctan45 oAC+BC=AB, ∴PC·tan30 o+pctan45 o=100 ∴PC ≈63.4>50 C解：过点P作PC⊥AB，C是垂足，答：这条高速公路不会穿越保护区 2、（2010年兰州）如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB长为4米.
．（1）求新传送带AC的长度；
（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由分析：过A点做AD ⊥CB于D，构造直角三角形。问题的关键是求AC,BC,可以先解直角三角形ABD,求出AD,BD,再解直角三角形ABC求出AC,CD，从而就可以求出BC. 小结 解与直角三角形应用问题时，关键是把实际问题转化为几何问题，要善于分析题意，找到已知哪个直角三角形中的什么量。要求什么量。利用什么关系求。1(2009成都)某中学九年级学生在学习“直角三角形的边角关系”一章时，开展测量物体高度的实践活动，他们要测量学校一幢教学楼的高度．如图，他们先在点C测得教学楼AB的顶点A的仰角为30°，然后向教学楼前进60米到达点D，又测得点A的仰角为45°。请你根据这些数据，求出这幢教学楼的高度．(计算过程和结果均不取近似值)作业2.（2009仙桃）如图所示，小华同学在距离某建筑物6米的点A处测得广告牌B点、C点的仰角分别为52°和35°，则广告牌的高度BC为_____________米