4.3 解直角三角形及其应用（4）

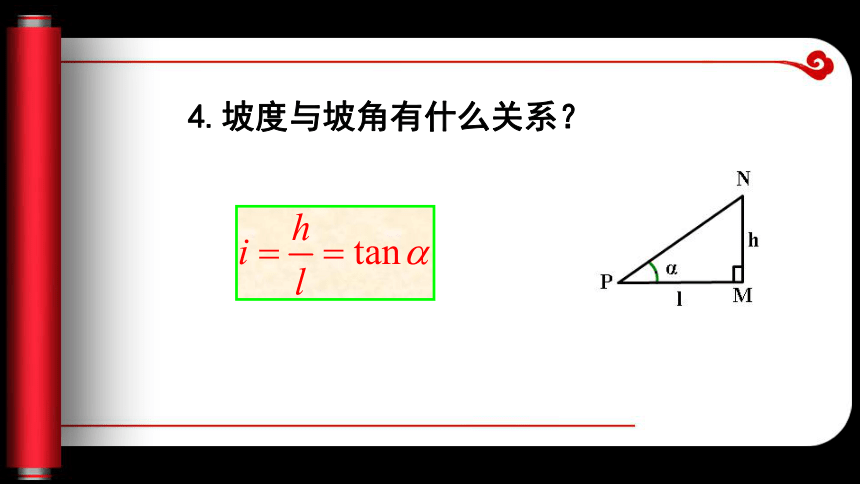
课件14张PPT。4.3 解直角三角形及其应用（4）湖南省新邵县酿溪中学王军旗1、我们登山时，平缓的坡感觉轻松，陡的坡感觉吃力，怎样用数量关系来衡量一个斜坡的倾斜程度呢？新课引言2、一个双休日，小芳和小花进行登山活动，活动路线如图所示，小芳沿着BA的方向上山，小花沿着CA的方向上山。想一想图中哪个山坡比较陡？你的依据是什么？ 1、坡度的定义：如图，从山坡脚下的点P走到点N时，升高的高度为h（即线段MN的长）与水平前进的距离（即线段PM的长）的比叫坡度，用字母i表示，即：i= ? 主题讲解主题一、坡度、坡角的概念 2、坡度常见的形式坡度一般写成 的形式。这种形式的作用：由此知道水平距离是垂直高度的m倍。 3.坡角：斜坡与水平面的夹角叫坡角。图中∠NPM4.坡度与坡角有什么关系？主题二、坡度坡角的初步应用 一山坡的坡度i=1:1.8,小刚从山坡脚下点P上坡走了240m到达点N，他上升了多少米（精确到0.1米）？这座山坡的坡角是多少度（精确到1′）试试看：解：用α表示坡角的大小，由于： ,∴α≈29 o3′ 在直角三角形PMN中，∠M=90 o, ∠P=29 o3′,PN=240m，sinα= MN=240sin29 o3′≈116.5(m)答：小刚上升了约116.5m,这座山坡的坡角约等于29 o3′你还有别的方法吗？例1有一拦水坝的横断面是等腰梯形，它的上底长为6m,下底长为10m,高为2 m,那么此拦水坝的坡度和坡角分别是多少？主题三、坡度、坡角的实际应用例2.拦洪坝的横断面为梯形ABCD,已知上底BC=5m,迎水坡度 =1: ,背水坡度 i=1:1,坡高为4m，求（1）下底AD的长（精确到m）,(2)迎水坡CD的长。（3）坡角α，β解:tan α=1: ∴ α=30 o
CD=2CE=2 ×4=8m，由CE:DE=1: ,DE= CE=4
Rt △BFA中，tanA=1:1, ∴ ∠B=45 o,AF=BF=EC=4m. ∴AD=DE+EF+FA=DE+CB+FA=4 +5+4=9+4如图，水坝横断面为梯形，梯形上底长3米，高4米，又水坝迎水坡、背水坡坡度分别为1： ，和1：1求水坝横断面积。（结果用根号表示）。变式练习： 小结 解坡度问题，关键是要知道坡度和坡角的概念及坡度坡角的关系。利用坡度的概念借助三角函数就可以轻松的求解。作业：P121 B 补充作业.沿水库拦水坝的背水坡将坝顶加宽2m,坡度由原来的1：2改为1：2.5，已知坝面高6米，坝长50米，（1）求加宽部分横断面AFEB的面积。（2）完成这一个工程需要多少方土？