第四章 锐角三角函数复习（1）

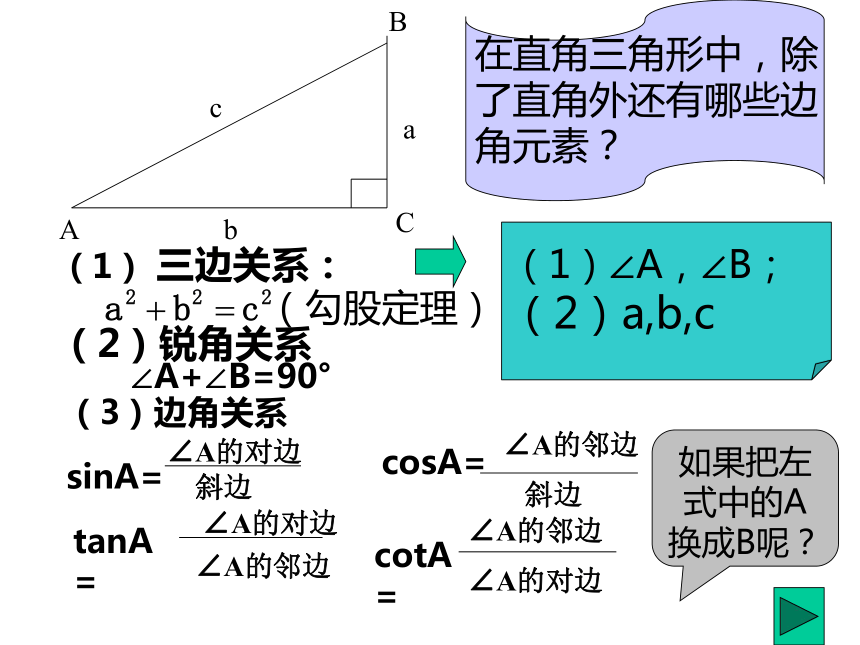
课件16张PPT。在直角三角形中，除
了直角外还有哪些边
角元素？ABCbac（1）∠A，∠B；
（2）a,b,c（1） 三边关系：（勾股定理）（2）锐角关系∠A+∠B=90°（3）边角关系sinA=∠A的对边斜边cosA=∠A的邻边斜边tanA=∠A的对边∠A的邻边cotA=∠A的邻边∠A的对边如果把左式中的A换成B呢？解直角三角形由直角三角形中除直角外的已知元素，求出
所有未知元素的过程利用三边的关系，锐角的关系，边角的关系，
知道其中的2个元素（至少有1个是边，）就可以
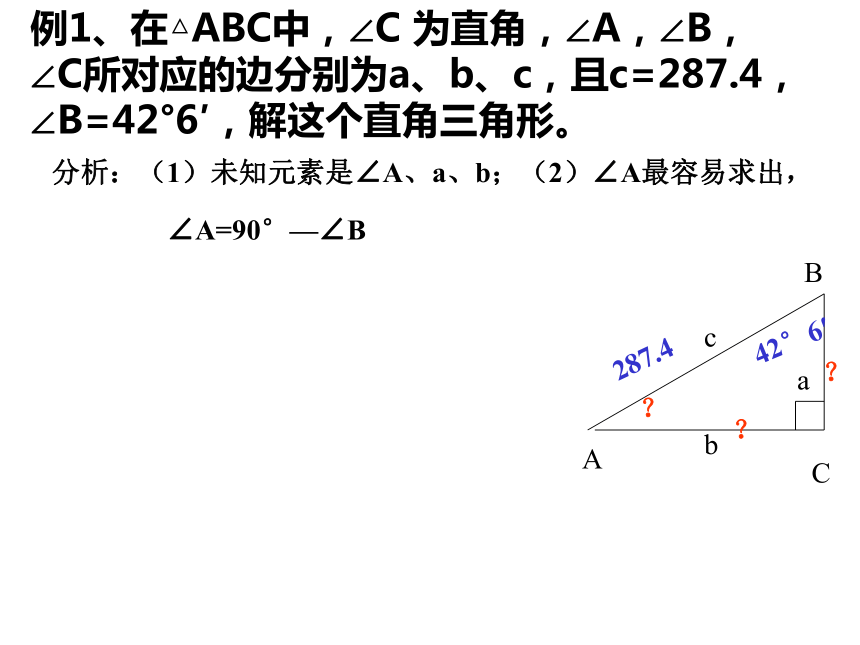
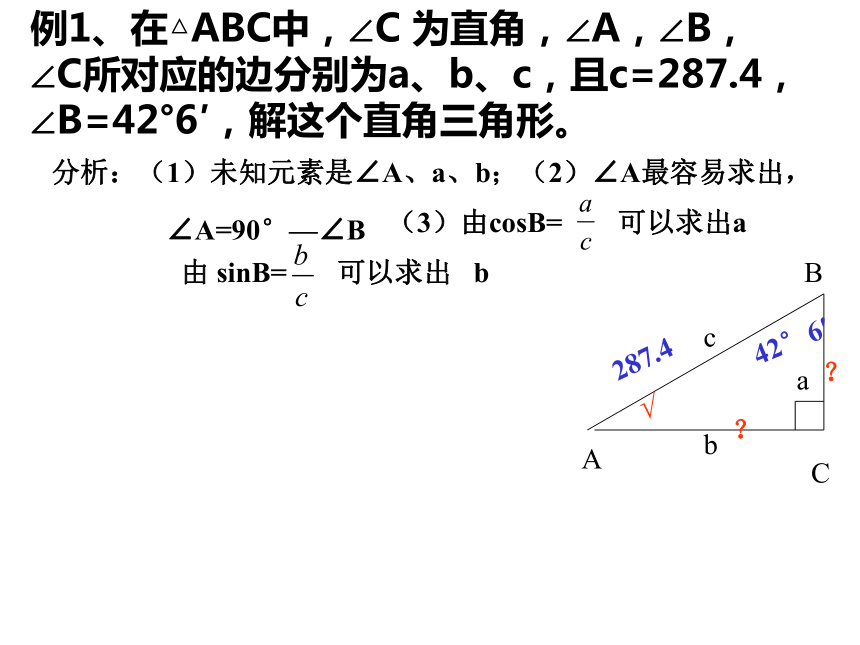
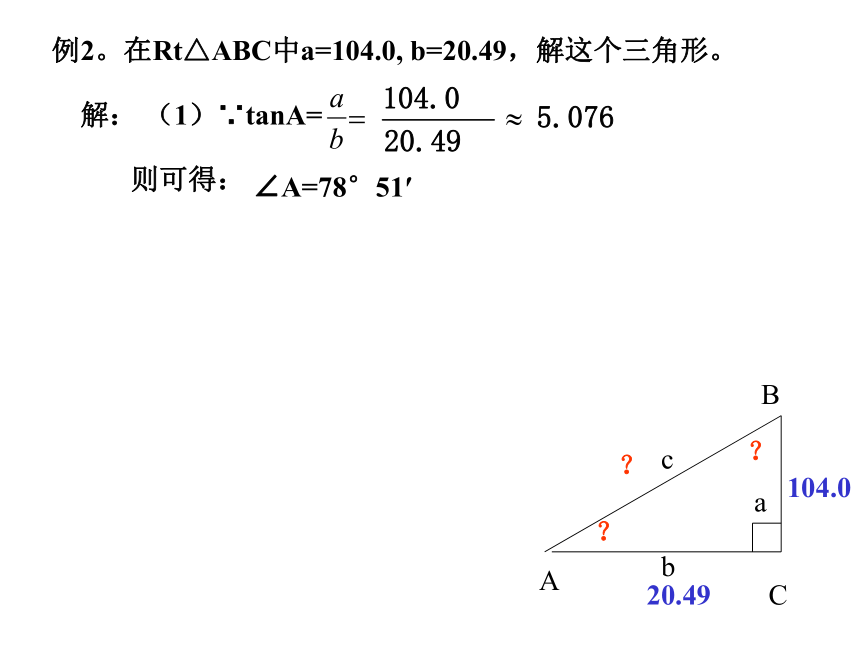
求出其余的3个元素。例1、在△ABC中，∠C 为直角，∠A，∠B，∠C所对应的边分别为a、b、c，且c=287.4，∠B=42°6′，解这个直角三角形。分析：（1）未知元素是∠A、a、b；（2）∠A最容易求出，∠A=90°—∠B287.442°6′？？？例1、在△ABC中，∠C 为直角，∠A，∠B，∠C所对应的边分别为a、b、c，且c=287.4，∠B=42°6′，解这个直角三角形。分析：（1）未知元素是∠A、a、b；（2）∠A最容易求出，∠A=90°—∠B可以求出a287.442°6′√？？例1、在△ABC中，∠C 为直角，∠A，∠B，∠C所对应的边分别为a、b、c，且c=287.4，∠B=42°6′，解这个直角三角形。分析：（1）未知元素是∠A、a、b；（2）∠A最容易求出，∠A=90°—∠B可以求出a解：（1）∠A=90°—42°6′（2）∵cosB=∴a=ccosB=287.4×cos42°6′=287.4×0.7420≈213.3（3）∵sinB=∴b=csinB=287.4×sin42°6′=287.4×0.67.4≈192.7287.442°6′√√√=47°54′例2。在Rt△ABC中a=104.0, b=20.49，解这个三角形。解： （1）∵tanA=则可得：∠A=78°51′104.020.49？？？例2。在Rt△ABC中a=104.0, b=20.49，解这个三角形。解： （1）∵tanA=则可得：∠A=78°51′（2）∠B=90°—78°51′=11°19′（3）∵sinA=∴c=104.020.49？？78°51′解直角三角形的思考方法是：有斜（斜边）用
弦（正、余弦），无斜用切（正、余切）；
宁乘勿除，尽量采用原始数据，以图辅助，
启迪思维。意思：当已知或求解中有斜边时，就用正弦
或余弦；无斜边时，就用正切或余切；当所求
的元素既可用乘法又可用除法时，则用乘法，
不用除法；既可由已知数据又可用中间数据求
得时，则取原始数据，避免用中间数据。课堂练习：在Rt△ABC中,∠C=90°,解这个直角三角形。CBA课堂练习1。在Rt△ABC中，（1）如果已知∠A，c,则a= b= ∠B= （2）如果已知a, ∠B,则 b= c= ∠A=（3）如果已知∠A，b,则a= c= ∠B=（4）如果已知a,b,则 c= ∠A= ∠B=课堂练习1。在Rt△ABC中，（1）如果已知∠A，c,则a= b= ∠B= （2）如果已知a, ∠B,则 b= c= ∠A=（3）如果已知∠A，b,则a= c= ∠B=（4）如果已知a,b,则 c= ∠A= ∠B=CBAabc课堂练习1。在Rt△ABC中，（1）如果已知∠A，c,则a= b= ∠B= （2）如果已知a, ∠B,则 b= c= ∠A=（3）如果已知∠A，b,则a= c= ∠B=（4）如果已知a,b,则 c= ∠A= ∠B=CBAabc课堂练习1。在Rt△ABC中，（1）如果已知∠A，c,则a= b= ∠B= （2）如果已知a, ∠B,则 b= c= ∠A=（3）如果已知∠A，b,则a= c= ∠B=（4）如果已知a,b,则 c= ∠A= ∠B=CBAabc直角三角形的解法：①已知一条直角边和一个锐角（如a, ∠A）∠B=90°—∠A，或②已知斜边和一个锐角（如c, ∠A），其解法为：∠B=90°—∠A，或③已知两直角边（a,b）其解法为：由得出∠A，∠B=90°—∠A④已知斜边和一直角边（如c,a ），其解法为：由得出∠A，∠B=90°—∠A（A、B）
一、填空
1、若tanA=2，则cot（90°-A）=_______
2、α为锐角，且tan α=1，则α=____，
cos α=_____
3、在Rt△ABC中，∠C=90°，AB=13，AC=12
则sinA=_____，cotA=_____
4、tan42°tan45°tan48°=_____
二、计算
1、cos245+tan60°sin60°
2、2sin30°+tan60°cos30°-3cot 260°+sin90°C、D
一、填空
1、已知α为锐角，且tanα= ，则α=____
2、求值tan1°tan2°tan3° tan87°tan88°
tan89°=_____
3、设θ为锐角，且x2+3x+2sin θ=0d的两根之
差为 ，则θ=_____
4、已知sin2 α= ，则α=_____
二、计算
tan60°+cot45°4sin30°