江苏省淮安市南陈集中学2010-2011学年高一第一学期期中教学调研数学试题
文档属性
| 名称 | 江苏省淮安市南陈集中学2010-2011学年高一第一学期期中教学调研数学试题 |

|
|
| 格式 | rar | ||
| 文件大小 | 153.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-24 00:00:00 | ||
图片预览




文档简介
淮安市南陈集中学2010-2011学年度第一学期期中调研
高一数学试题
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应的位置上.
1、设集合,,则 ★
2、 ★
3、若函数的定义域为,则其值域为 ★
4、若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,
参考数据如下表:
f(1)=- 2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.438)=0.165
f(1.4065)=-0.052
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ★
5、在映射,,且,则与A中的元素(-1,2)对应的B中的元素为 ★
6、下列四组函数中,表示同一函数的是 ★
7、函数的递增区间为 ★
8、 ★ .
(1) (2) (3) (4)
9、若,则 ★
10、 已知函数,则的定义域为 ★
11、设偶函数f(x)的定义域为R,当x时,f(x)是增函数,则f(-2),f(),f(-3)的大小关系是 ★
12、有一块边长为a的正方形铁皮,将其四个角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,写出体积V以x为自变量的函数是 ★
13、若方程有解,则a的取值范围是 ★
14、给出下列五个命题:
①函数是偶函数,但不是奇函数.
②函数y=的单调增区间为(1,).
③函数的值域是,则函数的值域为.
④ 设函数定义域为R且满足则它的图象关于 轴对称.
⑤一条曲线和直线的公共点个数是,则的值不可能是1.
其中正确的命题序号是 ★
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
记函数的定义域为集合M,函数的定义域为集合N.求:
(1)集合M,N;
(2)集合,。
16、 (本小题满分14分)
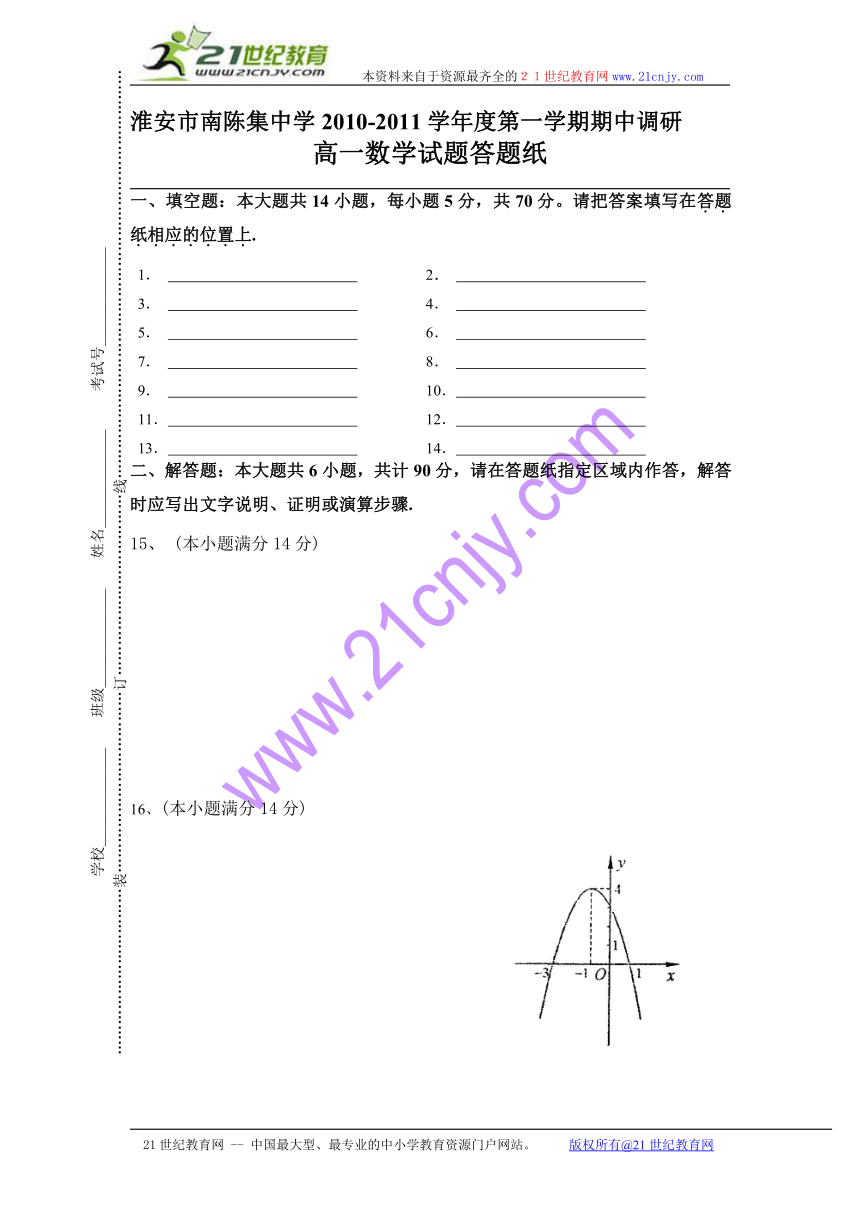
如右图是一个二次函数y=f(x)的图象.
(1)写出函数f(x)的表达式.
(2)求使函数值取非负值的x的集合;
(3)试判断f(-4)·f(-1),f(-1)·f(2)的正负。
17、(本小题满分15分)
若是定义在上的增函数,且
(1)求的值;
(2)若,解不等式
18、 (本小题满分15分)
设函数.
(1)求它的定义域;
(2)判断它的奇偶性;
(3)判断它的单调性并证明 。
19、(本题满分16分)
某车站有快慢两种车,始发站距终点站为,慢车匀速行驶到终点需,快车比慢车晚发车且匀速行驶以后到达终点站,设慢车行驶时间为,快、慢车行驶的路程分别为
(1)分别写出的函数关系式并写出定义域;在同一坐标系中作出的图象。
(2)两车中途何时相遇,此时距离始发站多远?
20、 (本小题满分16分)
探究函数,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
x
…
0.5
1
1.5
1.7
1.9
2
2.1
2.2
2.3
3
4
5
7
…
y
…
8.5
5
4.17
4.05
4.005
4
4.005
4.102
4.24
4.3
5
5.8
7.57
…
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
(3)试用定义证明,(x>0)在区间(0,2)上递减;
(4)函数,(a>0, 且a≠1)有最值吗?是最大值还是最小值?此时x为何值?(只写结果,不要求写过程).
淮安市南陈集中学2010-2011学年度第一学期期中调研
高一数学试题答题纸
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题纸相应的位置上.
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
二、解答题:本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
16、(本小题满分14分)
17、(本小题满分15分)
18、(本小题满分15分)
19、(本小题满分16分)
20、 (本小题满分16分)
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
淮安市南陈集中学2010-2011学年度第一学期期中调研
高一数学试题参考答案及评分标准
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应的位置上.
1. 2. 3. 4. 1.4 5 6. 7.(右端点可以闭) 8. 9. 10. 11. 12. 13. 14.
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
解:(1)由得 ……2分
由得或 ……4分
(2)
……8分
……11分
……14分
16、(本小题满分14分)
解: (1) 由题图可设:
……6分
由得
使f(x)值为非负值的x的集合是{x│-3≤x≤1}; ……10分
f(-4)·f?(-1)<0, ……12分
f(-1)·f(2)<0. ……14分
17、(本小题满分15分)
解:(1)令得 ……3分
(2)令,得
……6分
由得
……10分
……15分
18、(本小题满分15分
解:(1)由得
的定义域为: ……4分
(2)的定义域为:
为奇函数 ……8分
(3)
设,则
在上单调增 同理可证:在上单调增 ……13分
在,上为增函数 ……15分
19、(本小题满分16分
解:(1)慢车的速度为 ……1分
快车速度为 ……2分
……6分
…… 8分
图象为:
……10分
(2)显然时两车不可能相遇,当时,
……14分
答:两车当时相遇,此时距起点约 ……16分
20、 (本小题满分16分)
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
解:(1) (2,+∞) (左端点可以闭) ……2分
(2)x=2时,ymin=4 ……4分
(3) 设0f(x1)- f(x2)=
= (#)
∵0∴(#)式>0即f(x1)- f(x2)>0 ∴f(x1)> f(x2)
∴f(x)在区间(0,2)上递减。 ……10分
(4) 有最小值4
时,有最小值,此时x= 2。 ……13分
时,有最大值,此时x= 2。 ……16分
高一数学试题
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应的位置上.
1、设集合,,则 ★
2、 ★
3、若函数的定义域为,则其值域为 ★
4、若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法逐次计算,
参考数据如下表:
f(1)=- 2
f(1.5)=0.625
f(1.25)=-0.984
f(1.375)=-0.260
f(1.438)=0.165
f(1.4065)=-0.052
那么方程x3+x2-2x-2=0的一个近似根(精确到0.1)为 ★
5、在映射,,且,则与A中的元素(-1,2)对应的B中的元素为 ★
6、下列四组函数中,表示同一函数的是 ★
7、函数的递增区间为 ★
8、 ★ .
(1) (2) (3) (4)
9、若,则 ★
10、 已知函数,则的定义域为 ★
11、设偶函数f(x)的定义域为R,当x时,f(x)是增函数,则f(-2),f(),f(-3)的大小关系是 ★
12、有一块边长为a的正方形铁皮,将其四个角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,写出体积V以x为自变量的函数是 ★
13、若方程有解,则a的取值范围是 ★
14、给出下列五个命题:
①函数是偶函数,但不是奇函数.
②函数y=的单调增区间为(1,).
③函数的值域是,则函数的值域为.
④ 设函数定义域为R且满足则它的图象关于 轴对称.
⑤一条曲线和直线的公共点个数是,则的值不可能是1.
其中正确的命题序号是 ★
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
记函数的定义域为集合M,函数的定义域为集合N.求:
(1)集合M,N;
(2)集合,。
16、 (本小题满分14分)
如右图是一个二次函数y=f(x)的图象.
(1)写出函数f(x)的表达式.
(2)求使函数值取非负值的x的集合;
(3)试判断f(-4)·f(-1),f(-1)·f(2)的正负。
17、(本小题满分15分)
若是定义在上的增函数,且
(1)求的值;
(2)若,解不等式
18、 (本小题满分15分)
设函数.
(1)求它的定义域;
(2)判断它的奇偶性;
(3)判断它的单调性并证明 。
19、(本题满分16分)
某车站有快慢两种车,始发站距终点站为,慢车匀速行驶到终点需,快车比慢车晚发车且匀速行驶以后到达终点站,设慢车行驶时间为,快、慢车行驶的路程分别为
(1)分别写出的函数关系式并写出定义域;在同一坐标系中作出的图象。
(2)两车中途何时相遇,此时距离始发站多远?
20、 (本小题满分16分)
探究函数,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
x
…
0.5
1
1.5
1.7
1.9
2
2.1
2.2
2.3
3
4
5
7
…
y
…
8.5
5
4.17
4.05
4.005
4
4.005
4.102
4.24
4.3
5
5.8
7.57
…
请观察表中y值随x值变化的特点,完成下列问题:
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
(3)试用定义证明,(x>0)在区间(0,2)上递减;
(4)函数,(a>0, 且a≠1)有最值吗?是最大值还是最小值?此时x为何值?(只写结果,不要求写过程).
淮安市南陈集中学2010-2011学年度第一学期期中调研
高一数学试题答题纸
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题纸相应的位置上.
1. 2.
3. 4.
5. 6.
7. 8.
9. 10.
11. 12.
13. 14.
二、解答题:本大题共6小题,共计90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
16、(本小题满分14分)
17、(本小题满分15分)
18、(本小题满分15分)
19、(本小题满分16分)
20、 (本小题满分16分)
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
淮安市南陈集中学2010-2011学年度第一学期期中调研
高一数学试题参考答案及评分标准
一、填空题:本大题共14小题,每小题5分,共70分。请把答案填写在答题卡相应的位置上.
1. 2. 3. 4. 1.4 5 6. 7.(右端点可以闭) 8. 9. 10. 11. 12. 13. 14.
二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.
15、 (本小题满分14分)
解:(1)由得 ……2分
由得或 ……4分
(2)
……8分
……11分
……14分
16、(本小题满分14分)
解: (1) 由题图可设:
……6分
由得
使f(x)值为非负值的x的集合是{x│-3≤x≤1}; ……10分
f(-4)·f?(-1)<0, ……12分
f(-1)·f(2)<0. ……14分
17、(本小题满分15分)
解:(1)令得 ……3分
(2)令,得
……6分
由得
……10分
……15分
18、(本小题满分15分
解:(1)由得
的定义域为: ……4分
(2)的定义域为:
为奇函数 ……8分
(3)
设,则
在上单调增 同理可证:在上单调增 ……13分
在,上为增函数 ……15分
19、(本小题满分16分
解:(1)慢车的速度为 ……1分
快车速度为 ……2分
……6分
…… 8分
图象为:
……10分
(2)显然时两车不可能相遇,当时,
……14分
答:两车当时相遇,此时距起点约 ……16分
20、 (本小题满分16分)
(1)若函数,(x>0)在区间(0,2)上递减,则在 上递增;
(2)当x= 时,,(x>0)的最小值为 ;
解:(1) (2,+∞) (左端点可以闭) ……2分
(2)x=2时,ymin=4 ……4分
(3) 设0
= (#)
∵0
∴f(x)在区间(0,2)上递减。 ……10分
(4) 有最小值4
时,有最小值,此时x= 2。 ……13分
时,有最大值,此时x= 2。 ……16分
同课章节目录
