圆周角1学案

圆周角和圆心角的关系（第一课时）
学习目标:
　（1）理解圆周角的概念,掌握圆周角的两个特征、定理的内容及简单应用；
　（2）渗透由“特殊到一般”，由“一般到特殊”的数学思想方法以及转化、分类、归纳等数学思想；
学习重点:
圆周角的概念和圆周角定理
学习难点:
圆周角定理的证明中由“特殊到一般”的数学思想方法和完全归纳法的数学思想．
学习过程:
（一）复习填空，导入新知：
顶点在圆心的角叫________,圆心角的度数_______它所对弧的度数。
（二）自主探究，学习新知：
1、圆周角定义： 。
圆周角必须具备两个条件：①顶点在________，②两边_________（缺一不可）课本练习P123T1，自主完成后统一纠正。
2、圆周角定理
学生动手：请画出下列各图中劣弧AB所对的圆周角，并度量其度数。
弧AB为 弧AB为 弧AB为
①分别写出劣弧AB所对的圆心角度数：图1____图2_____图3_____
②度量劣弧AB所对的圆周角的度数：图1_____图2_____图3______
③比较两个角的度数，你从特例中发现了什么？
学生猜想：
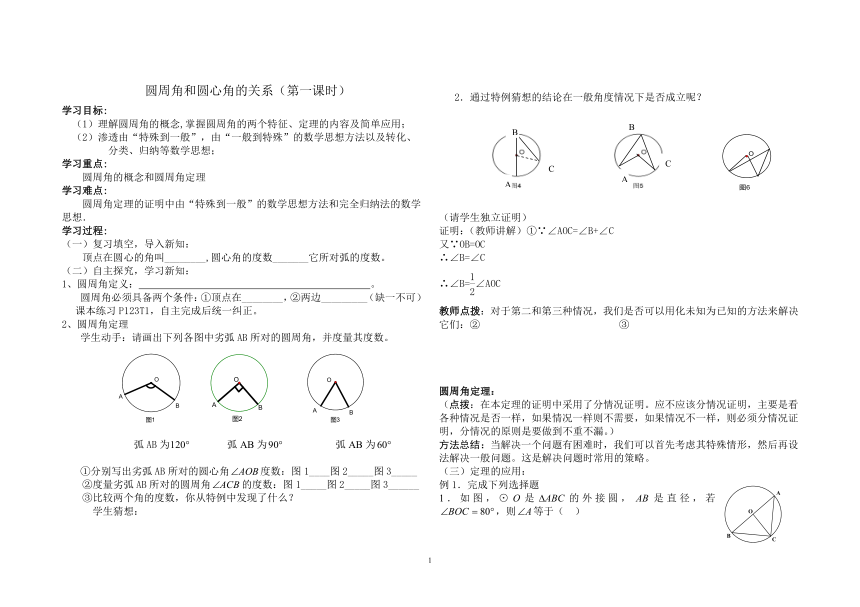
2．通过特例猜想的结论在一般角度情况下是否成立呢？
（请学生独立证明）
证明：（教师讲解）①∵∠AOC=∠B+∠C
又∵OB=OC
∴∠B=∠C
∴∠B=!异常的公式结尾∠AOC
教师点拨：对于第二和第三种情况，我们是否可以用化未知为已知的方法来解决它们：② ③
圆周角定理：
（点拨：在本定理的证明中采用了分情况证明。应不应该分情况证明，主要是看各种情况是否一样，如果情况一样则不需要，如果情况不一样，则必须分情况证明，分情况的原则是要做到不重不漏。）
方法总结：当解决一个问题有困难时，我们可以首先考虑其特殊情形，然后再设法解决一般问题。这是解决问题时常用的策略。
（三）定理的应用：
例1．完成下列选择题
1．如图，⊙是的外接圆，是直径，若 ，则等于（ ）
A．60 B．50 C．40 D．30
2．如图，内接于，若，则的大小为（ ）
A． 　　　B．　　 C．　　　D．
3．如图，已知CD为⊙O的直径，过点D的弦DE平行
于半径OA，若∠D的度数是50°，则∠C的度数是：
A．25° B．40° C．30° D．50°
例2．如图，OA、OB、OC都是圆O的半径，∠ AOB=2∠ BOC．求证：∠ACB=2∠ BAC
拓展：已知⊙O中的弦AB长等于半径，求弦AB所对的圆心角和圆周角的度数．
练习：一条弦分圆为1：4两部分，求这条弦所对的圆周角的度数？
三、课堂小结：
四、作业：课本习题P124T2，3
体会：
A
C
A
B
O
C
B
B
C
A
PAGE
2