15.22旋转的特征
图片预览





文档简介
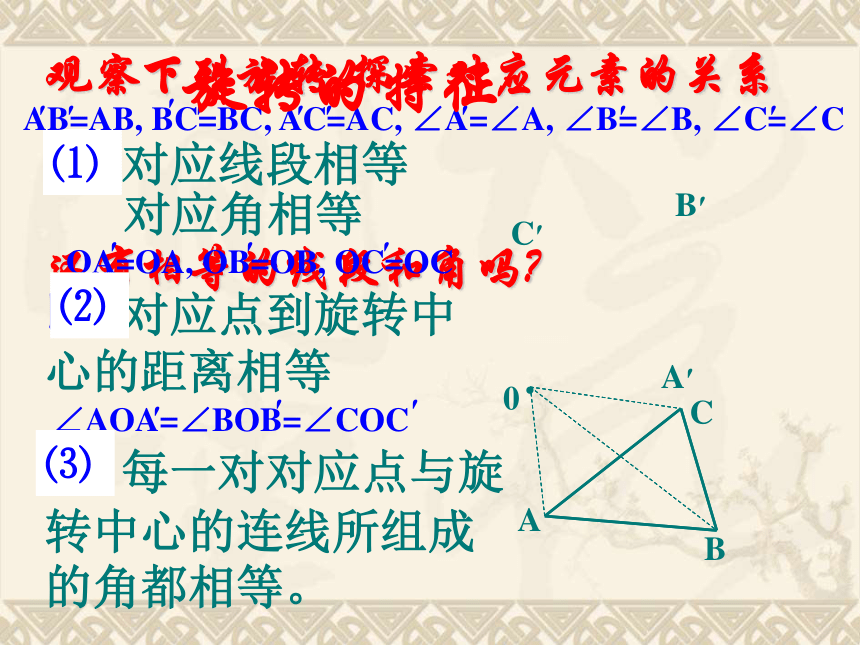
课件24张PPT。15.2.2旋转的特征黔江民族中学 杨 霞知识回顾⑴旋转的概念:在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动⑵旋转的要素:旋转不改变图形大小和形状,只改变图形的位置.叫做图形的旋转,简称旋转.旋转中心.旋转方向和旋转角.⑶旋转的特征: 1.下列现象中属于旋转的有 ( )个.
①地下水位逐年下降;②传送带的移动;③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
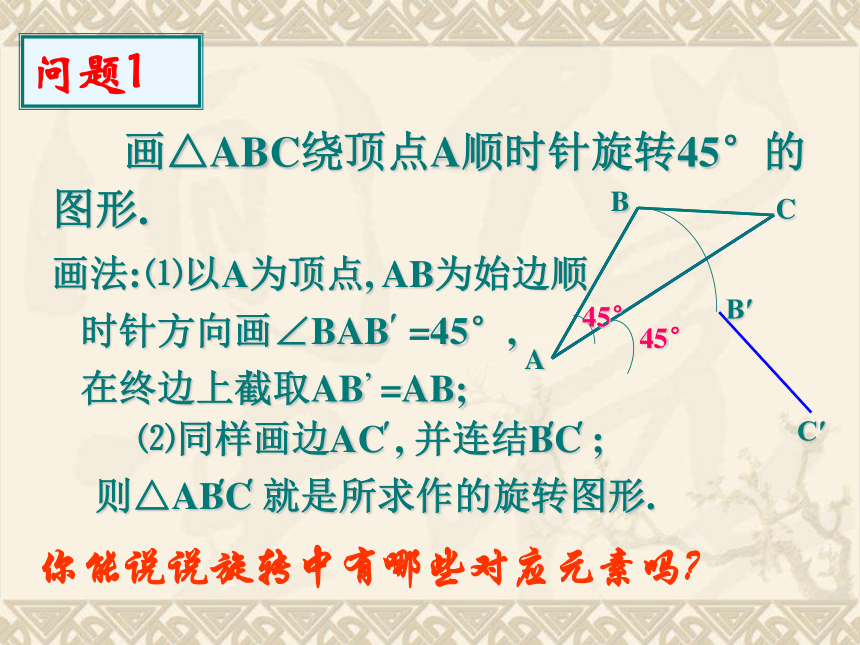
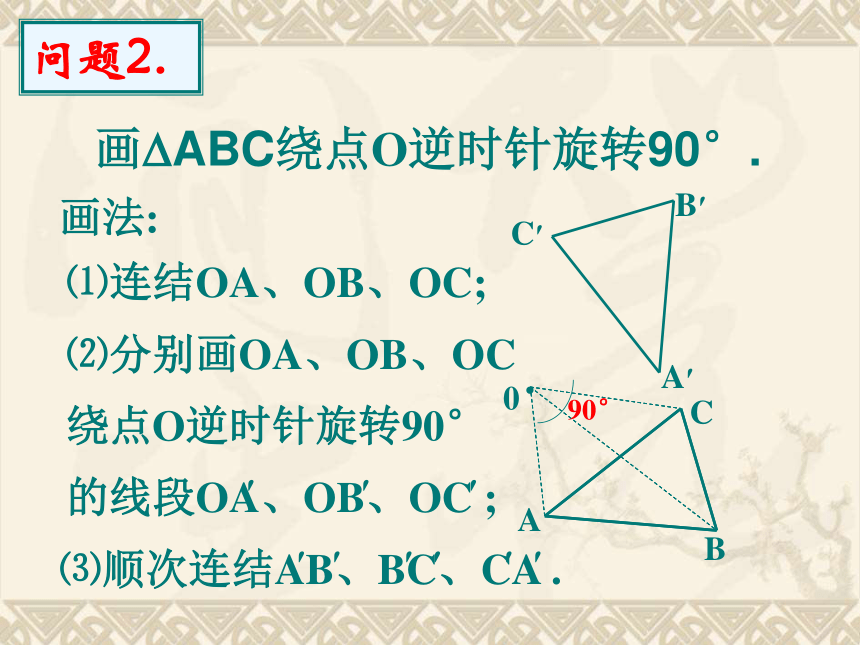
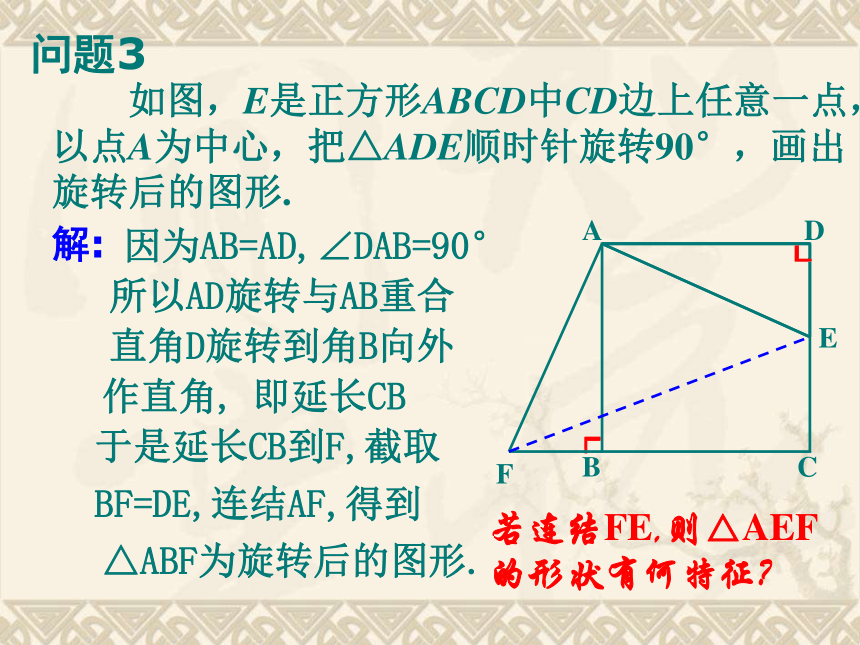
A.2 B.3 C.4 D.5 基本练习√××√√√C 2.如图,利用杠杆撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?基本练习答:杠杆旋转的中心是支点O,旋转角是∠AOA 和∠BOB.′′ 3.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它可以由其基本练习中一瓣经过 次旋转4而得到, 每次旋转的角度分别是72°, 144°216°, 288°即: 对应线段相等观察下列旋转,探索对应元素的关系0ABC·A′B′C′⑴对应角相等还有相等的线段和角吗?即: 对应点到旋转中心的距离相等⑵即: 每一对对应点与旋转中心的连线所组成的角都相等。⑶旋转的特征 画△ABC绕顶点A顺时针旋转45°的图形.ABCB′C′画法:45°⑴以A为顶点, AB为始边顺时针方向画∠BAB =45°,′在终边上截取AB’ =AB;′⑵同样画边AC , 并连结BC ;′′′则△ABC 就是所求作的旋转图形.′′45°你能说说旋转中有哪些对应元素吗?问题1画?ABC绕点O逆时针旋转90°.问题2.0ABC·A′B′C′90°画法:⑴连结OA、OB、OC;⑵分别画OA、OB、OC绕点O逆时针旋转90°的线段OA、OB、OC ;′′′⑶顺次连结AB、BC、CA .′′′′′′ 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.问题3ABCD解:因为AB=AD,∠DAB=90°所以AD旋转与AB重合┖直角D旋转到角B向外作直角, ┖即延长CB 于是延长CB到F,截取 EFBF=DE,连结AF,得到 △ABF为旋转后的图形.若连结FE,则△AEF的形状有何特征?问题4如图中, 正方形ABCD和正方形AKLM试用旋转的思想说明线段BK和DM的关系解:由正方形得:AB=AD, AK=AM且∠ BAD=∠KAM =90°∴△ABK绕点A逆时针旋转90°恰与△ADM重合∴对应线段BK和DM相等且垂直.课堂反馈 如图,点D是等边△ABC内一点, 若将△ABD点AABCD旋转到△ACP, 则旋转中心是 ; 旋转角是= 度; ∠BAC60则△ADP是 三角形.等边⑵已知AD=4, BD=3, 又连结CD, 且CD=5, 则△DCP是 三角形; ∠ADB= 度.直角150P ⑴若连结DP,435A? B? C? 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案. (1)作OD?OA,在OD上截取OA? =OA,OB? = OB;(2) 连结OC;(3) 作OF?OC,在OF上截取OC? =OC; (4) 连结A? C? 、B? C?.┓┓ 如图,即可作出“小旗子”按要求旋转后的图案.解:例2DF 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点? 请在图中画出并说明理由;(2)旋转了多少度? (3)说出线段AF与BE的关系?旋转中心在对应点连线的垂直平分线上,如图点O即为所求如图∠AOD即为旋转角,顺时针旋转90 °例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合(3)说出线段AF与BE的关系?解:相等且互相垂直,证明如下:
∵ ?ABE旋转后能与?ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE例3 1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:AECBD(1)旋转中心是_____,旋转的度数是____ (2)若已知∠DCB=200,则∠CDB=_______, ∠AEC=____, ∠BAE=____(3)如果连结DE,那么
△DCE是________三角形。点C90°115°90°等腰直角115°练习A、45°,90° B、90°,45° C、60°,30° D、30°,60°A2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上76页练习2)A’B’如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?思考题如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。你有什么收获?课堂小结旋转的特征⑵对应角相等⑶⑴对应线段相等对应点到旋转中心的距离相等,并且每一对对应点与旋转中心的连线所组成的角都相等。
作业: 1.必做题:教科书第75页第3题 第79页第3题 作业(选做题)ABCDOMN已知正方形ABCD的边长为2, 对角线相交于O,另有正方形OEFG绕O旋转任意角度,OE、OG分别交AB、BC于M、N⑴观察△OCN和△OBM的关系,求CN+AM;⑵求四边形OMBN的面积.EFG同学们,再见!
①地下水位逐年下降;②传送带的移动;③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
A.2 B.3 C.4 D.5 基本练习√××√√√C 2.如图,利用杠杆撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?基本练习答:杠杆旋转的中心是支点O,旋转角是∠AOA 和∠BOB.′′ 3.香港特别行政区区旗中央的紫荆花图案由5个相同的花瓣组成,它可以由其基本练习中一瓣经过 次旋转4而得到, 每次旋转的角度分别是72°, 144°216°, 288°即: 对应线段相等观察下列旋转,探索对应元素的关系0ABC·A′B′C′⑴对应角相等还有相等的线段和角吗?即: 对应点到旋转中心的距离相等⑵即: 每一对对应点与旋转中心的连线所组成的角都相等。⑶旋转的特征 画△ABC绕顶点A顺时针旋转45°的图形.ABCB′C′画法:45°⑴以A为顶点, AB为始边顺时针方向画∠BAB =45°,′在终边上截取AB’ =AB;′⑵同样画边AC , 并连结BC ;′′′则△ABC 就是所求作的旋转图形.′′45°你能说说旋转中有哪些对应元素吗?问题1画?ABC绕点O逆时针旋转90°.问题2.0ABC·A′B′C′90°画法:⑴连结OA、OB、OC;⑵分别画OA、OB、OC绕点O逆时针旋转90°的线段OA、OB、OC ;′′′⑶顺次连结AB、BC、CA .′′′′′′ 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.问题3ABCD解:因为AB=AD,∠DAB=90°所以AD旋转与AB重合┖直角D旋转到角B向外作直角, ┖即延长CB 于是延长CB到F,截取 EFBF=DE,连结AF,得到 △ABF为旋转后的图形.若连结FE,则△AEF的形状有何特征?问题4如图中, 正方形ABCD和正方形AKLM试用旋转的思想说明线段BK和DM的关系解:由正方形得:AB=AD, AK=AM且∠ BAD=∠KAM =90°∴△ABK绕点A逆时针旋转90°恰与△ADM重合∴对应线段BK和DM相等且垂直.课堂反馈 如图,点D是等边△ABC内一点, 若将△ABD点AABCD旋转到△ACP, 则旋转中心是 ; 旋转角是= 度; ∠BAC60则△ADP是 三角形.等边⑵已知AD=4, BD=3, 又连结CD, 且CD=5, 则△DCP是 三角形; ∠ADB= 度.直角150P ⑴若连结DP,435A? B? C? 在方格子纸上作出“小旗子”绕点O按顺时针方向旋转90°后的图案. (1)作OD?OA,在OD上截取OA? =OA,OB? = OB;(2) 连结OC;(3) 作OF?OC,在OF上截取OC? =OC; (4) 连结A? C? 、B? C?.┓┓ 如图,即可作出“小旗子”按要求旋转后的图案.解:例2DF 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合O(1)旋转中心是哪一点? 请在图中画出并说明理由;(2)旋转了多少度? (3)说出线段AF与BE的关系?旋转中心在对应点连线的垂直平分线上,如图点O即为所求如图∠AOD即为旋转角,顺时针旋转90 °例3 如图,在正方形ABCD中, ?ABE旋转后能与?ADF重合(3)说出线段AF与BE的关系?解:相等且互相垂直,证明如下:
∵ ?ABE旋转后能与?ADF重合
∴AF=BE且∠1=∠2,
又∠2+∠3=90°
∴∠1+∠3=90°
∴∠AOE=90°即AF⊥BE
∴AF=BE 且AF⊥BE例3 1、如图,△ABC是等腰直角三角形,D是AB上一点,△CBD经旋转后到达△CAE的位置。问:AECBD(1)旋转中心是_____,旋转的度数是____ (2)若已知∠DCB=200,则∠CDB=_______, ∠AEC=____, ∠BAE=____(3)如果连结DE,那么
△DCE是________三角形。点C90°115°90°等腰直角115°练习A、45°,90° B、90°,45° C、60°,30° D、30°,60°A2、 如图1,ΔABC和ΔADE都是等腰直角三角形,∠ACB和∠ADE都是直角,点C在AE上,ΔABC绕着A点经过逆时针旋转后能够与ΔADE重合得到图1,再将图1作为“基本图形”绕着A点经过逆时针连续旋转得到图2;两次旋转的角度分别为( ).3、画出△ABC绕点C逆时针旋转90°后的图形
(书本上76页练习2)A’B’如图是一个直角三角形的苗圃,有正方形花坛和两块直角三角形的草皮组成,如果两个直角三角形的两条斜边长分别为3米和6米,问草皮的面积是多少?思考题如图 :通过旋转图形,我们可以把两个直角三角形拼结成一个直角三角形,而这个直角三角形的两条直角边正好是3米和6米。你有什么收获?课堂小结旋转的特征⑵对应角相等⑶⑴对应线段相等对应点到旋转中心的距离相等,并且每一对对应点与旋转中心的连线所组成的角都相等。
作业: 1.必做题:教科书第75页第3题 第79页第3题 作业(选做题)ABCDOMN已知正方形ABCD的边长为2, 对角线相交于O,另有正方形OEFG绕O旋转任意角度,OE、OG分别交AB、BC于M、N⑴观察△OCN和△OBM的关系,求CN+AM;⑵求四边形OMBN的面积.EFG同学们,再见!
