24.2.2直线与圆的位置关系
文档属性
| 名称 | 24.2.2直线与圆的位置关系 |
|
|
| 格式 | rar | ||
| 文件大小 | 40.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-26 21:25:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
24.2.2直线与圆有关的位置关系
第1课时
教学目标
(1)了解直线和圆的位置关系的有关概念.
(2)理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:
直线L和⊙O相交dr.
(3)理解切线的判定定理:理解切线的性质定理并熟练掌握以上内容解决一些实际问题.
复习点和圆的位置关系,引入直线和圆的位置关系,以直线和圆的位置关系中的d=r直线和圆相切,讲授切线的判定定理和性质定理.
重难点、关键
1.重点:切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目.
2.难点与关键:由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价.
教学过程
一、复习引入
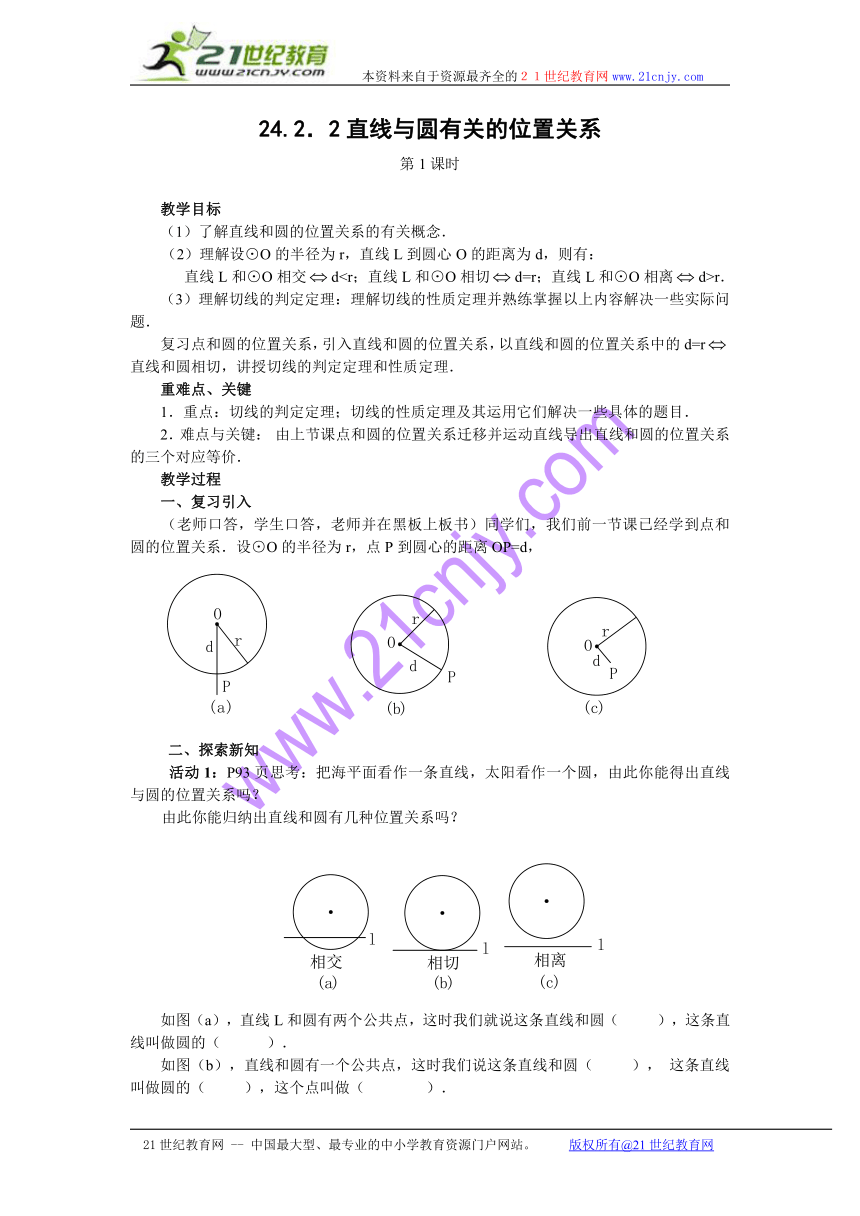
(老师口答,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
二、探索新知
活动1:P93页思考:把海平面看作一条直线,太阳看作一个圆,由此你能得出直线与圆的位置关系吗?
由此你能归纳出直线和圆有几种位置关系吗?
( http: / / )
如图(a),直线L和圆有两个公共点,这时我们就说这条直线和圆( ),这条直线叫做圆的( ).
如图(b),直线和圆有一个公共点,这时我们说这条直线和圆( ),这条直线叫做圆的( ),这个点叫做( ).
如图(c),直线和圆没有公共点,这时我们说这条直线和圆( ).
活动2:判断正误:
1、 直线与圆最多有两个公共点 。…………………( )
2、 若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
3、 若A、B是⊙O外两点, 则直线AB与⊙O相离。… … … … …( )
4、 若C为⊙O内一点,则过点C的直线与⊙O相交。( )
活动3:思考:如何判断直线与圆的位置关系?
老师点评直线L和⊙O相交d小结:直线与圆的位置关系(幻灯片14)
直线与圆的位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
活动4、练习1
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
3、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
练习2
1、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
切线的判定
一、复习引入:直线与圆的三中位置关系中,最重要的是直线与圆相切,本节课重点研究这一种位置关系。
在证明“直线与圆相切 d=r”,其实证明了“垂直于切线的直径必过切点”,反之“经过切点且垂直于切线的直线必过圆心”也同样成立。(板书以上两条切线的性质)
探讨:过圆心且过切点的直线,是否垂直于切线呢?
二、探索新知:
活动1、已知直线l 是⊙O的切线,切点为A,连接0A,你发现了什么?
(幻灯片3、幻灯片4)结论:圆的切线垂直于过切点的半径。
综合以上三条切线的性质,可总结为:一条直线若满足①过圆心,②过切点,③垂直于切线这三条中的任意两条,就必然满足第三条。(板书)
活动2、画⊙O及半径OA,画一条直线l过半径OA的外端点,且垂直于OA。你发现直线l与⊙O有怎样的位置关系?为什么?
(幻灯片5)
因为d=r直线L和⊙O相切,这里的d是圆心O到直线L的距离,即垂直,并由d=r就可得到L经过半径r的外端,即半径OA的A点,因此,很明显的,我们可以得到切线的判定定理:(幻灯片6)
经过半径的外端并且垂直于这条半径的直线是圆的切线.(板书)
判断下图直线L是否是⊙O的切线?并说明为什么。(幻灯片7)
例1(P95例1)直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.(幻灯片8)略
(学生分组讨论):根据上面的判定定理,如果你要证明一条直线是⊙O的切线,你应该如何证明?
(老师点评):应分为两步:(1)说明这个点是圆上的点,(2)过这点的半径垂直于直线.
练习:1.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC, ∠A=30.求证:直线AB是⊙O的切线. (幻灯片9)
小结:辅助线:有点连圆心,证垂直
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系, 并证明你的结论。(幻灯片10)
小结:辅助线:无点做垂线,证相等
例2、小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的直径(锅边所形成的圆的直径),而小红家只有一把长20cm 的直尺,根本不够长,怎么办呢 小红想了想,采取以下方法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出墙的直径,请你利用下图,说明她这样做的道理.
(幻灯片11)
练习:(幻灯片12、幻灯片13)
三、归纳小结:1、切线的性质定理;2、切线的三条判定定理;3、常见辅助线。
四、布置作业:P101习题24.2复习巩固4、5;
五、课后反思:本节课内容较多,由于安排得当,课堂完成情况较好;但是从作业中反映出的问题看,仍然存在着书写证明过程不规范、不严谨的问题。今后在教学中还是要坚持学习了新的定理之后,要带着学生在课堂上书写证明过程。
切线长定理
教学目标
了解切线长的概念.
理解切线长定理,了解三角形的内切圆和三角形的内心的概念,熟练掌握它的应用.
复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理,然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念,最后应用它们解决一些实际问题.
重难点、关键
1.重点:切线长定理及其运用.
2.难点与关键:切线长定理的导出及其证明和运用切线长定理解决一些实际问题.
教学过程
一、复习引入
1.问题1、经过平面上一个已知点,作已知圆的切线会有怎样的情形?
2.问题2、经过圆外一点P,如何准确地作已知⊙O的切线?
二、探索新知
从上面的复习,我们可以知道,过⊙O上任一点A都可以作一条切线,并且只有一条,根据下面提出的问题操作思考并解决这个问题.
问题:在你手中的纸上画出⊙O,并画出过A点的唯一切线PA,连结PO,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性,说明圆中的PA与PB,∠APO与∠BPO有什么关系?
学生分组讨论,老师抽取3~4位同学回答这个问题.
我们把PA或PB的长,即经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
注意切线与切线长的区别
从上面的操作几何我们可以得到:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
下面,我们给予逻辑证明.
例1.如图,已知PA、PB是⊙O的两条切线.
求证:PA=PB,∠OPA=∠OPB.
因此,我们得到切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
小结:切线常用的6条性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。
6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
例1、PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。(幻灯片8)
(1)写出图中所有的垂直关系
(2)写出图中与∠OAC相等的角
(3)写出图中所有的全等三角形
(4)写出图中所有的等腰三角形
(5)若PA=4、PD=2,求半径OA
及时归纳:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
例2.如图所示PA、PB分别切圆O于A、B,并与圆O的切线分别相交于C、D,已知
PA=7cm,
(1)求△PCD的周长.
(2) 如果∠P=46°,求∠COD的度数(幻灯片10)
选做题:如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.(幻灯片11)
内切圆 内心
教学内容 1、三角形的内切圆及三角形内心的概念.
2、定理及概念的运用。
教学目标
复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理,然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念,最后应用它们解决一些实际问题.
教学过程:
一、复习引入:如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
二、探索新知:
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?(幻灯片2)
例1 、作圆,使它和已知三角形的各边都相切
已知: △ABC(如图)
求作:和△ABC的各边都相切的圆
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
问题4:在这块三角形材料上还能裁下更大的圆吗
三角形内切圆的圆心叫三角形的内心
三角形内心的性质:
例2、如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长。(幻灯片5)
(说明:此题为书上的例题,要让学生上黑板板书)
练习:1 如图,在△ABC中,点O是内心,(1)若∠ABC=50°∠ACB=70°,求∠BOC的度数。(幻灯片6)
2、已知△ABC的三边BC,AB,AC分别为a,b,c,I为内心,内切圆半径为r。求△ABC的面积。(幻灯片7)
归纳:三角形的内切圆与外接圆的异同比较(以表格的形式进行比较)
四、布置作业:P102 第6、7题;P103第14题。
A
O
.
O
A
l
C
O
A
B
P
O
C
E
D
。
P
A
O
反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
C
¤ O
P
B
D
A
E
· O
A
B
C
D
E
F
A
B
C
O
A
B
C
D
E
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
24.2.2直线与圆有关的位置关系
第1课时
教学目标
(1)了解直线和圆的位置关系的有关概念.
(2)理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:
直线L和⊙O相交d
(3)理解切线的判定定理:理解切线的性质定理并熟练掌握以上内容解决一些实际问题.
复习点和圆的位置关系,引入直线和圆的位置关系,以直线和圆的位置关系中的d=r直线和圆相切,讲授切线的判定定理和性质定理.
重难点、关键
1.重点:切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目.
2.难点与关键:由上节课点和圆的位置关系迁移并运动直线导出直线和圆的位置关系的三个对应等价.
教学过程
一、复习引入
(老师口答,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
二、探索新知
活动1:P93页思考:把海平面看作一条直线,太阳看作一个圆,由此你能得出直线与圆的位置关系吗?
由此你能归纳出直线和圆有几种位置关系吗?
( http: / / )
如图(a),直线L和圆有两个公共点,这时我们就说这条直线和圆( ),这条直线叫做圆的( ).
如图(b),直线和圆有一个公共点,这时我们说这条直线和圆( ),这条直线叫做圆的( ),这个点叫做( ).
如图(c),直线和圆没有公共点,这时我们说这条直线和圆( ).
活动2:判断正误:
1、 直线与圆最多有两个公共点 。…………………( )
2、 若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
3、 若A、B是⊙O外两点, 则直线AB与⊙O相离。… … … … …( )
4、 若C为⊙O内一点,则过点C的直线与⊙O相交。( )
活动3:思考:如何判断直线与圆的位置关系?
老师点评直线L和⊙O相交d
直线与圆的位置关系 相交 相切 相离
图 形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
活动4、练习1
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
3、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是____。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是 ___ _。
练习2
1、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为( )
A、d≤4 B、d<4 C、d≥4 D、d=4
2、设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是……………………………………………( )
A、相交 B、相切 C、相离 D、相切或相交
切线的判定
一、复习引入:直线与圆的三中位置关系中,最重要的是直线与圆相切,本节课重点研究这一种位置关系。
在证明“直线与圆相切 d=r”,其实证明了“垂直于切线的直径必过切点”,反之“经过切点且垂直于切线的直线必过圆心”也同样成立。(板书以上两条切线的性质)
探讨:过圆心且过切点的直线,是否垂直于切线呢?
二、探索新知:
活动1、已知直线l 是⊙O的切线,切点为A,连接0A,你发现了什么?
(幻灯片3、幻灯片4)结论:圆的切线垂直于过切点的半径。
综合以上三条切线的性质,可总结为:一条直线若满足①过圆心,②过切点,③垂直于切线这三条中的任意两条,就必然满足第三条。(板书)
活动2、画⊙O及半径OA,画一条直线l过半径OA的外端点,且垂直于OA。你发现直线l与⊙O有怎样的位置关系?为什么?
(幻灯片5)
因为d=r直线L和⊙O相切,这里的d是圆心O到直线L的距离,即垂直,并由d=r就可得到L经过半径r的外端,即半径OA的A点,因此,很明显的,我们可以得到切线的判定定理:(幻灯片6)
经过半径的外端并且垂直于这条半径的直线是圆的切线.(板书)
判断下图直线L是否是⊙O的切线?并说明为什么。(幻灯片7)
例1(P95例1)直线AB经过⊙O上的点C,并且OA=OB,CA=CB,
求证:直线AB是⊙O的切线.(幻灯片8)略
(学生分组讨论):根据上面的判定定理,如果你要证明一条直线是⊙O的切线,你应该如何证明?
(老师点评):应分为两步:(1)说明这个点是圆上的点,(2)过这点的半径垂直于直线.
练习:1.已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC, ∠A=30.求证:直线AB是⊙O的切线. (幻灯片9)
小结:辅助线:有点连圆心,证垂直
2.如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,判断⊙D与OA的位置关系, 并证明你的结论。(幻灯片10)
小结:辅助线:无点做垂线,证相等
例2、小红家的锅盖坏了,为了配一个锅盖,需要测量锅盖的直径(锅边所形成的圆的直径),而小红家只有一把长20cm 的直尺,根本不够长,怎么办呢 小红想了想,采取以下方法:首先把锅平放到墙根,锅边刚好靠到两墙,用直尺紧贴墙面量得MA的长,即可求出墙的直径,请你利用下图,说明她这样做的道理.
(幻灯片11)
练习:(幻灯片12、幻灯片13)
三、归纳小结:1、切线的性质定理;2、切线的三条判定定理;3、常见辅助线。
四、布置作业:P101习题24.2复习巩固4、5;
五、课后反思:本节课内容较多,由于安排得当,课堂完成情况较好;但是从作业中反映出的问题看,仍然存在着书写证明过程不规范、不严谨的问题。今后在教学中还是要坚持学习了新的定理之后,要带着学生在课堂上书写证明过程。
切线长定理
教学目标
了解切线长的概念.
理解切线长定理,了解三角形的内切圆和三角形的内心的概念,熟练掌握它的应用.
复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理,然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念,最后应用它们解决一些实际问题.
重难点、关键
1.重点:切线长定理及其运用.
2.难点与关键:切线长定理的导出及其证明和运用切线长定理解决一些实际问题.
教学过程
一、复习引入
1.问题1、经过平面上一个已知点,作已知圆的切线会有怎样的情形?
2.问题2、经过圆外一点P,如何准确地作已知⊙O的切线?
二、探索新知
从上面的复习,我们可以知道,过⊙O上任一点A都可以作一条切线,并且只有一条,根据下面提出的问题操作思考并解决这个问题.
问题:在你手中的纸上画出⊙O,并画出过A点的唯一切线PA,连结PO,沿着直线PO将纸对折,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的切线吗?利用图形的轴对称性,说明圆中的PA与PB,∠APO与∠BPO有什么关系?
学生分组讨论,老师抽取3~4位同学回答这个问题.
我们把PA或PB的长,即经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.
注意切线与切线长的区别
从上面的操作几何我们可以得到:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
下面,我们给予逻辑证明.
例1.如图,已知PA、PB是⊙O的两条切线.
求证:PA=PB,∠OPA=∠OPB.
因此,我们得到切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
小结:切线常用的6条性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心。
6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
例1、PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。(幻灯片8)
(1)写出图中所有的垂直关系
(2)写出图中与∠OAC相等的角
(3)写出图中所有的全等三角形
(4)写出图中所有的等腰三角形
(5)若PA=4、PD=2,求半径OA
及时归纳:在解决有关圆的切线长问题时,往往需要我们构建基本图形。
(1)分别连结圆心和切点
(2)连结两切点
(3)连结圆心和圆外一点
例2.如图所示PA、PB分别切圆O于A、B,并与圆O的切线分别相交于C、D,已知
PA=7cm,
(1)求△PCD的周长.
(2) 如果∠P=46°,求∠COD的度数(幻灯片10)
选做题:如图,AB是⊙O的直径,AD、DC、BC是切线,点A、E、B为切点,若BC=9,AD=4,求OE的长.(幻灯片11)
内切圆 内心
教学内容 1、三角形的内切圆及三角形内心的概念.
2、定理及概念的运用。
教学目标
复习圆与直线的位置关系和切线的判定定理、性质定理知识迁移到切长线的概念和切线长定理,然后根据所学三角形角平分线的性质给出三角形的内切圆和三角形的内心概念,最后应用它们解决一些实际问题.
教学过程:
一、复习引入:如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?
二、探索新知:
如图是一块三角形木料,木工师傅要从中裁下一块圆形用料,怎样才能使裁下的圆的面积尽可能大呢?(幻灯片2)
例1 、作圆,使它和已知三角形的各边都相切
已知: △ABC(如图)
求作:和△ABC的各边都相切的圆
问题1:作圆的关键是什么?
问题2:怎样确定圆心的位置?
问题3:圆心的位置确定后怎样确定圆的半径?
问题4:在这块三角形材料上还能裁下更大的圆吗
三角形内切圆的圆心叫三角形的内心
三角形内心的性质:
例2、如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=9cm,BC=14cm,CA=13cm,求AF,BD,CE的长。(幻灯片5)
(说明:此题为书上的例题,要让学生上黑板板书)
练习:1 如图,在△ABC中,点O是内心,(1)若∠ABC=50°∠ACB=70°,求∠BOC的度数。(幻灯片6)
2、已知△ABC的三边BC,AB,AC分别为a,b,c,I为内心,内切圆半径为r。求△ABC的面积。(幻灯片7)
归纳:三角形的内切圆与外接圆的异同比较(以表格的形式进行比较)
四、布置作业:P102 第6、7题;P103第14题。
A
O
.
O
A
l
C
O
A
B
P
O
C
E
D
。
P
A
O
反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。
C
¤ O
P
B
D
A
E
· O
A
B
C
D
E
F
A
B
C
O
A
B
C
D
E
F
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
