苏教版数学选修2导数的极值
图片预览



文档简介
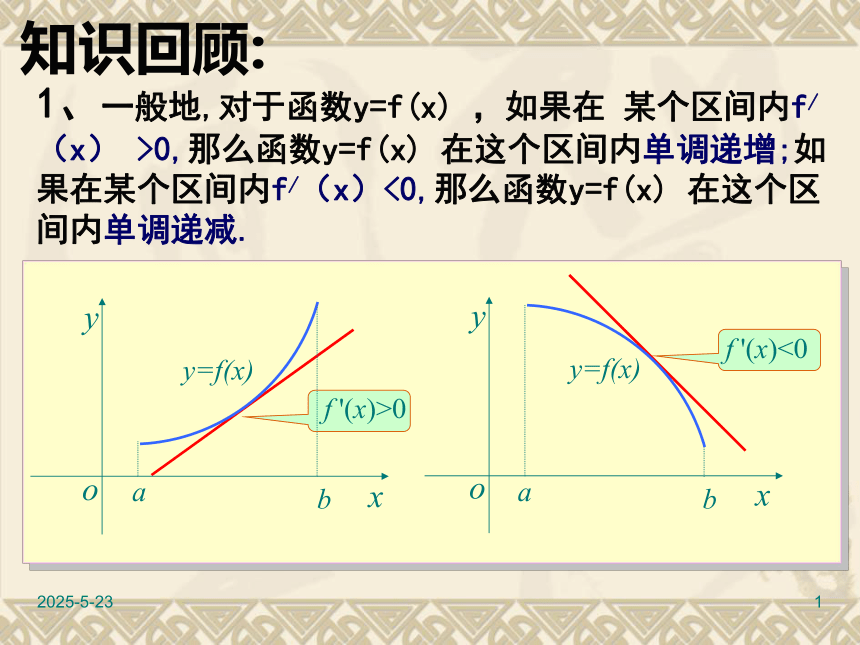
课件14张PPT。2019/3/101f '(x)>0f '(x)<01、一般地,对于函数y=f(x) ,如果在 某个区间内f/(x) >0,那么函数y=f(x) 在这个区间内单调递增;如果在某个区间内f/(x)<0,那么函数y=f(x) 在这个区间内单调递减.知识回顾:2019/3/1022.用导数求函数单调区间的一般步骤:①求函数的定义域; ②求函数的导数 f/(x) ; ③解不等式 f/(x)>0 得f(x)的单调递增区间;
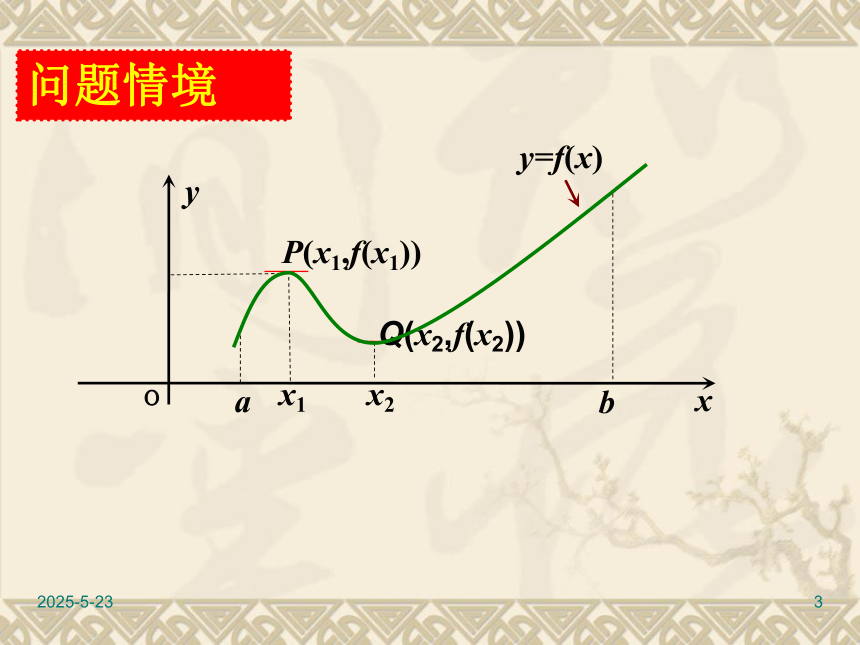
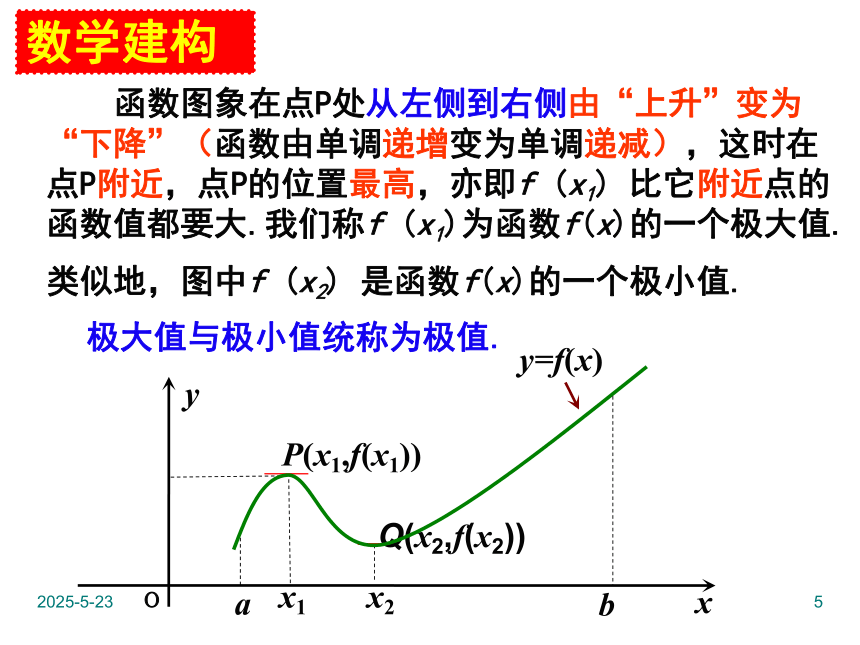
解不等式 f/(x)<0 得f(x)的单调递减区间.2019/3/103问题情境2019/3/104极大值与极小值2019/3/105数学建构 函数图象在点P处从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),这时在点P附近,点P的位置最高,亦即f (x1) 比它附近点的函数值都要大.我们称f (x1)为函数f(x)的一个极大值.极大值与极小值统称为极值.类似地,图中f (x2) 是函数f(x)的一个极小值.2019/3/106数学应用例1:利用图象判断下列几个函数是否有极值.
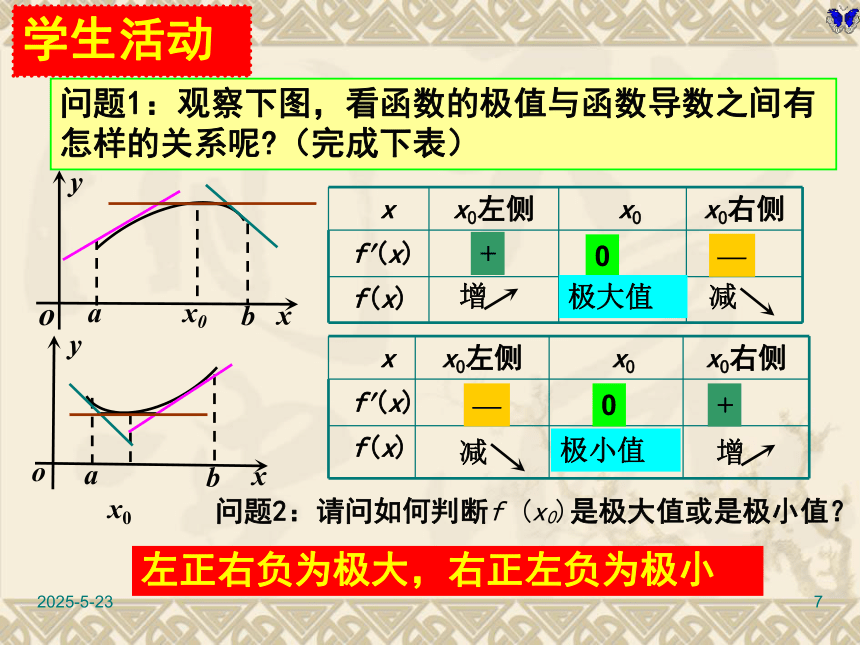
(1)(3)(2)2019/3/107问题1:观察下图,看函数的极值与函数导数之间有怎样的关系呢?(完成下表)0—极大值0极小值+问题2:请问如何判断f (x0)是极大值或是极小值?左正右负为极大,右正左负为极小—+学生活动2019/3/108数学应用例3:求函数 的极值.例2:求函数 的极值.2019/3/109 函数 的定义域为R,导函数 的图象如图所示,则函数 的图象上的极值点有 个.试一试2019/3/10103、求函数 的极值.学生练习1、利用导数知识,求函数
的极值.2、求函数 的极值.2019/3/1011问题3:由以上练习,请你说说 求函数的极值的步骤:① 确定函数的定义域;④ 根据 在 左右两侧的符号,确定极值。
(通过列表法)② 求导数 ;
学生活动2019/3/1012 函数 是否有极值?如果有,请求出;如果没有,请说明理由.思考2019/3/1013回顾小结请同学们想一想,本节课我们主要学习了哪些知识?2019/3/1014课外作业 见学案
解不等式 f/(x)<0 得f(x)的单调递减区间.2019/3/103问题情境2019/3/104极大值与极小值2019/3/105数学建构 函数图象在点P处从左侧到右侧由“上升”变为“下降”(函数由单调递增变为单调递减),这时在点P附近,点P的位置最高,亦即f (x1) 比它附近点的函数值都要大.我们称f (x1)为函数f(x)的一个极大值.极大值与极小值统称为极值.类似地,图中f (x2) 是函数f(x)的一个极小值.2019/3/106数学应用例1:利用图象判断下列几个函数是否有极值.
(1)(3)(2)2019/3/107问题1:观察下图,看函数的极值与函数导数之间有怎样的关系呢?(完成下表)0—极大值0极小值+问题2:请问如何判断f (x0)是极大值或是极小值?左正右负为极大,右正左负为极小—+学生活动2019/3/108数学应用例3:求函数 的极值.例2:求函数 的极值.2019/3/109 函数 的定义域为R,导函数 的图象如图所示,则函数 的图象上的极值点有 个.试一试2019/3/10103、求函数 的极值.学生练习1、利用导数知识,求函数
的极值.2、求函数 的极值.2019/3/1011问题3:由以上练习,请你说说 求函数的极值的步骤:① 确定函数的定义域;④ 根据 在 左右两侧的符号,确定极值。
(通过列表法)② 求导数 ;
学生活动2019/3/1012 函数 是否有极值?如果有,请求出;如果没有,请说明理由.思考2019/3/1013回顾小结请同学们想一想,本节课我们主要学习了哪些知识?2019/3/1014课外作业 见学案
