幂函数的概念
图片预览


文档简介
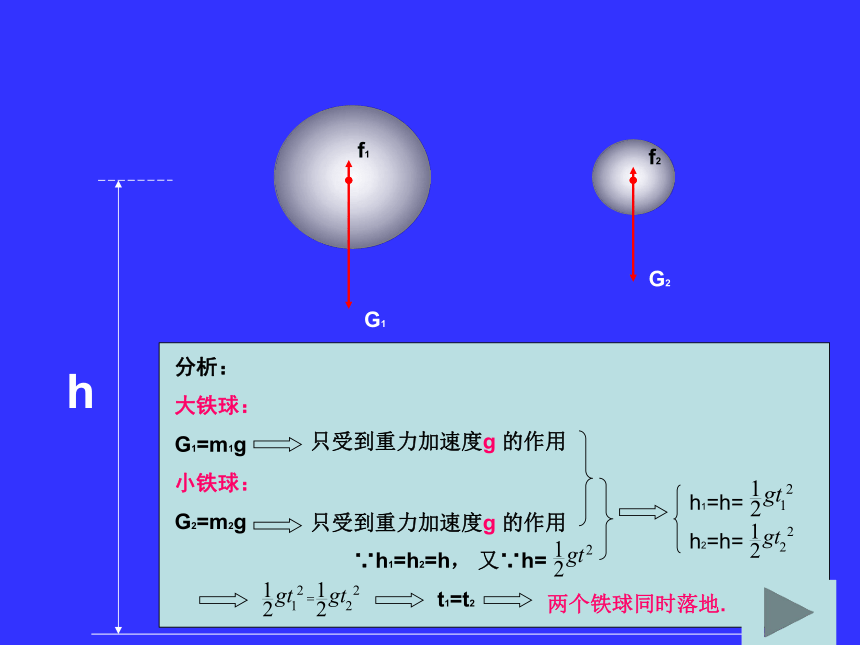
课件14张PPT。两个铁球同时落地hV0=0V0=0vhG1G2f1f2分析:
大铁球:
G1=m1g
小铁球:
G2=m2g
∵h1=h2=h, 又∵h=
t1=t2
h1=h=
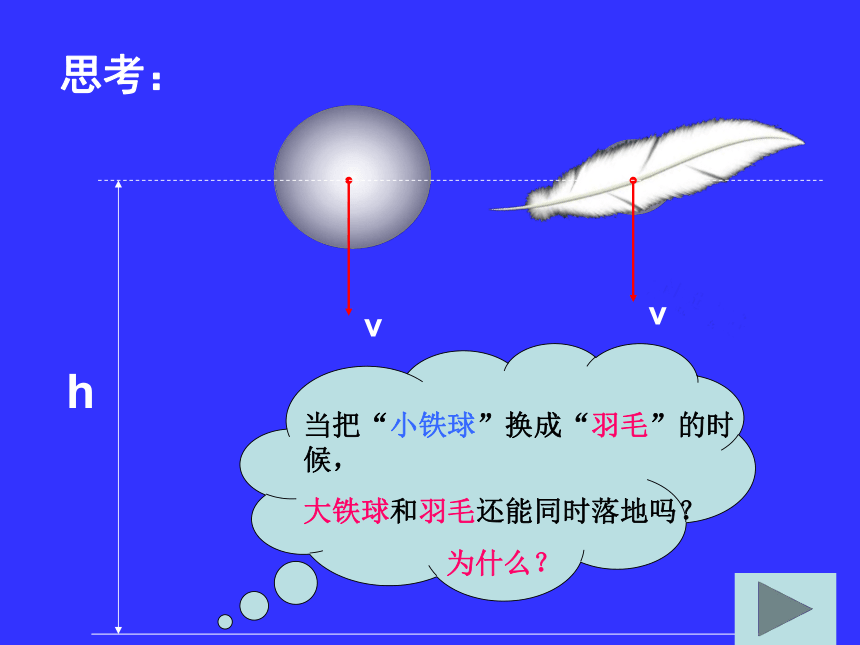
h2=h=只受到重力加速度g 的作用只受到重力加速度g 的作用两个铁球同时落地.hvv当把“小铁球”换成“羽毛”的时候,
大铁球和羽毛还能同时落地吗?
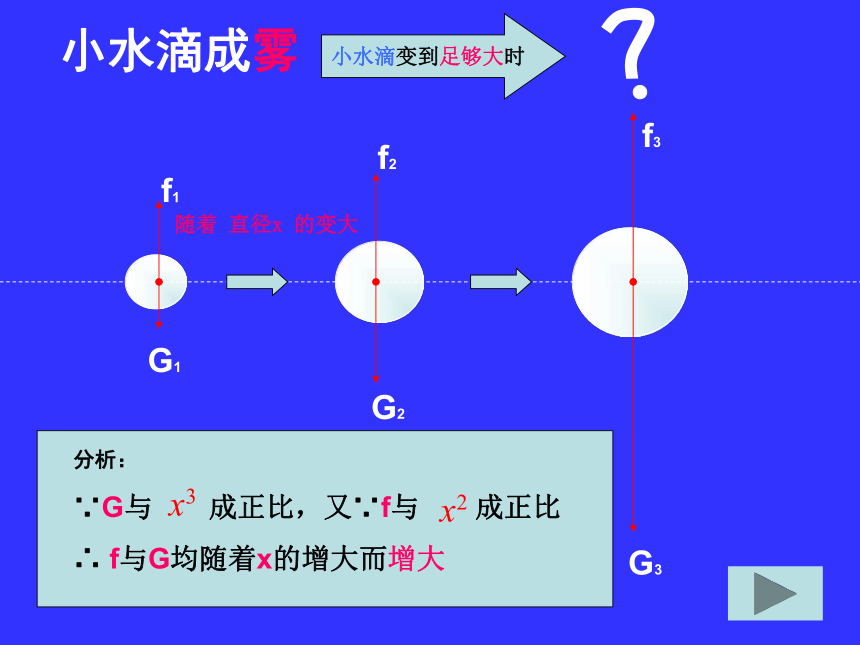
为什么?思考:小水滴成雾小水滴变到足够大时G1f1f3f2G3G2分析:
∵G与 成正比,又∵f与 成正比
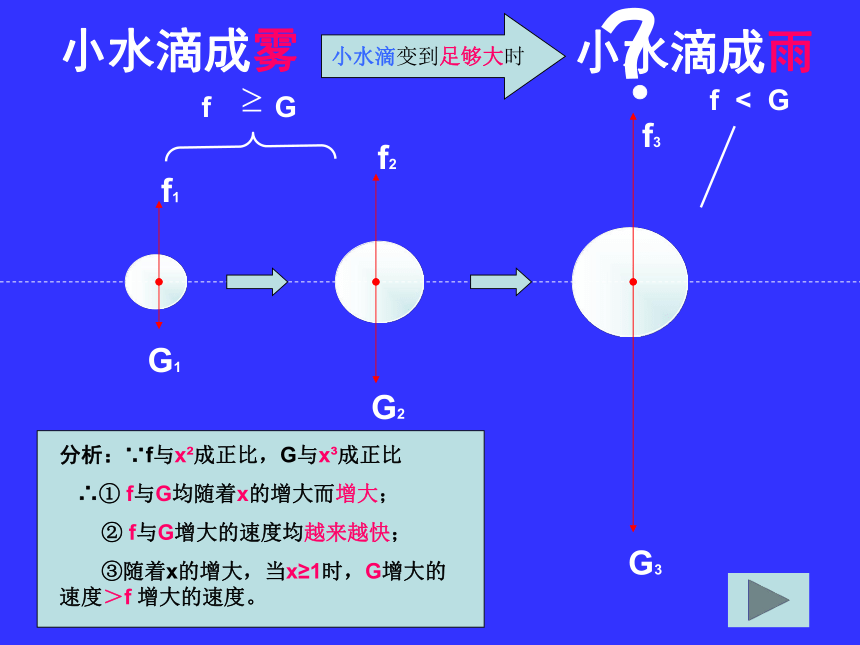
∴ f与G均随着x的增大而增大随着 直径x 的变大小水滴成雾小水滴变到足够大时小水滴成雨G1f1f3f2G3G2分析:∵f与x2成正比,G与x3成正比
∴① f与G均随着x的增大而增大;
② f与G增大的速度均越来越快;
③随着x的增大,当x≥1时,G增大的 速度>f 增大的速度。f Gf < G§2.3.1 幂函数的概念 正整数次的幂函数负整数次的幂函数分数次的幂函数(一)、正整数次的幂函数例:
①
②
③oyx11-1-1②当x≧0时,
三个函数均
单调递增。① 对称性
奇偶性(一)、正整数次的幂函数oyx11分析:当x≧0时:
① y=x 按同一个速度增长,y=x2 和 y=x3 均增长得越来越快。
②当0≦x<1时:
y=x 增长的速度> y=x2 增长的速度> y=x3 增长的速度。
当x 1时:
y=x 增长的速度< y=x2 增长的速度< y=x3 增长的速度。
∵f 与 x2成正比
∵G 与 x3成正比(二)、负整数次的幂函数例:
②
oyx11②当x>0时,
两个函数均
单调递减。 对称性
奇偶性(三)、分数次的幂函数例:
oyx②当x≧0时,
函数单调递增。①当开偶次方时,
非奇非偶函数11oyx11练习:①①②③④④⑤⑤⑥⑥奇函数:
即: , ,
偶函数:
即: ,
①、③、⑤④、⑥②
①
⑥④
⑤
③注意:
当x>0时,幂函数对数函数指数函数分析:当x>0时:
①当α>0时
②当α < 0时∵lnx递增
又∵ 递增递增∵lnx递增,∵ α < 0
又∵ 递增
αlnx递减递减作业课本p.111.
练习(3)、(4);
习题 1、2
大铁球:
G1=m1g
小铁球:
G2=m2g
∵h1=h2=h, 又∵h=
t1=t2
h1=h=
h2=h=只受到重力加速度g 的作用只受到重力加速度g 的作用两个铁球同时落地.hvv当把“小铁球”换成“羽毛”的时候,
大铁球和羽毛还能同时落地吗?
为什么?思考:小水滴成雾小水滴变到足够大时G1f1f3f2G3G2分析:
∵G与 成正比,又∵f与 成正比
∴ f与G均随着x的增大而增大随着 直径x 的变大小水滴成雾小水滴变到足够大时小水滴成雨G1f1f3f2G3G2分析:∵f与x2成正比,G与x3成正比
∴① f与G均随着x的增大而增大;
② f与G增大的速度均越来越快;
③随着x的增大,当x≥1时,G增大的 速度>f 增大的速度。f Gf < G§2.3.1 幂函数的概念 正整数次的幂函数负整数次的幂函数分数次的幂函数(一)、正整数次的幂函数例:
①
②
③oyx11-1-1②当x≧0时,
三个函数均
单调递增。① 对称性
奇偶性(一)、正整数次的幂函数oyx11分析:当x≧0时:
① y=x 按同一个速度增长,y=x2 和 y=x3 均增长得越来越快。
②当0≦x<1时:
y=x 增长的速度> y=x2 增长的速度> y=x3 增长的速度。
当x 1时:
y=x 增长的速度< y=x2 增长的速度< y=x3 增长的速度。
∵f 与 x2成正比
∵G 与 x3成正比(二)、负整数次的幂函数例:
②
oyx11②当x>0时,
两个函数均
单调递减。 对称性
奇偶性(三)、分数次的幂函数例:
oyx②当x≧0时,
函数单调递增。①当开偶次方时,
非奇非偶函数11oyx11练习:①①②③④④⑤⑤⑥⑥奇函数:
即: , ,
偶函数:
即: ,
①、③、⑤④、⑥②
①
⑥④
⑤
③注意:
当x>0时,幂函数对数函数指数函数分析:当x>0时:
①当α>0时
②当α < 0时∵lnx递增
又∵ 递增递增∵lnx递增,∵ α < 0
又∵ 递增
αlnx递减递减作业课本p.111.
练习(3)、(4);
习题 1、2
