数学(苏教版必修4):1.4.2《正弦函数、余弦函数的性质3》课件
文档属性
| 名称 | 数学(苏教版必修4):1.4.2《正弦函数、余弦函数的性质3》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 264.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-11-29 15:35:00 | ||
图片预览




文档简介
课件18张PPT。三角函数
1.4.2正弦函数余弦函数的性质
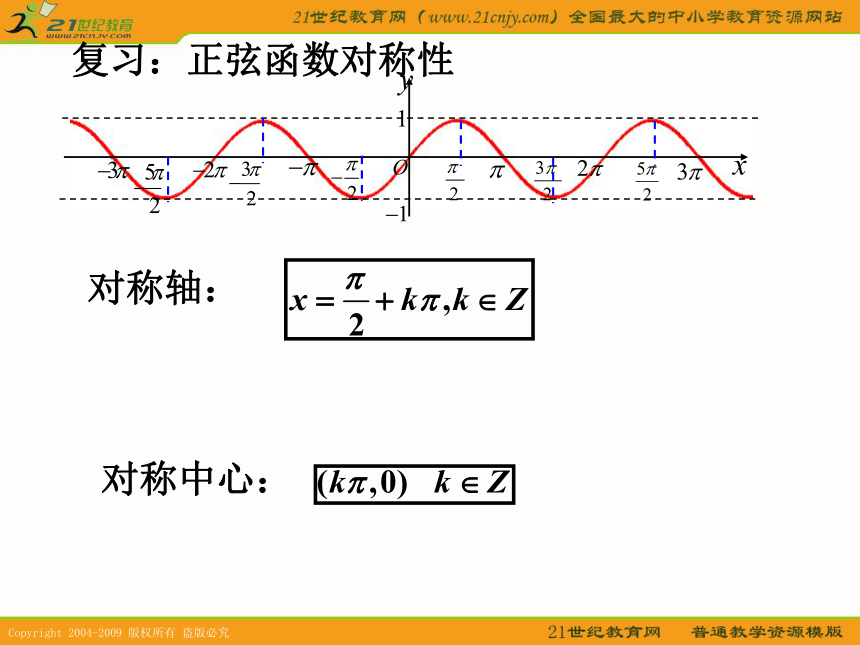
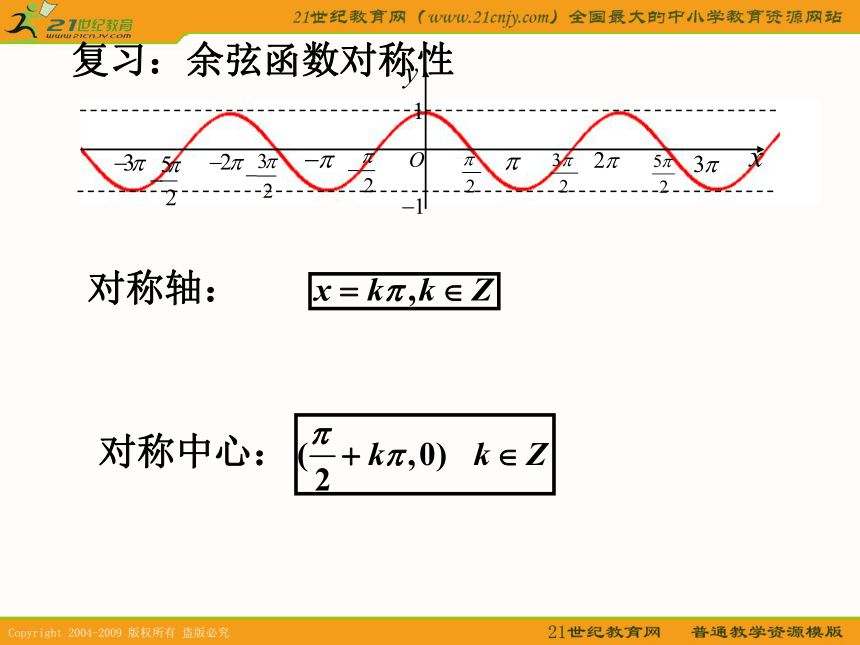
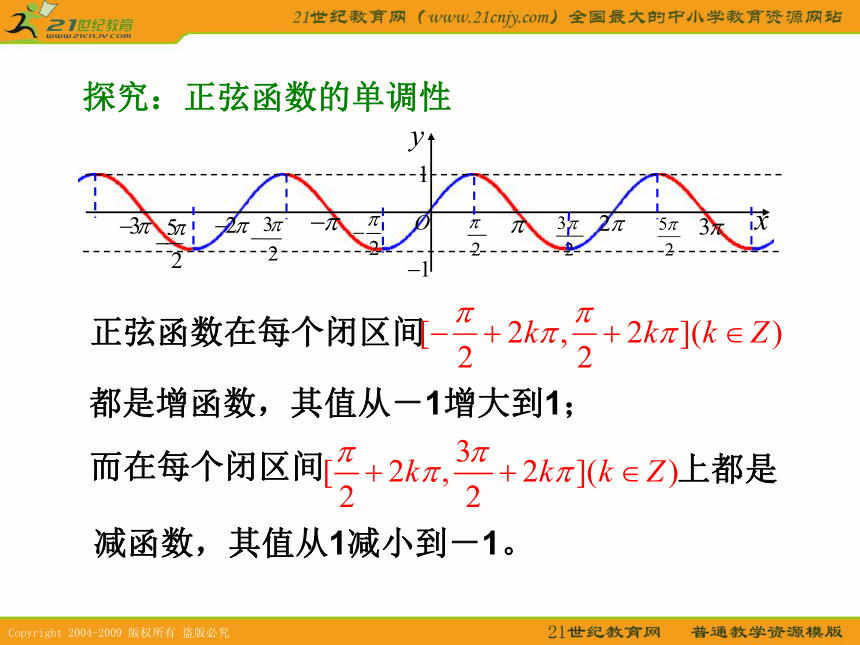
(三)定义域和值域正弦函数定义域:R值域:[-1,1]余弦函数定义域:R值域:[-1,1]1.周期性(复习)2.奇偶性为奇函数为偶函数复习:正弦函数对称性对称轴:对称中心:复习:余弦函数对称性对称轴:对称中心:探究:正弦函数的单调性正弦函数在每个闭区间都是增函数,其值从-1增大到1;减函数,其值从1减小到-1。探究:余弦函数的单调性由余弦函数的周期性知:其值从1减小到-1。其值从-1增大到1 ;探究:正弦函数的最大值和最小值最大值:当 时,有最大值最小值:当 时,有最小值探究:余弦函数的最大值和最小值最大值:当 时,有最大值最小值:当 时,有最小值分析:比较同名函数值的大小,往往可以利用函数的单调性,但需要考虑它是否在同一单调区间上,若是,即可判断,若不是,需化成同一单调区间后再作判断。例4:不求值,判断下列各式的符号。解:练习P46 练习5 (1)(2)练习P46 练习5 (3)(4)P45例5练习P46 练习6P45例5的深化小结1.比较大小:化到同一单调区间(结合图象)化未知为已知作业A. 小结
B. 求 的单调区间
P53 A4 (2)(3)
B. 求 的单调区间
P53 A4 (2)(3)
