2。2。2 椭圆的几何性质
图片预览



文档简介
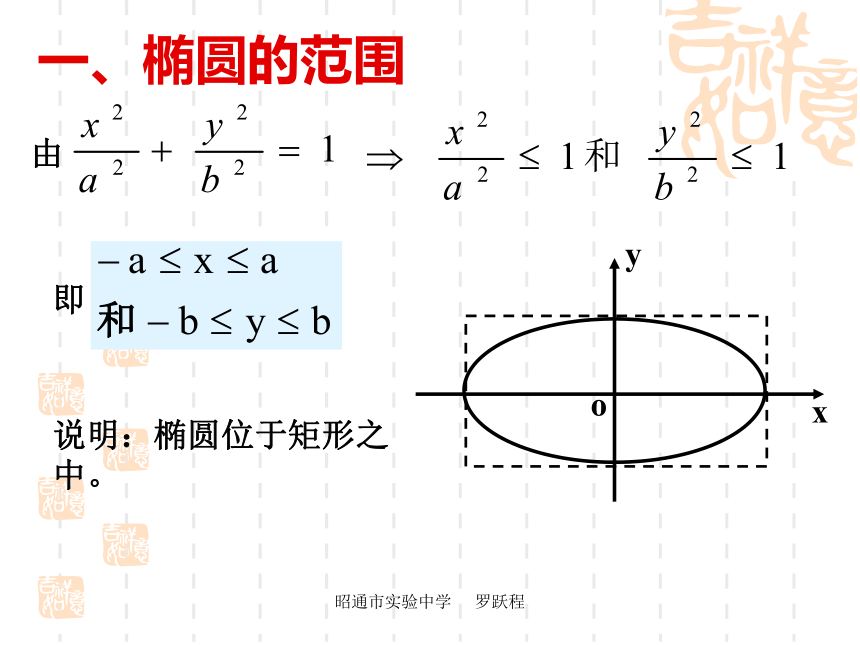
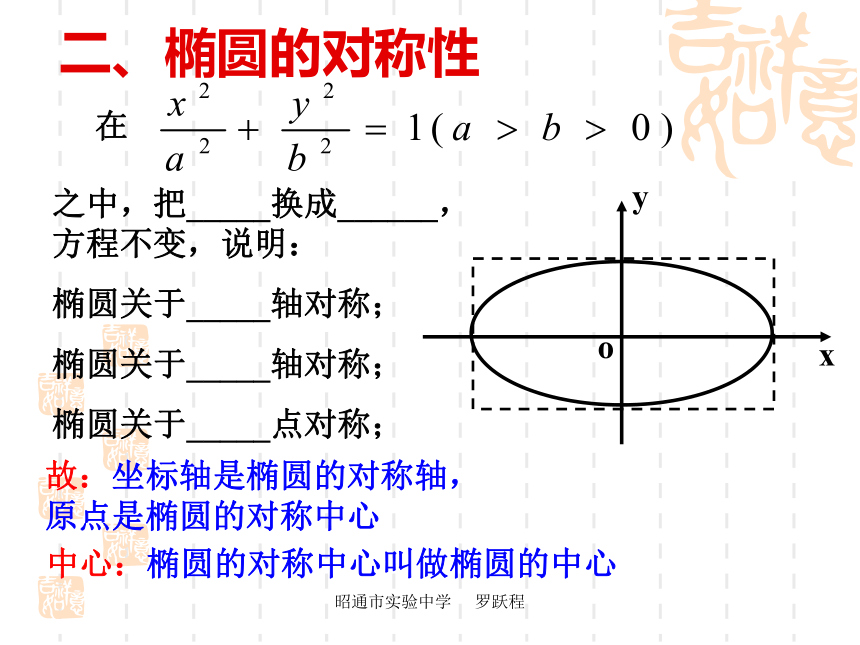
课件26张PPT。昭通市实验中学 罗跃程2.2.2《椭圆的几何性质》数学是思维的体操数学的美是在探究中发现的昭通市实验中学 罗跃程1、 圆的轨迹定义、标准方程、几何性质 2、平面解析几何研究的两个主要问题(1)根据已知条件,求出表示平面曲线的方程(2)通过方程,研究平面曲线的性质温故而知新昭通市实验中学 罗跃程一、椭圆的范围由说明:椭圆位于矩形之中。即昭通市实验中学 罗跃程二、椭圆的对称性之中,把_____换成______,方程不变,说明:
椭圆关于_____轴对称;
椭圆关于_____轴对称;
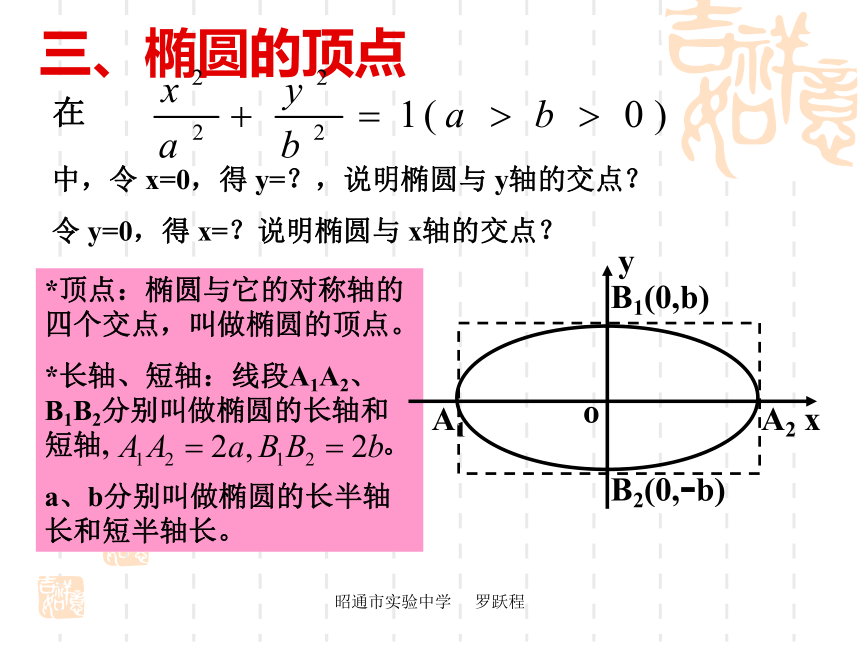
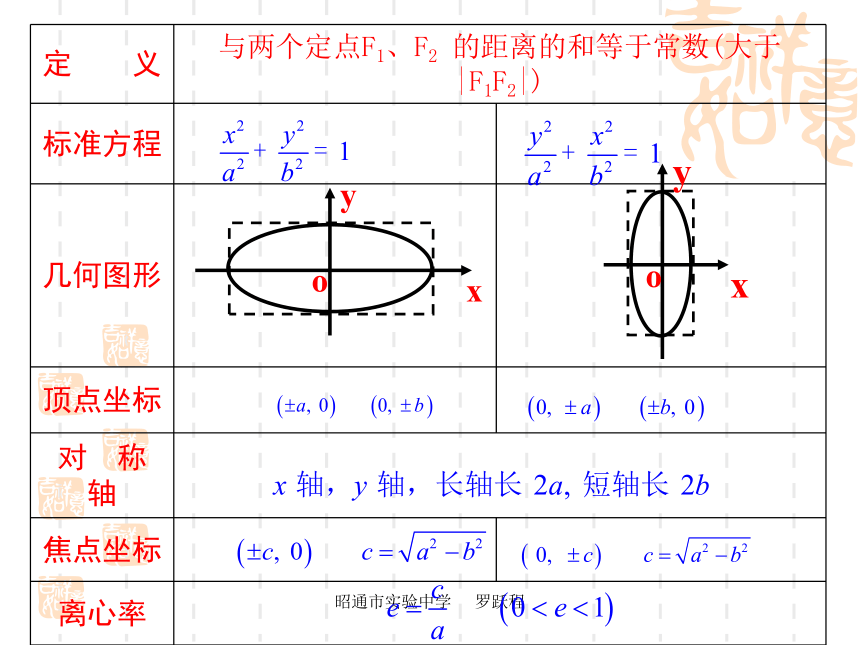
椭圆关于_____点对称;中心:椭圆的对称中心叫做椭圆的中心故:坐标轴是椭圆的对称轴, 原点是椭圆的对称中心昭通市实验中学 罗跃程三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴, 。
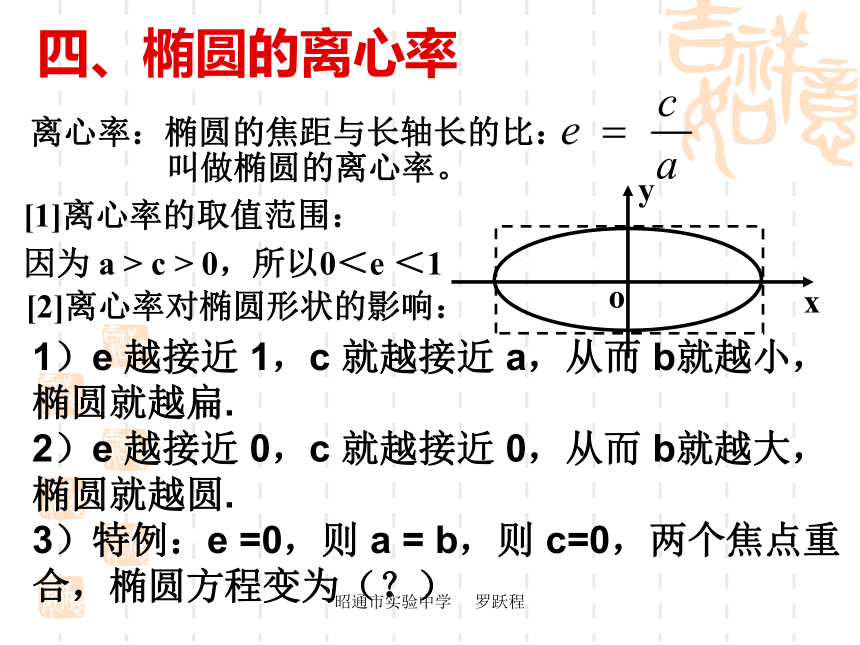
a、b分别叫做椭圆的长半轴长和短半轴长。昭通市实验中学 罗跃程四、椭圆的离心率[1]离心率的取值范围:
因为 a > c > 0,所以0<e <1[2]离心率对椭圆形状的影响:1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁.
2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆.
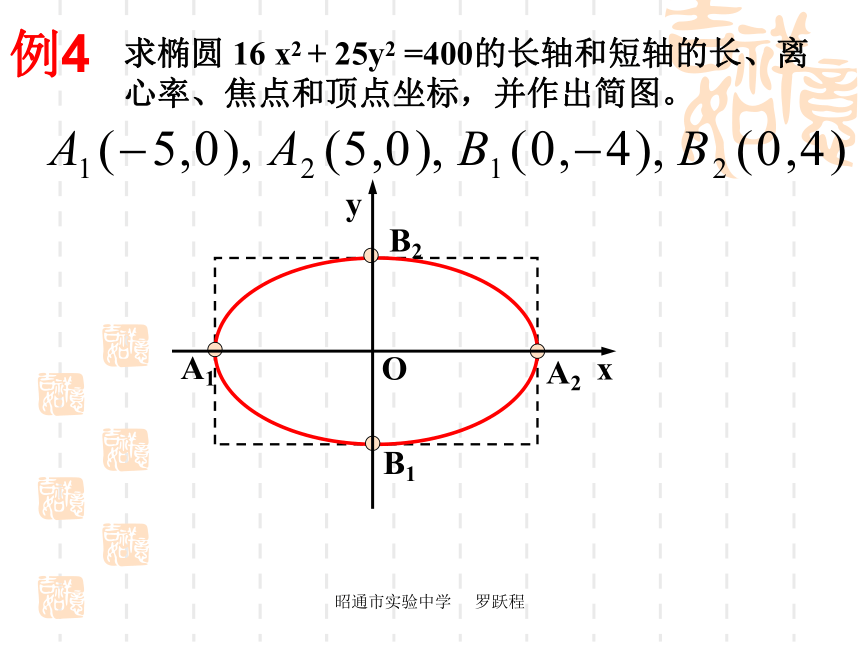
3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)昭通市实验中学 罗跃程昭通市实验中学 罗跃程例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并作出简图。解:把已知方程化成标准方程这里,因此,椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是昭通市实验中学 罗跃程例4 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并作出简图。昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程概念分析昭通市实验中学 罗跃程第二定义的“三定”:
定点是焦点;定直线是准线;定值是离心率的准线是y=的准线是x=昭通市实验中学 罗跃程1、求下列椭圆的准线方程:
①x2+4y2=4 ②2.已知P是椭圆 上的点,P到右准线的距离为8.5,则P到左焦点的距离为_________.昭通市实验中学 罗跃程练 习 (a>b>0)左焦点为F1,右焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ex0,|PF2|=a-ex0。其中|PF1|、 |PF2|叫焦半径. (a>b>0)下焦点为F1,上焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ey0,|PF2|=a-ey0。其中|PF1|、 |PF2|叫焦半径.说明:练习:已知椭圆 P为椭圆在第一象限内的点,它
与两焦点的连线互相垂直,求P点的坐标。昭通市实验中学 罗跃程练习1:求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 。昭通市实验中学 罗跃程练习2:已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。解析:由题可得:设椭圆方程为:又椭圆方程为:昭通市实验中学 罗跃程练习3:已知椭圆的中心在原点,一个顶点和一个焦点分
别是直线 x + 3y –6=0与两坐标轴的交点,求它的标
准方程。解:如右图所示,若A(6,0)为顶点,B(0, 2)为焦点,x所以椭圆的标准方程为 则b=6 , c=2, a2=b2+c2=40. 此时椭圆的标准方程为昭通市实验中学 罗跃程4、已知P点在椭圆 上,且P到椭圆左、右焦点的距离之比为1:4,求P到两准线的距离.5、求中心在原点、焦点在x轴上、其长轴端点与最近的焦点相距为1、与相近的一条准线距离为 的椭圆标准方程。昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程9:已知 是椭圆 的两个焦点,
P是椭圆上任一点。
(1)若 求 的面积。
(2)求 的最大值。昭通市实验中学 罗跃程[1] 椭圆标准方程所表示的椭圆的存在范围是什么?[2] 上述方程表示的椭圆有几个对称轴?几个对称中心?[3] 椭圆有几个顶点?顶点是谁与谁的交点?[4] 对称轴与长轴、短轴是什么关系?[5] 2a 和 2b是什么量?
a和 b是什么量?[6] 关于离心率讲了几点?回 顾
椭圆关于_____轴对称;
椭圆关于_____轴对称;
椭圆关于_____点对称;中心:椭圆的对称中心叫做椭圆的中心故:坐标轴是椭圆的对称轴, 原点是椭圆的对称中心昭通市实验中学 罗跃程三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点?
令 y=0,得 x=?说明椭圆与 x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴, 。
a、b分别叫做椭圆的长半轴长和短半轴长。昭通市实验中学 罗跃程四、椭圆的离心率[1]离心率的取值范围:
因为 a > c > 0,所以0<e <1[2]离心率对椭圆形状的影响:1)e 越接近 1,c 就越接近 a,从而 b就越小,椭圆就越扁.
2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆.
3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)昭通市实验中学 罗跃程昭通市实验中学 罗跃程例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并作出简图。解:把已知方程化成标准方程这里,因此,椭圆的长轴长和短轴长分别是离心率焦点坐标分别是四个顶点坐标是昭通市实验中学 罗跃程例4 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并作出简图。昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程概念分析昭通市实验中学 罗跃程第二定义的“三定”:
定点是焦点;定直线是准线;定值是离心率的准线是y=的准线是x=昭通市实验中学 罗跃程1、求下列椭圆的准线方程:
①x2+4y2=4 ②2.已知P是椭圆 上的点,P到右准线的距离为8.5,则P到左焦点的距离为_________.昭通市实验中学 罗跃程练 习 (a>b>0)左焦点为F1,右焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ex0,|PF2|=a-ex0。其中|PF1|、 |PF2|叫焦半径. (a>b>0)下焦点为F1,上焦点为F2,P0(x0,y0)为椭圆上一点,则|PF1|=a+ey0,|PF2|=a-ey0。其中|PF1|、 |PF2|叫焦半径.说明:练习:已知椭圆 P为椭圆在第一象限内的点,它
与两焦点的连线互相垂直,求P点的坐标。昭通市实验中学 罗跃程练习1:求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 。昭通市实验中学 罗跃程练习2:已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。解析:由题可得:设椭圆方程为:又椭圆方程为:昭通市实验中学 罗跃程练习3:已知椭圆的中心在原点,一个顶点和一个焦点分
别是直线 x + 3y –6=0与两坐标轴的交点,求它的标
准方程。解:如右图所示,若A(6,0)为顶点,B(0, 2)为焦点,x所以椭圆的标准方程为 则b=6 , c=2, a2=b2+c2=40. 此时椭圆的标准方程为昭通市实验中学 罗跃程4、已知P点在椭圆 上,且P到椭圆左、右焦点的距离之比为1:4,求P到两准线的距离.5、求中心在原点、焦点在x轴上、其长轴端点与最近的焦点相距为1、与相近的一条准线距离为 的椭圆标准方程。昭通市实验中学 罗跃程昭通市实验中学 罗跃程昭通市实验中学 罗跃程9:已知 是椭圆 的两个焦点,
P是椭圆上任一点。
(1)若 求 的面积。
(2)求 的最大值。昭通市实验中学 罗跃程[1] 椭圆标准方程所表示的椭圆的存在范围是什么?[2] 上述方程表示的椭圆有几个对称轴?几个对称中心?[3] 椭圆有几个顶点?顶点是谁与谁的交点?[4] 对称轴与长轴、短轴是什么关系?[5] 2a 和 2b是什么量?
a和 b是什么量?[6] 关于离心率讲了几点?回 顾
