勾股定理的复习
图片预览

文档简介
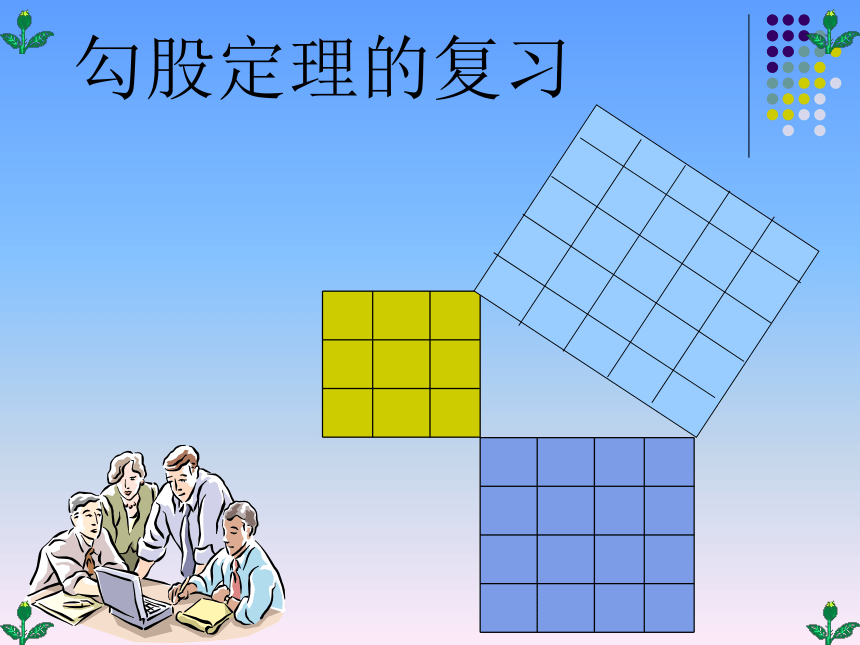
课件20张PPT。勾股定理的复习
思一思: 本章主要讲了哪几模块知识,各有何作用?勾股定理
逆定理
应用 直角三角形得到三边关系 由三边关系判断直角三角形 构造直角三角形,利用勾股
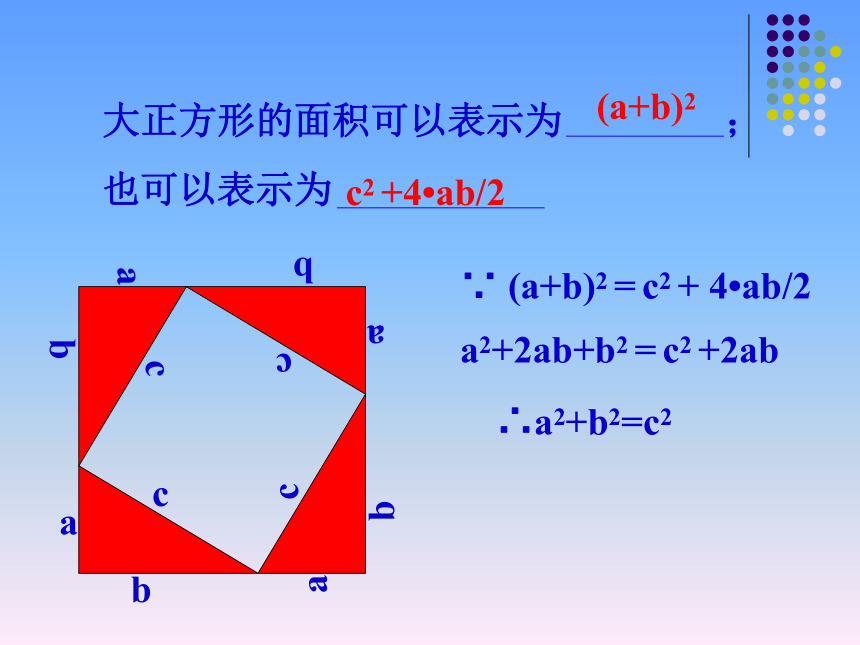
定理和逆定理 画一画: 勾股定理在生活中应用十分广泛,来源于生活。你能用 几种方法得到勾股定理 并证明 ∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
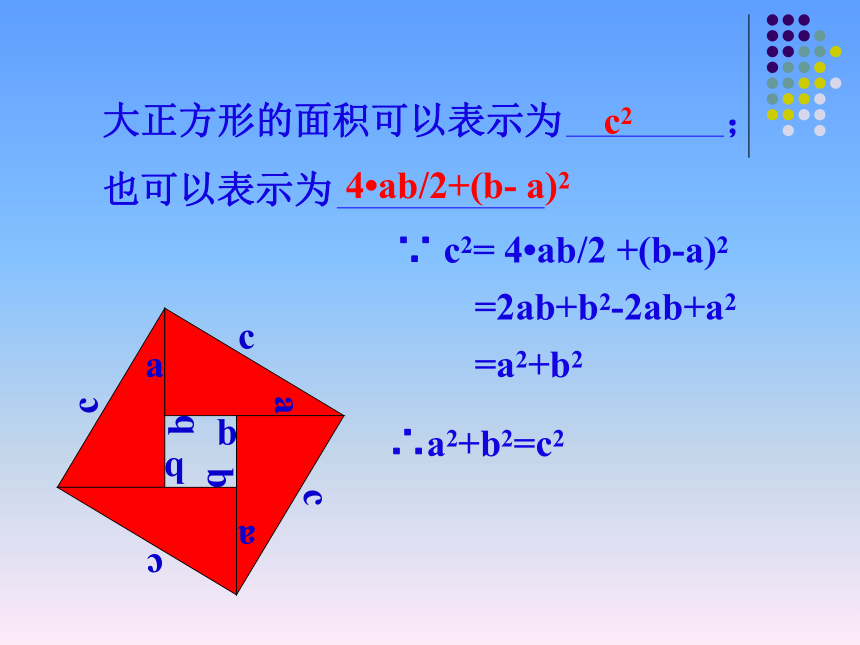
也可以表示为(a+b)2c2 +4?ab/2∵ c2= 4?ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24?ab/2+(b- a)2
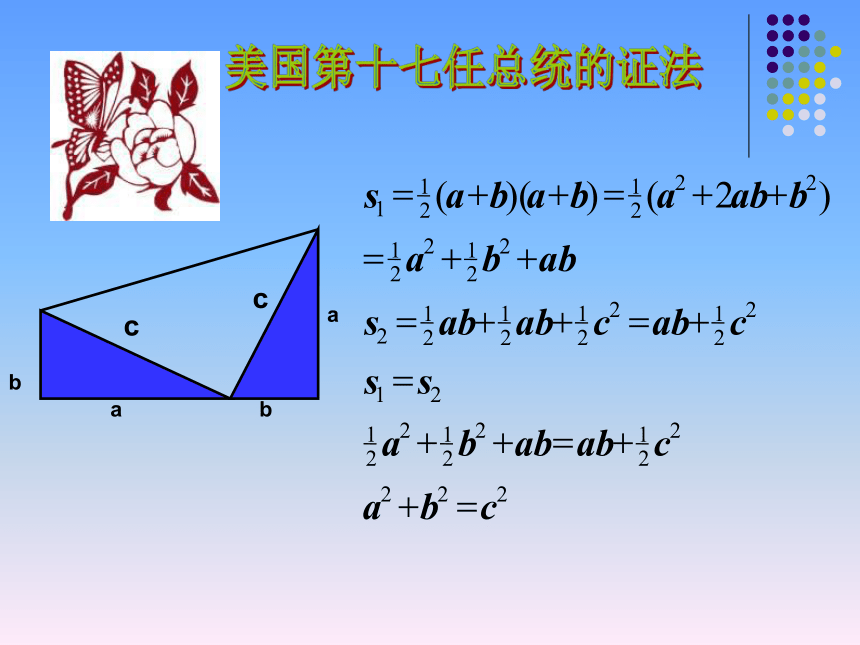
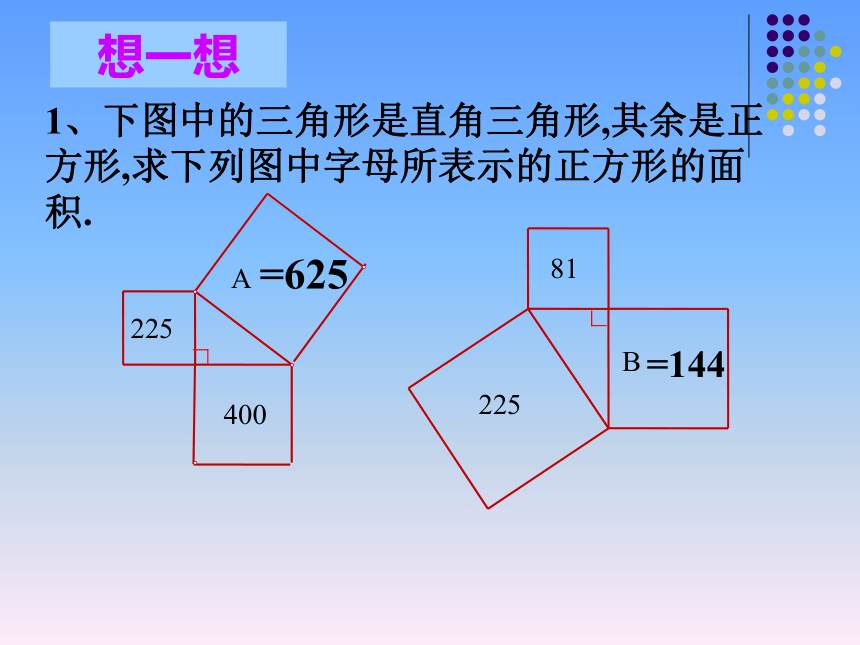
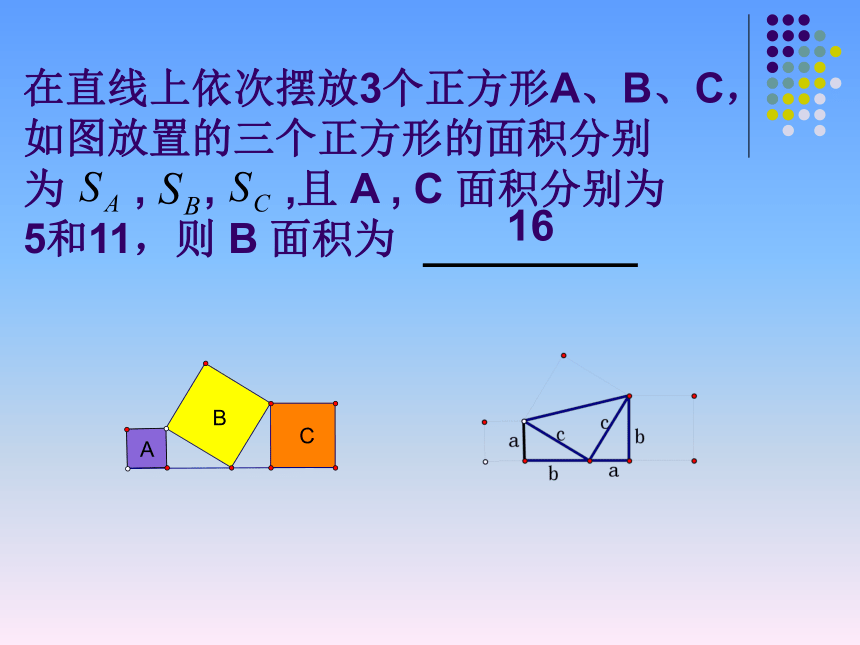
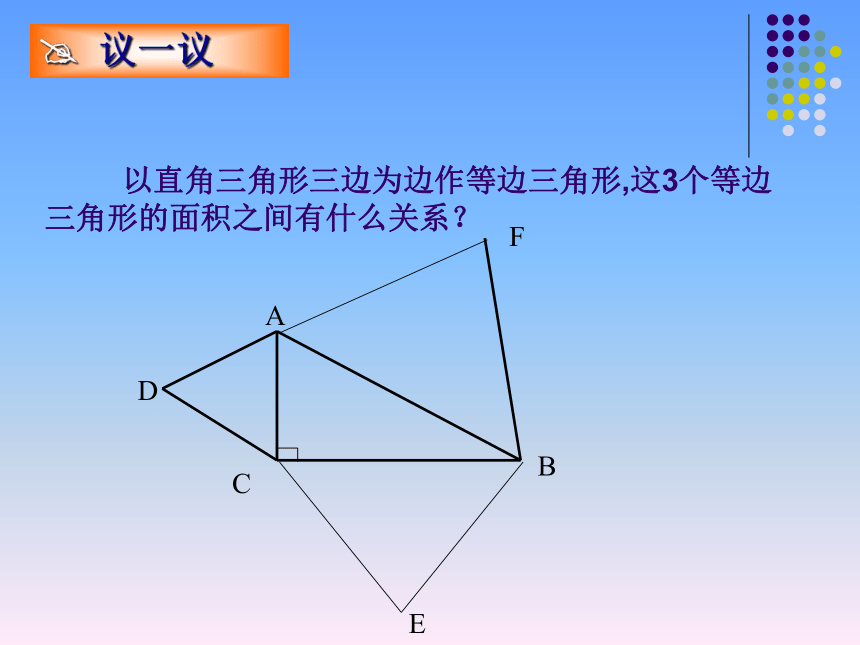
美国第十七任总统的证法1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想在直线上依次摆放3个正方形A、B、C, 如图放置的三个正方形的面积分别为 , , ,且 A , C 面积分别为 5和11,则 B 面积为 16 以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?? 议一议 神奇勾股数 学习了勾股定理这一章你能说出多少组勾股数? 3 , 4 , 5,
5,12, 13,
· · ·
· · ·
· · ·
6 ,8 ,10
8 , 15,17
· · ·
· · ·
· · ·如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:
(1) 从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为2 ;
(2) 画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且另两边的长度都是无理数.A分析 只需利用勾股定理看哪一个矩形的对角线满足要求.解 (1) 图1中AB长度为2 .(2) 图2中△ABC、△ABD就是所要画的等腰三角形.图1图2CB网格与勾股定理 .BDDA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的距离相等,试问这棵树有多高?DABC10米20米┏用勾股定理建立方程矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求线段EC的长。ABCDFE◆在上面的木箱中,如果在箱外的A处有一只昆虫.
⑴它要在箱壁上爬行到箱内的D处,至少要爬多远?⑵它要在箱壁上爬行到箱内的C处,至少要爬多远? ACBD怎样走最近问题:如图所示,有一个圆柱,它的高为12厘米,它的半径为3厘米,在圆柱底的A点有一只蚂蚁,它想吃到上面与A对应的B点 的食物,需要爬行的最短路程是多少?
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱
侧面画出几条路线,你 觉得哪条路最近?如图所示,将圆柱侧面剪开展成一个长方形,从A点到B点最短路线是什么?你画对了吗? (2)赠送给同学们十六个字:
题不在多,有心则灵!题海无边,回头是岸; 今日事 今日毕?我最大的收获是……??
课堂聚焦 再 见
思一思: 本章主要讲了哪几模块知识,各有何作用?勾股定理
逆定理
应用 直角三角形得到三边关系 由三边关系判断直角三角形 构造直角三角形,利用勾股
定理和逆定理 画一画: 勾股定理在生活中应用十分广泛,来源于生活。你能用 几种方法得到勾股定理 并证明 ∵ (a+b)2 = c2 + 4?ab/2a2+2ab+b2 = c2 +2ab∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为(a+b)2c2 +4?ab/2∵ c2= 4?ab/2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ;
也可以表示为c24?ab/2+(b- a)2
美国第十七任总统的证法1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625=144想一想在直线上依次摆放3个正方形A、B、C, 如图放置的三个正方形的面积分别为 , , ,且 A , C 面积分别为 5和11,则 B 面积为 16 以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?? 议一议 神奇勾股数 学习了勾股定理这一章你能说出多少组勾股数? 3 , 4 , 5,
5,12, 13,
· · ·
· · ·
· · ·
6 ,8 ,10
8 , 15,17
· · ·
· · ·
· · ·如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在给定网格中按下列要求画出图形:
(1) 从点A出发画一条线段AB,使它的另一个端点B在格点(即小正方形的顶点)上,且长度为2 ;
(2) 画出所有的以(1)中的AB为边的等腰三角形,使另一个顶点在格点上,且另两边的长度都是无理数.A分析 只需利用勾股定理看哪一个矩形的对角线满足要求.解 (1) 图1中AB长度为2 .(2) 图2中△ABC、△ABD就是所要画的等腰三角形.图1图2CB网格与勾股定理 .BDDA3、蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE 在一棵树的10米高的D处有两只猴子,其中一只猴子爬下树走到离树20米的池塘A处,另一只爬到树顶后直接跃向池塘A处,如果两只猴子所经过的距离相等,试问这棵树有多高?DABC10米20米┏用勾股定理建立方程矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求线段EC的长。ABCDFE◆在上面的木箱中,如果在箱外的A处有一只昆虫.
⑴它要在箱壁上爬行到箱内的D处,至少要爬多远?⑵它要在箱壁上爬行到箱内的C处,至少要爬多远? ACBD怎样走最近问题:如图所示,有一个圆柱,它的高为12厘米,它的半径为3厘米,在圆柱底的A点有一只蚂蚁,它想吃到上面与A对应的B点 的食物,需要爬行的最短路程是多少?
(1)自己做 一个圆柱,尝试从A点到B点沿圆柱
侧面画出几条路线,你 觉得哪条路最近?如图所示,将圆柱侧面剪开展成一个长方形,从A点到B点最短路线是什么?你画对了吗? (2)赠送给同学们十六个字:
题不在多,有心则灵!题海无边,回头是岸; 今日事 今日毕?我最大的收获是……??
课堂聚焦 再 见
同课章节目录
