北师大八年级上探索勾股定理说课稿

课件30张PPT。探 索 勾 股 定 理说课程序一、教材分析
二、教法与学法的分析
三、教学程序设计
四、教学评价分析
一、教材分析(一)教材的地位与作用
这节课是九年制义务教育初级中学教材北师大版八年级第一章第1节《探索勾股定理》第一课时，勾股定理是反映自然界基本规律的一条重要结论，有着悠久的历史；也是几何中几个重要定理之一，揭示的是直角三角形中三边的数量关系。它在数学的发展中起过重要的作用，在现实世界中也有着广泛的作用。学生通过对勾股定理的学习，可以在原有的基础上对直角三角形有进一步的认识和理解。 （二）教学目标
1、经历用数格子的办法探索勾股定理的过程，进一步发展学生的合情推理意识，主动探究的习惯，进一步体会数学与现实生活的紧密联系。
2、探索并理解直角三角形的三边之间的数量关系，进一步发展学生的说理和简单的推理的意识及能力。
3、在探索勾股定理的过程中，让学生经历“观察—猜想—归纳—验证”的数学思想，并体会数形结合和特殊到一般的思想方法。
4、通过介绍勾股定理在中国古代的研究，激发学生热爱祖国，热爱祖国悠久文化的思想，激励学生发奋学习。
（三）教学重点、难点、关键
重点:了解勾股定理的由来，并能用它来解决一些简单的问题。定理的灵活应用是难点；学生如何顺利探索的本课的关键。 二、教法与学法分析 教法分析:
本课具有可操作性，可研究性，可用直观数据检验的特点，因此采用探究发现式的教学方法，安排了三个探究活动，通过方格纸为学生设计一个合适的学习铺垫，引发学生的数学猜想，通过观察、计算、多媒体辅助演示，使学习内容不是单纯由教师传授，而是在教师的引导下达到知识的顺利迁移和综合内化，使学生充分体会到探究学习的成就感。另外通过设置情境法，激发学生的学习与研究数学的兴趣和积极性。基本教学流程是：提出问题—实验操作—归纳验证—问题解决—课堂小结—布置作业六部分 。
学法分析：
在教师的组织引导下，采用自主探索、合作交流、动手实践的研讨式学习方式，让学生思考问题，获取知识，掌握方法，借此培养学生动手、动脑、动口的能力，使学生真正成为学习的主体。
三、教学程序（一）创设问题情境导入新课如果云梯的最大长度为25米，云梯低端离墙的距离为7米，若失火点在8层处（每层3米），那么消防队员能否达到这样的高度？请说明理由。
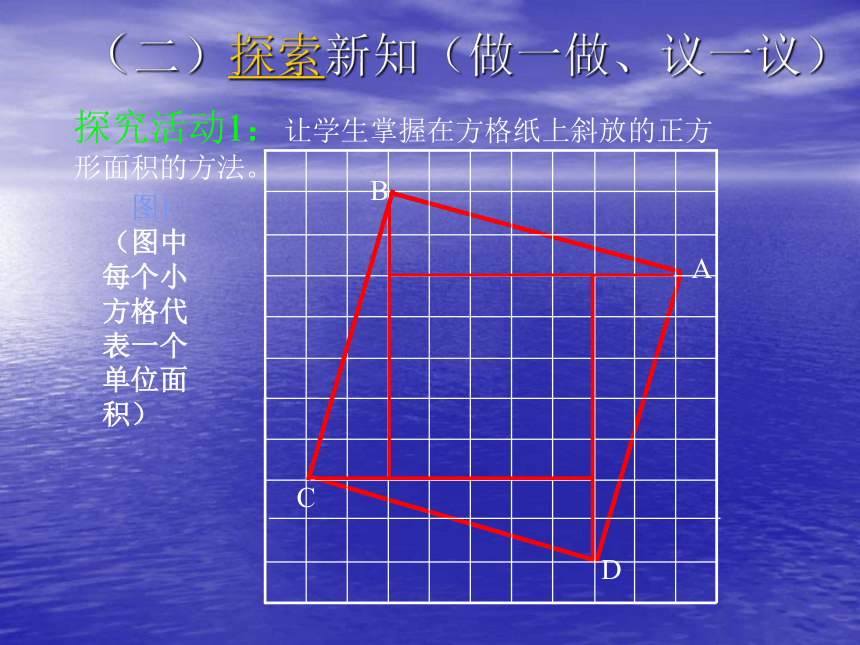
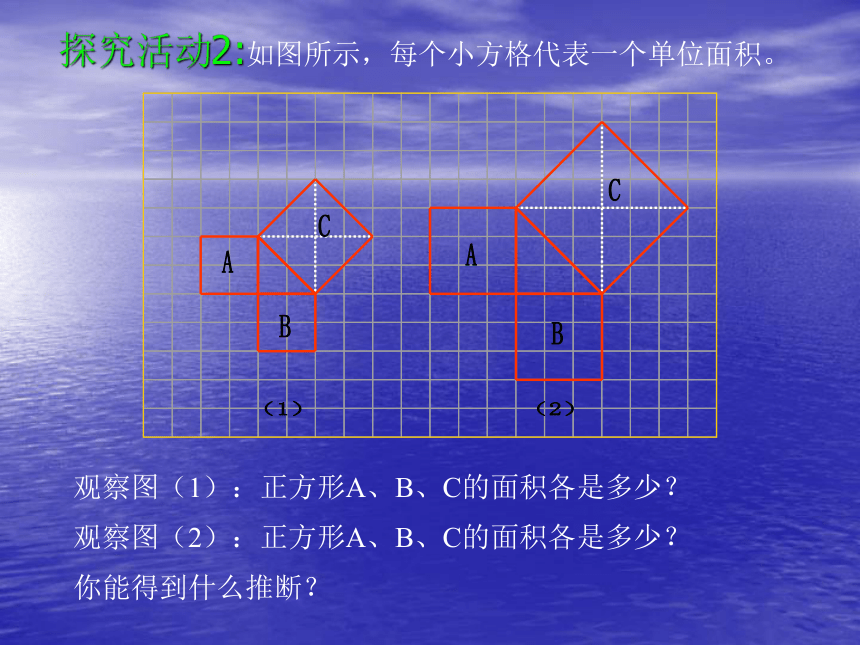
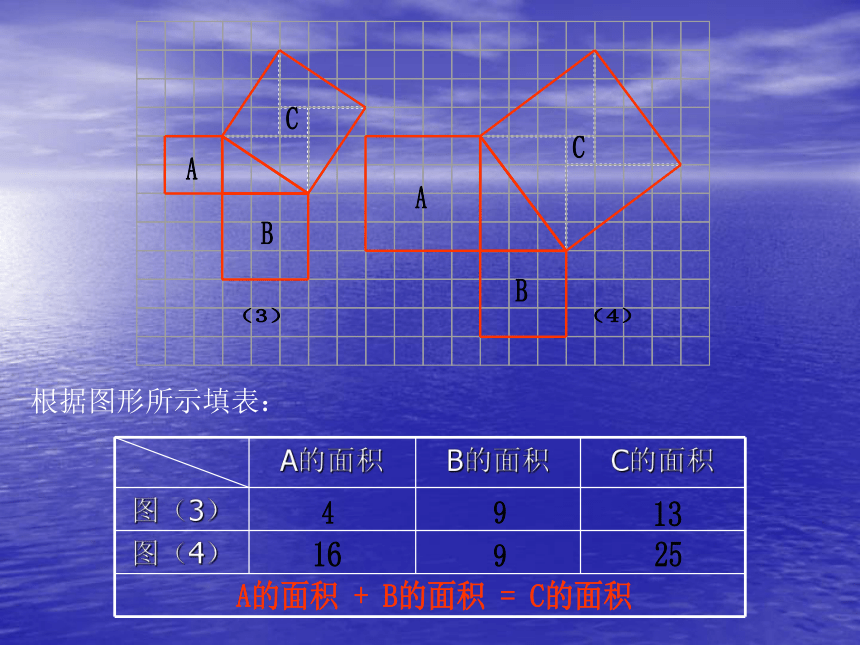
（二）探索新知（做一做、议一议）探究活动1：让学生掌握在方格纸上斜放的正方形面积的方法。 图1（图中每个小方格代表一个单位面积）探究活动2:如图所示，每个小方格代表一个单位面积。观察图（1）：正方形A、B、C的面积各是多少？观察图（2）：正方形A、B、C的面积各是多少？你能得到什么推断？根据图形所示填表：A的面积 + B的面积 = C的面积练习：
1、求下列图中字母所表示的正方形的面积议一议：（１）你能用三角形的边长表示正方形的面积吗？
（２）你能发现直角三角形三边的长度之间存在什么关系吗？
（３）分别以５厘米，１２厘米为直角边作出一个直角三角形，并测量斜边的长度．（２）中的规律对这个三角形仍然成立吗？
cab探究活动3：是否有与活动2同样的结论？正方形A的面积+正方形B的面积=正方形C的面积在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.千古第一定理数与形的第一定理导致第一次数学危机数学由计算转变为证明是第一个不定方程毕
达
哥
拉
斯
定
理勾股（商高）定理返 回正方形A的面积+正方形B的面积=正方形C的面积1.判断题:(1).如果三角形的三边长分别为a,b,c，则　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　　　　（　）
(2).如果直角三角形的三边长分别为a,b,c，则
　　　　　　　　　　　　　　　　　　　　　　　　　　（　）
××2.求出下列直角三角形中未知边的长度3.填空:(1).在△ABC中, ∠C=90°，c=25,b=15,则a=＿＿＿＿.
(2). 三角形的三个内角之比为：１：２：３，则此三角形是＿＿＿．若此三角形的三边长分别为a,b,c,则它们的关系是＿＿＿＿．
问题：在第(２)题中，如果把　１：２：３改成３：２：１，答案会一样吗？
２０直角三角形4. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少米? 想一想： 小明妈妈买了一部29英寸（74厘米）的电视机，小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你同意他的想法吗？你能解释这是为什么吗？定 理 的 历 史 及 证 明★ 公元前11世纪，周公与商高的对话（记录于公元前1世纪《周髀算经》）中提出“勾三、股四、弦五”。——勾股定理、商高定理★ 《周髀算经》中还记载了公元前六、七世纪的荣方与陈子的对话，再次提到勾股定理。——陈子定理★ 公元前600年左右，古希腊的毕达哥拉斯学派发现勾股定理，命名为“毕达哥拉斯定理” （百牛定理），而且给出了证明。★ 古巴比仑人在公元前19世纪也发现此定理。★ 中国最早给出定理证明的是公元3世纪三国时吴国数学家赵爽（赵君卿）。★ 定理从提出到现在的两千多年中，已经找到证明400多种，由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。证法一：（赵爽证法）正方形ABCD的面积为 还可以认为是四个三角形与一个小正方形的和，即∴ ∴证法二：（毕达哥拉斯证法） 如图，两个全等的正方形，双方都去掉四个全等带阴
影的直角三角形后，两正方形中剩下的部分面积应相等。
即：证法三：（伽菲尔德证法1876年） 如图，Rt△ABE≌Rt△ECD，
可知∠AED=90°；梯形ABCD的面积＝梯形ABCD的面积＝∴∴回忆与小结：１.这节课你的收获是什么？　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
２.理解“勾股定理”应该注意什么问题？
３.你觉得“勾股定理”有用吗？四、设计说明1、本节课是公式课，根据学生的知识结构，我采用的教学流程是：提出问题——实验操作——归纳验证——问题解决——课堂小结——布置作业等部分，这一流程体现了知识发生、形成和发展的过程，让学生体会到观察、猜想、归纳、验证的思想和数形结合的思想。
2、探索定理采用了面积法，引导学生利用实验由特殊到一般再到更一般的对直角三角形的三边关系的研究，得出结论。这种方法是认识事物规律的重要方法之，通过教学让学生初步掌握这种方法，对于学生良好思维品质的形成有重要作用，对于学生的终身发展也有一定的作用。
3、本课小结从内容、应用、数学思想方法，获取知识的途径等几个方面展开，既有知识的总结，又有方法的提炼，这样对于学生学知识，用知识是有很大的促进的