4.3用方程解决问题（5）

课件16张PPT。初中数学七年级上册
（苏科版）4.3 用方程解决实际问题(5)问题一：1．创设情境，引入新课回顾应用方程解决问题一般步骤？(1)审：审题,分析题中的已知量、未知量,明确它们之间的关系;
(2)找：找出能表示问题中全部含义的一个等量关系;
(3)设：设未知数(一般求什么就设什么)并写单位名称;
(4)列：根据等量关系列出方程;
(5)解：解所列出的方程，求出未知数的值;
(6)答：检验所求解是否符合题意,写出答案.问题二：1．创设情境，引入新课1、一项工程，甲独做需6天，乙独做需12天，把总工
作量看作1，两人合做一天的工作量是 ，
两人合做 天完成。2、一项工作，12个人4个小时才能完成。若这项工作
由8个人来做，要 小时才能完成。工作效率×工作时间＝工作总量问题三：2．合作质疑，探索新知 将一批会计报表输入电脑，甲单独做需
要20 h完成，乙单独做需要12 h完成，现
在先由甲单独做4h，剩下部分由甲、乙两
人合作完成，甲、乙两人合作的时间是多
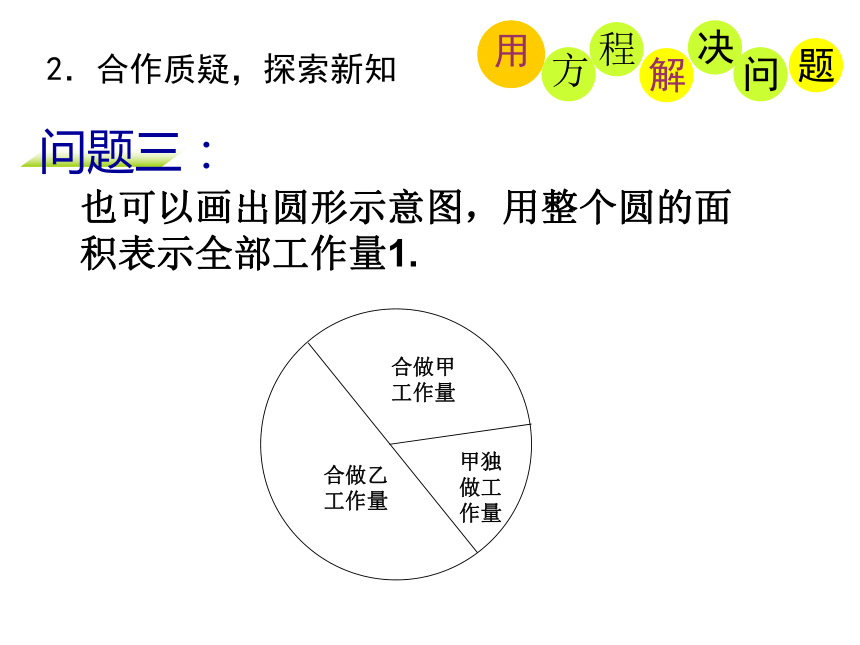
少？问题三：2．合作质疑，探索新知分析：这个问题中的相等关系是：全部工作量=甲单独做的工作量+甲、乙合做的工作量。如果把全部工作量看做1，设甲、乙两人合做的时间x小时，那么可以列出表格：2．合作质疑，探索新知问题三：也可以画出圆形示意图，用整个圆的面积表示全部工作量1.合做甲工作量合做乙工作量甲独做工作量问题三：2．合作质疑，探索新知解：设甲、乙两人合做的时间是x小时。根据题意，得解这个方程，得答：甲、乙两人合做的时间是6小时问题四：2．合作质疑，探索新知整理一批图书，由一个人做要40小时完
成，现在计划由若干人先做4小时，再增
加2人和他们一起做8小时，才完成这项工
作的 ，假设这些人的工作效率相
同，具体应先安排多少人工作？3．自主归纳，形成方法学生自主归纳：如何利用圆形图方法分析实际问题？(1)工程问题中的基本量及其关系:
工作量=工作效率×工作时间 (2)若问题中工作量未知,通常可把总工作量看作1，用圆形表示.(3)利用 各部分工作量之和等于总量 是工程问题中常用的等量关系.4.巩固练习1．某下水管道工程由甲、乙两个工程队单独铺设分别需要10天、15天完成.如果两队从两端同时施工2天，然后由乙队单独施工，还需多少天完成?2.整理一批图书，甲、乙两人单独做分别需要4h、6h完成.现在先由甲单独做1h，然后两人合作整理完这批图书，那么他们合作整理这批图书的时间是多少？3．一个蓄水池共有A，B两个进水管和一个排水管C．单独开A管，6小时可将空池注满水；单独开B管，10小时可将空池注满水；单独开C管，9小时可将满池水排完．现在水池中没有水．若先将A，B两管同时开2.5小时，然后打开C管，问打开C管后，几小时可将水池注满水？5．课堂小结，感悟收获通过以上问题的解决，你觉得如何利用圆形方法分析解决问题？
6．反思设计，分组活动有两支成分不同且长度相等的蜡烛，其中一支3小时可燃烧完，另一支4小时燃烧完．现在要求到下午四点钟时，其中一支蜡烛的剩余部分恰是另一支剩余部分的2倍，问应在何时点燃这两支蜡烛？7．发展能力，拓展延伸古希腊数学家丢番图的墓碑上记载着：“他生命的六分之一是幸福的童年；再活了他生命的十二分之一，两颊长起了细细的胡须；他结了婚，又度过了一生的七分之一；再过五年，他有了儿子，感到很幸福；可是儿子只活了他父亲全部年龄的一半；儿子死后，他在极度悲痛中度过了四年，也与世长辞了．”你知道丢番图结婚时和去世时的年龄分别是多少吗？拓展：甲、乙、丙三人合修一围墙，甲、乙合作6天完成工作量的1/3，然后乙、丙合作2天完成余下任务的1/4,剩余的工作三人合作5天才完成。他们共得900元，根据按劳分配的原则，每人应得多少钱？