1.3 平行四边形、矩形、菱形、正方形的性质与判定(7) 教学案
文档属性
| 名称 | 1.3 平行四边形、矩形、菱形、正方形的性质与判定(7) 教学案 |  | |
| 格式 | rar | ||
| 文件大小 | 28.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-04 17:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.3 平行四边形、矩形、菱形、正方形的性质与判定(7)
教学目标
1、会证明菱形的判定定理
2、能运用菱形的判定定理进行计算与证明
3、能运用菱形的性质定理与判定定理进行比较简单的综合推理与证明
教学重、难点
重点:菱形判定定理的证明
难点:菱形判定定理的应用
教学过程:
一、情境创设
具备什么条件的平行四边形是菱形?具备什么条件的四边形是菱形?同学之间进行交流。
二、探索活动
探索“对角线互相垂直的平行四边形是菱形”的证明思路。
问题一 如图,在□ABCD中,对角线AC、BD相交于点O,
且AC⊥BD,由此你可证得什么?(可得到两对全等的等腰三角形和
四个全等的直角三角形,还可得到AC、BD互相垂直平分)
问题二 如图,要证平行四边形ABCD是菱形,需证什么?为什么?
(要证平行四边形是菱形,根据菱形的定义,只需证一组邻边相等即可)
问题三 说说证明“对角线互相垂直的平行四边形是菱形”的思路。
(思路一:证相邻的两个直角三角形全等得出一组邻边相等即可;思路二:由垂直平分线的性质可得一组邻边相等。)
可选择思路二证明。
思考与探索 你能用直尺和圆规作一个菱形?并说明作图的理由。
作法一:可利用“四边相等的四边形是菱形”来作,先作一个角,再在角的两边上截取相等的边作为菱形的边长,再分别以两个截点为圆心,菱形的边长为半径画弧,两弧相交于一点,这点即为菱形的第四个顶点;
作法二:可利用“对角线互相垂直平分的四边形是菱形”来作,可先作出两条互相垂直平分的线段,再将两条线段的四个端点顺次连结起来,即作出了一个菱形。
例1、 已知:如图,在△ABC中,∠ABC=90°,AD是角平分线,点E、F分别在AC、AD上,且AE=AB,EF∥BC。
求证:四边形CDEF是菱形。
分析:由已知AD为角平分线,AE=AB联想到“三线合一”,
因此连结BE,可得到四边形BDEF的对角线互相垂直,只需证
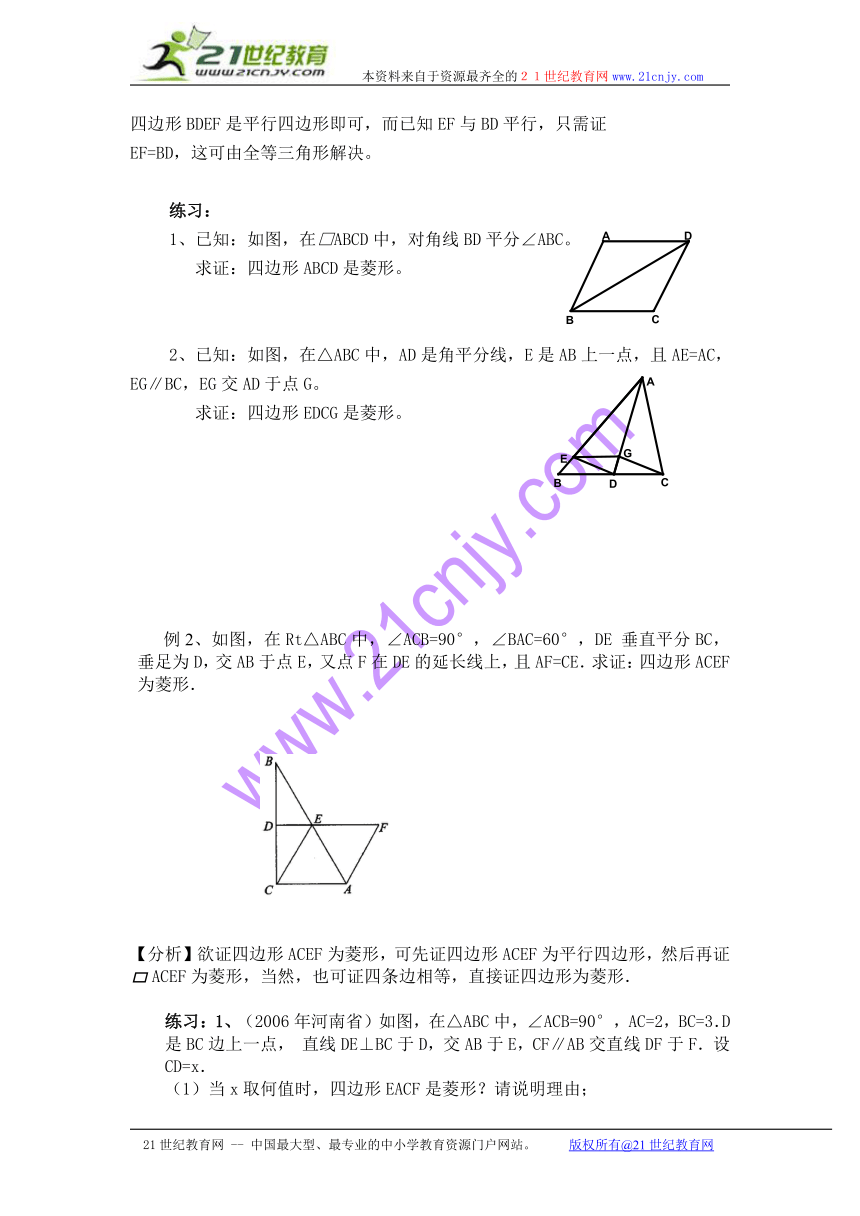
四边形BDEF是平行四边形即可,而已知EF与BD平行,只需证
EF=BD,这可由全等三角形解决。
练习:
1、已知:如图,在□ABCD中,对角线BD平分∠ABC。
求证:四边形ABCD是菱形。
2、已知:如图,在△ABC中,AD是角平分线,E是AB上一点,且AE=AC,EG∥BC,EG交AD于点G。
求证:四边形EDCG是菱形。
例2、如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E,又点F在DE的延长线上,且AF=CE.求证:四边形ACEF为菱形.
【分析】欲证四边形ACEF为菱形,可先证四边形ACEF为平行四边形,然后再证ACEF为菱形,当然,也可证四条边相等,直接证四边形为菱形.
练习:1、(2006年河南省)如图,在△ABC中,∠ACB=90°,AC=2,BC=3.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DF于F.设CD=x.
(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACD的面积等于2?
2.如图,点E、F是菱形ABCD的边BC、CD上的点,请你添加一个条件(不得另外添加辅助线和字母),使AE=AF,你添加的条件是________.
四、分层训练
1、判断
(1)对角线互相垂直的四边形是菱形。( )
(2)对角线互相平分的四边形是菱形。( )
(3)两组对边分别平行,且对角线 的四边形是菱形。
(4)两组对边分别相等,且对角线互相垂直的四边形是菱形。( )
2、(1)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
3、、已知:如图,AD是△ABC的角平分线,DE∥AC交AB于点E,
DF∥AB交AC于点F,请判断四边形AEDF的形状,并说明理由。
4、已知:如图,□ABCD的对角线AC的垂直平分线与边AD、BC
分别相交于点E、F。
求证:四边形AFCE是菱形。
5、将一张长方形纸片既快又准确地剪出一个菱形,并说出这样剪的依据。
五.目标检测
六、小结
1、 用直尺和圆规作一个菱形,并说明作图依据。
2、 菱形的判定方法。
七、教后感
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.3 平行四边形、矩形、菱形、正方形的性质与判定(7)
教学目标
1、会证明菱形的判定定理
2、能运用菱形的判定定理进行计算与证明
3、能运用菱形的性质定理与判定定理进行比较简单的综合推理与证明
教学重、难点
重点:菱形判定定理的证明
难点:菱形判定定理的应用
教学过程:
一、情境创设
具备什么条件的平行四边形是菱形?具备什么条件的四边形是菱形?同学之间进行交流。
二、探索活动
探索“对角线互相垂直的平行四边形是菱形”的证明思路。
问题一 如图,在□ABCD中,对角线AC、BD相交于点O,
且AC⊥BD,由此你可证得什么?(可得到两对全等的等腰三角形和
四个全等的直角三角形,还可得到AC、BD互相垂直平分)
问题二 如图,要证平行四边形ABCD是菱形,需证什么?为什么?
(要证平行四边形是菱形,根据菱形的定义,只需证一组邻边相等即可)
问题三 说说证明“对角线互相垂直的平行四边形是菱形”的思路。
(思路一:证相邻的两个直角三角形全等得出一组邻边相等即可;思路二:由垂直平分线的性质可得一组邻边相等。)
可选择思路二证明。
思考与探索 你能用直尺和圆规作一个菱形?并说明作图的理由。
作法一:可利用“四边相等的四边形是菱形”来作,先作一个角,再在角的两边上截取相等的边作为菱形的边长,再分别以两个截点为圆心,菱形的边长为半径画弧,两弧相交于一点,这点即为菱形的第四个顶点;
作法二:可利用“对角线互相垂直平分的四边形是菱形”来作,可先作出两条互相垂直平分的线段,再将两条线段的四个端点顺次连结起来,即作出了一个菱形。
例1、 已知:如图,在△ABC中,∠ABC=90°,AD是角平分线,点E、F分别在AC、AD上,且AE=AB,EF∥BC。
求证:四边形CDEF是菱形。
分析:由已知AD为角平分线,AE=AB联想到“三线合一”,
因此连结BE,可得到四边形BDEF的对角线互相垂直,只需证
四边形BDEF是平行四边形即可,而已知EF与BD平行,只需证
EF=BD,这可由全等三角形解决。
练习:
1、已知:如图,在□ABCD中,对角线BD平分∠ABC。
求证:四边形ABCD是菱形。
2、已知:如图,在△ABC中,AD是角平分线,E是AB上一点,且AE=AC,EG∥BC,EG交AD于点G。
求证:四边形EDCG是菱形。
例2、如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于点E,又点F在DE的延长线上,且AF=CE.求证:四边形ACEF为菱形.
【分析】欲证四边形ACEF为菱形,可先证四边形ACEF为平行四边形,然后再证ACEF为菱形,当然,也可证四条边相等,直接证四边形为菱形.
练习:1、(2006年河南省)如图,在△ABC中,∠ACB=90°,AC=2,BC=3.D是BC边上一点,直线DE⊥BC于D,交AB于E,CF∥AB交直线DF于F.设CD=x.
(1)当x取何值时,四边形EACF是菱形?请说明理由;
(2)当x取何值时,四边形EACD的面积等于2?
2.如图,点E、F是菱形ABCD的边BC、CD上的点,请你添加一个条件(不得另外添加辅助线和字母),使AE=AF,你添加的条件是________.
四、分层训练
1、判断
(1)对角线互相垂直的四边形是菱形。( )
(2)对角线互相平分的四边形是菱形。( )
(3)两组对边分别平行,且对角线 的四边形是菱形。
(4)两组对边分别相等,且对角线互相垂直的四边形是菱形。( )
2、(1)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
3、、已知:如图,AD是△ABC的角平分线,DE∥AC交AB于点E,
DF∥AB交AC于点F,请判断四边形AEDF的形状,并说明理由。
4、已知:如图,□ABCD的对角线AC的垂直平分线与边AD、BC
分别相交于点E、F。
求证:四边形AFCE是菱形。
5、将一张长方形纸片既快又准确地剪出一个菱形,并说出这样剪的依据。
五.目标检测
六、小结
1、 用直尺和圆规作一个菱形,并说明作图依据。
2、 菱形的判定方法。
七、教后感
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
