1.3 平行四边形、矩形、菱形、正方形的性质与判定(2) 教学案
文档属性
| 名称 | 1.3 平行四边形、矩形、菱形、正方形的性质与判定(2) 教学案 |

|
|
| 格式 | rar | ||
| 文件大小 | 59.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-04 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.3 平行四边形、矩形、菱形、正方形的性质与判定(2)
教学目标
1、认识几种特殊的四边形的性质的联系与区别
2、会证明矩形的性质定理及直角三角形斜边上中线的有关性质定理
3、能运用矩形的性质定理或有关定理进行简单的计算与证明
4、在进行探索、猜想、证明的过程中,能将命题由文字语言转化为图形与符号语言,进一步发展推理论证的能力
教学重、难点
重点:矩形的本质属性
难点:矩形性质定理的综合应用
教学过程:
一、情境创设
矩形是特殊的平行四边形,它具有平行四边形的所有性质。结合下图说说矩形有哪些平行四边形不具有的特殊性质?
你能证明这些性质吗?
二、合作交流
问题一 观察平行四边形和矩形的对角线把它们所分成的三角形,你有何发现?(引导学生不断地学会从多个角度观察、认识图形,主动地发现和获得新的数学结论,不断地积累数学活动的经验)
问题二 证明:矩形的4个角都是直角。
矩形的对角线相等。
问题三 你能证明“直角三角形斜边上的中线等于斜边的一半”吗?说说你的证明思路。
已知:如图,在△ABC中,∠ACB=90°.
求证:边AB上的中线等于AB.
证明:在∠ACB内作∠BCD=∠B,CD交AB于点D
∵∠ACB=90°
∴ACD与BCD互余,∠A与∠B互余
∵∠BCD=∠B
∴∠ACD=∠A
∴DA=DC=DB,即CD是边AB上的中线,且CD=AB
问题四 你对上面的结论还有更多的思考和猜想吗?(引导学生不断学会思考和猜想:由结论进一步能得到什么结论?这个结论的逆命题是否正确。不断发展学生数学思考的能力)
例1 、已知:如图,矩形ABCD的两条对角线相交于点O,
且AC=2AB.
求证:△AOB是等边三角形
分析:利用矩形的性质:矩形的对角线相等且互相平分,结合“AC=2AB”即可证得。
本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
练习:P16页 1、2
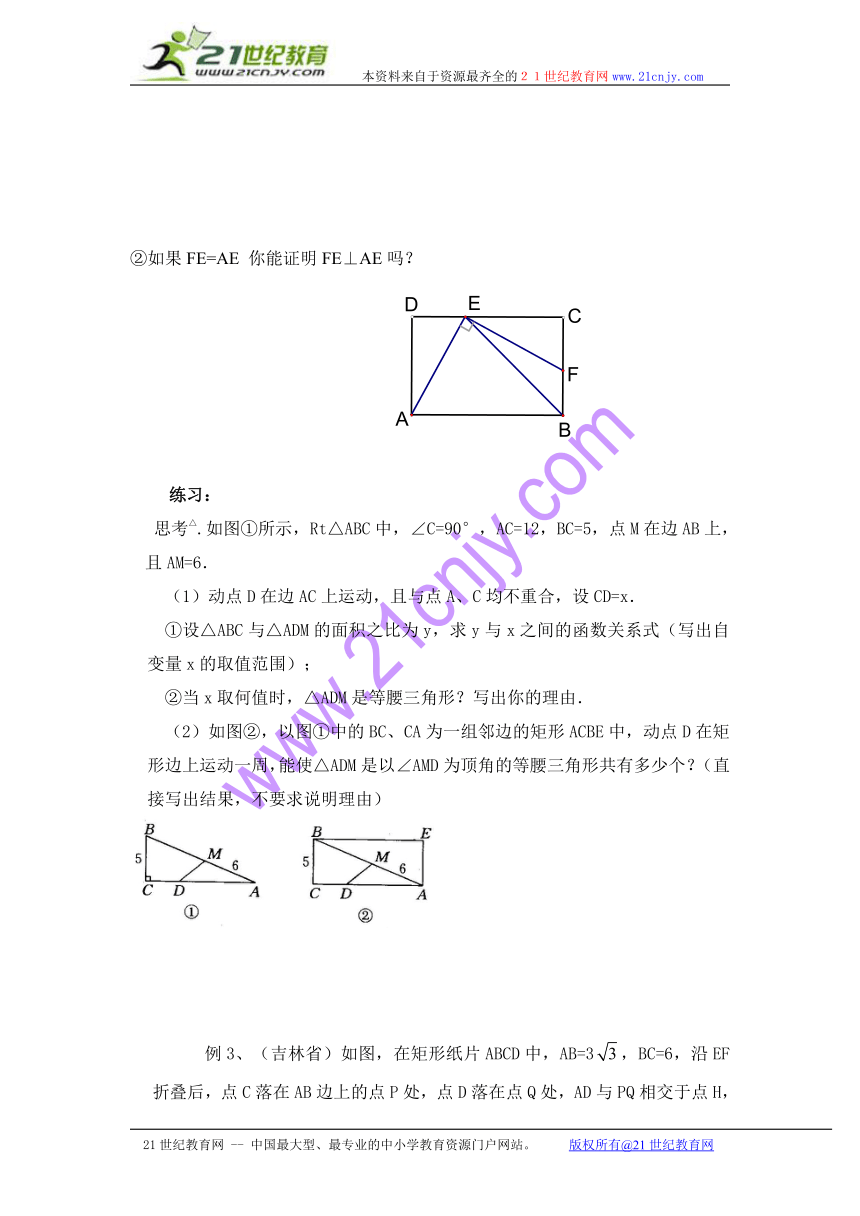
例2、如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
1 如果FE⊥AE,求证FE=AE。
②如果FE=AE 你能证明FE⊥AE吗?
练习:
思考△.如图①所示,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
(1)动点D在边AC上运动,且与点A、C均不重合,设CD=x.
①设△ABC与△ADM的面积之比为y,求y与x之间的函数关系式(写出自变量x的取值范围);
②当x取何值时,△ADM是等腰三角形?写出你的理由.
(2)如图②,以图①中的BC、CA为一组邻边的矩形ACBE中,动点D在矩形边上运动一周,能使△ADM是以∠AMD为顶角的等腰三角形共有多少个?(直接写出结果,不要求说明理由)
例3、(吉林省)如图,在矩形纸片ABCD中,AB=3,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°.
(1)求BE、QF的长.(2)求四边形PEFH的面积.
【分析】折叠型试题是近年中考试题的热点,要想解好此类题,考生必须有想像力,抓住折叠的角与边不发生变化,必要时需要考生剪一个四边形实际折叠一下帮助理解.
四、分层训练
1、已知,在矩形ABCD中,AE⊥BD,E是垂足,
∠DAE∶∠EAB=2∶1,求∠CAE的度数。
2、 在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
3、如图1,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( ).
(A)98 (B)196 (C)280 (D)284
(1) (2) (3)
4、如图2,根据实际需要,要在矩形实验田里修一条公路(小路任何地方水平宽度都相等),则剩余实验田的面积为________.
5、如图3,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,则矩形ABCD的面积为_______cm2.
6、已知,如图,矩形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OB的中点.
(1)求证:△ADE≌△BCF;(2)若AD=4cm,AB=8cm,求OF的长.
7、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE,求CE的长.
8、阅读下列过程:
如图①,小肖过AB,CD的中点画直线EF,把矩形ABCD分割成甲、乙两部分.
如图②,小徐过A,C两点画直线AC,把矩形ABCD分割成丙、丁两部分.
回答下列问题:
(1)填空:S甲_____S乙,S丙_____S丁(填“〉”或“〈”或“=”);
(2)根据小肖、小徐的分割原理,你还能探索出其他的分割方法吗?请在图③中任意给出一种;
(3)由本题的操作过程,你发现了什么规律?
.9、(2006年烟台市)如图4,先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如图①所示),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图②所示),若AB=4,BC=3,则图①和图②中,点B的坐标为_________,点C的坐标为________.
五、小结
从位置、形状、大小等不同的角度,观察和比较平行四边形、矩形的对角线把它们分成的三角形的异同,发现并应用直角三角形的判定证明矩形的特殊性质;反过来,我们又利用矩形的性质证明“直角三角形中斜边上的中线等于斜边的一半”。
六、课堂检测
七、教后感
A
B
D
C
E
O
① ②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.3 平行四边形、矩形、菱形、正方形的性质与判定(2)
教学目标
1、认识几种特殊的四边形的性质的联系与区别
2、会证明矩形的性质定理及直角三角形斜边上中线的有关性质定理
3、能运用矩形的性质定理或有关定理进行简单的计算与证明
4、在进行探索、猜想、证明的过程中,能将命题由文字语言转化为图形与符号语言,进一步发展推理论证的能力
教学重、难点
重点:矩形的本质属性
难点:矩形性质定理的综合应用
教学过程:
一、情境创设
矩形是特殊的平行四边形,它具有平行四边形的所有性质。结合下图说说矩形有哪些平行四边形不具有的特殊性质?
你能证明这些性质吗?
二、合作交流
问题一 观察平行四边形和矩形的对角线把它们所分成的三角形,你有何发现?(引导学生不断地学会从多个角度观察、认识图形,主动地发现和获得新的数学结论,不断地积累数学活动的经验)
问题二 证明:矩形的4个角都是直角。
矩形的对角线相等。
问题三 你能证明“直角三角形斜边上的中线等于斜边的一半”吗?说说你的证明思路。
已知:如图,在△ABC中,∠ACB=90°.
求证:边AB上的中线等于AB.
证明:在∠ACB内作∠BCD=∠B,CD交AB于点D
∵∠ACB=90°
∴ACD与BCD互余,∠A与∠B互余
∵∠BCD=∠B
∴∠ACD=∠A
∴DA=DC=DB,即CD是边AB上的中线,且CD=AB
问题四 你对上面的结论还有更多的思考和猜想吗?(引导学生不断学会思考和猜想:由结论进一步能得到什么结论?这个结论的逆命题是否正确。不断发展学生数学思考的能力)
例1 、已知:如图,矩形ABCD的两条对角线相交于点O,
且AC=2AB.
求证:△AOB是等边三角形
分析:利用矩形的性质:矩形的对角线相等且互相平分,结合“AC=2AB”即可证得。
本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
练习:P16页 1、2
例2、如图 在矩形ABCD中,BE平分∠ABC,交CD于点E,点F在边BC上,
1 如果FE⊥AE,求证FE=AE。
②如果FE=AE 你能证明FE⊥AE吗?
练习:
思考△.如图①所示,Rt△ABC中,∠C=90°,AC=12,BC=5,点M在边AB上,且AM=6.
(1)动点D在边AC上运动,且与点A、C均不重合,设CD=x.
①设△ABC与△ADM的面积之比为y,求y与x之间的函数关系式(写出自变量x的取值范围);
②当x取何值时,△ADM是等腰三角形?写出你的理由.
(2)如图②,以图①中的BC、CA为一组邻边的矩形ACBE中,动点D在矩形边上运动一周,能使△ADM是以∠AMD为顶角的等腰三角形共有多少个?(直接写出结果,不要求说明理由)
例3、(吉林省)如图,在矩形纸片ABCD中,AB=3,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°.
(1)求BE、QF的长.(2)求四边形PEFH的面积.
【分析】折叠型试题是近年中考试题的热点,要想解好此类题,考生必须有想像力,抓住折叠的角与边不发生变化,必要时需要考生剪一个四边形实际折叠一下帮助理解.
四、分层训练
1、已知,在矩形ABCD中,AE⊥BD,E是垂足,
∠DAE∶∠EAB=2∶1,求∠CAE的度数。
2、 在矩形ABCD中,对角线AC,BD相交于点O,若对角线AC=10cm,边BC=8cm,则△ABO的周长为________.
3、如图1,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( ).
(A)98 (B)196 (C)280 (D)284
(1) (2) (3)
4、如图2,根据实际需要,要在矩形实验田里修一条公路(小路任何地方水平宽度都相等),则剩余实验田的面积为________.
5、如图3,在矩形ABCD中,M是BC的中点,且MA⊥MD.若矩形ABCD的周长为48cm,则矩形ABCD的面积为_______cm2.
6、已知,如图,矩形ABCD的对角线AC,BD相交于点O,E,F分别是OA,OB的中点.
(1)求证:△ADE≌△BCF;(2)若AD=4cm,AB=8cm,求OF的长.
7、如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边的中点F处,折痕为AE,求CE的长.
8、阅读下列过程:
如图①,小肖过AB,CD的中点画直线EF,把矩形ABCD分割成甲、乙两部分.
如图②,小徐过A,C两点画直线AC,把矩形ABCD分割成丙、丁两部分.
回答下列问题:
(1)填空:S甲_____S乙,S丙_____S丁(填“〉”或“〈”或“=”);
(2)根据小肖、小徐的分割原理,你还能探索出其他的分割方法吗?请在图③中任意给出一种;
(3)由本题的操作过程,你发现了什么规律?
.9、(2006年烟台市)如图4,先将一矩形ABCD置于直角坐标系中,使点A与坐标系的原点重合,边AB、AD分别落在x轴、y轴上(如图①所示),再将此矩形在坐标平面内按逆时针方向绕原点旋转30°(如图②所示),若AB=4,BC=3,则图①和图②中,点B的坐标为_________,点C的坐标为________.
五、小结
从位置、形状、大小等不同的角度,观察和比较平行四边形、矩形的对角线把它们分成的三角形的异同,发现并应用直角三角形的判定证明矩形的特殊性质;反过来,我们又利用矩形的性质证明“直角三角形中斜边上的中线等于斜边的一半”。
六、课堂检测
七、教后感
A
B
D
C
E
O
① ②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
