北师版数学必修4单位圆与诱导公式
图片预览






文档简介
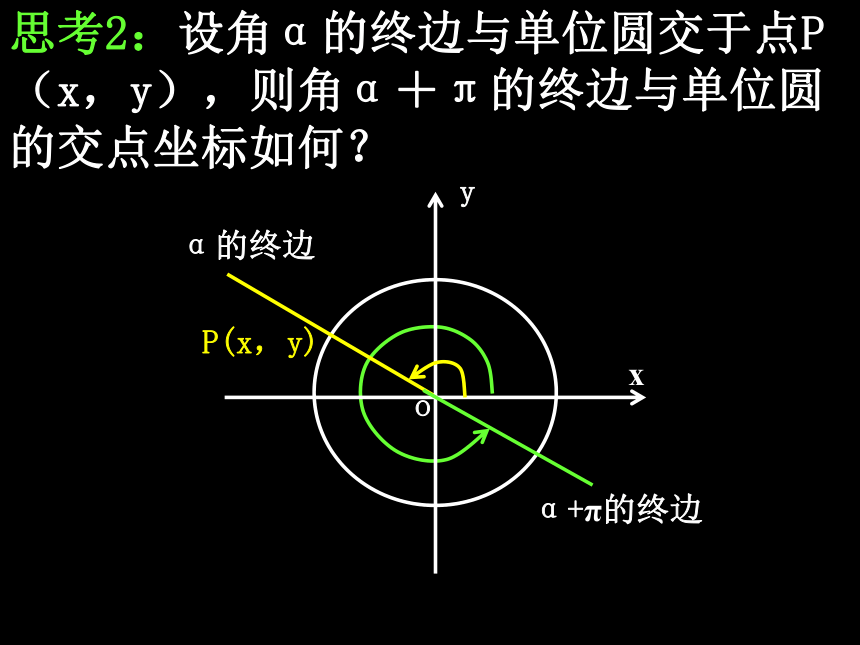
课件22张PPT。问题提出1.任意角α的正弦、余弦、正切是怎样定义的?2. 2kπ+α(k∈Z)与α的三角函数之间的关系是什么?3.你能求sin750°和sin930°的值吗?单位圆与诱导公式知识探究(一):α与α+π, α-π的 正余弦函数关系 思考1:对于任意给定的一个角α,角α+ π的终边与角α的终边有什么关系?思考2:设角α的终边与单位圆交于点P(x,y),则角α+π的终边与单位圆的交点坐标如何?思考3:根据三角函数定义,
sin( α +π) 、cos( α+π)、
tan( α +π )的值分别是什么?sin(α+π)=-ycos(α+π)=-xtan(α+π)=思考4:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系?思考5:α 与α-π的 正余弦函数关系 ?
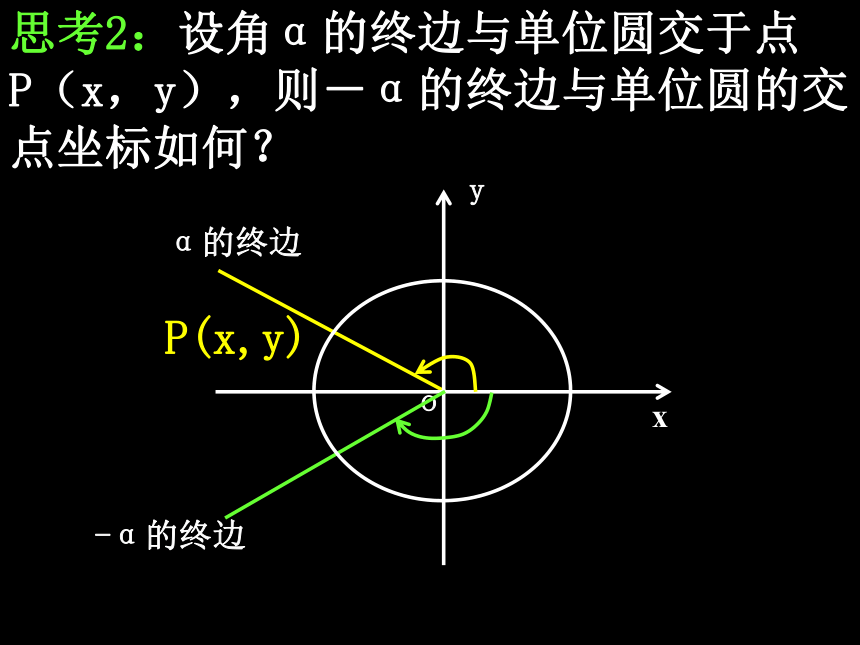
知识探究(二): α 与-α,π-α的正余弦函数关系思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何? 公式三: 思考3:根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考4:利用π-α=π+(-α),结合公式二、三,你能得到什么结论? 公式四: 思考5:如何根据三角函数定义推导公式四?P(x,y)思考6:公式三、四有什么特点,如何记忆?函数名不变,象限定符号 2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,再放上原函数的象限符号. 思考7:公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗? 理论迁移例1 求下列各三角函数的值:2.以诱导公式一~四为基础,还可以产生一些派生公式,
如sin(2π-α)=-sinα,
sin(3π-α)=sinα等.小结作业1.诱导公式都是恒等式,即在等式有意义时恒成立.3.利用诱导公式一~四,可以求任意角的三角函数,其基本思路是:这是一种化归与转化的数学思想.公式四公式一公式二,四,
五,六公式一公式二:公式一:公式三:公式四:公式六:公式五:思考 诱导公式可统一为
的三角函数与α的三角函数之间的关系,你有什么办法记住这些公式?奇变偶不变,符号看象限.例1 化简: 例2 已知 ,求
的值. 例3 化简:
(1) ;
(2) . 例2 化简:
(1) ;
(2) .
sin( α +π) 、cos( α+π)、
tan( α +π )的值分别是什么?sin(α+π)=-ycos(α+π)=-xtan(α+π)=思考4:对比sinα,cosα,tanα的值,π+α的三角函数与α的三角函数有什么关系?思考5:α 与α-π的 正余弦函数关系 ?
知识探究(二): α 与-α,π-α的正余弦函数关系思考2:设角α的终边与单位圆交于点 P(x,y),则-α的终边与单位圆的交点坐标如何? 公式三: 思考3:根据三角函数定义,-α的三角函数与α的三角函数有什么关系?思考4:利用π-α=π+(-α),结合公式二、三,你能得到什么结论? 公式四: 思考5:如何根据三角函数定义推导公式四?P(x,y)思考6:公式三、四有什么特点,如何记忆?函数名不变,象限定符号 2kπ+α(k∈Z),π+α,-α,π-α的三角函数值,等于α的同名函数值,再放上原函数的象限符号. 思考7:公式一~四都叫做诱导公式,他们分别反映了2kπ+α(k∈Z),π+α,-α,π-α的三角函数与α的三角函数之间的关系,你能概括一下这四组公式的共同特点和规律吗? 理论迁移例1 求下列各三角函数的值:2.以诱导公式一~四为基础,还可以产生一些派生公式,
如sin(2π-α)=-sinα,
sin(3π-α)=sinα等.小结作业1.诱导公式都是恒等式,即在等式有意义时恒成立.3.利用诱导公式一~四,可以求任意角的三角函数,其基本思路是:这是一种化归与转化的数学思想.公式四公式一公式二,四,
五,六公式一公式二:公式一:公式三:公式四:公式六:公式五:思考 诱导公式可统一为
的三角函数与α的三角函数之间的关系,你有什么办法记住这些公式?奇变偶不变,符号看象限.例1 化简: 例2 已知 ,求
的值. 例3 化简:
(1) ;
(2) . 例2 化简:
(1) ;
(2) .
