勾股定理
图片预览

文档简介
勾股定理(一)
学习目标:1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.2.培养在实际生活中发现问题总结规律的意识和能力.3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习.
学习重点、难点:勾股定理的内容及证明.
导学案:探究活动一:
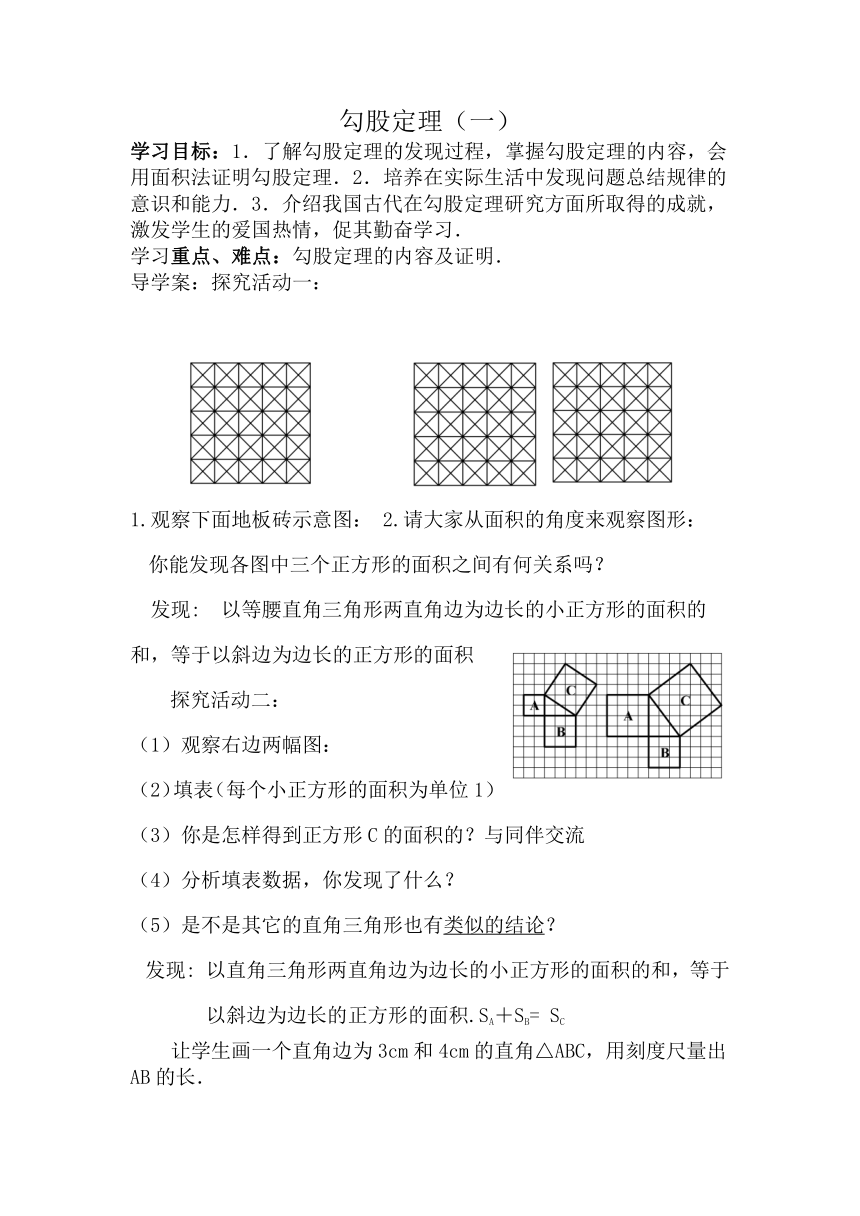
1.观察下面地板砖示意图: 2.请大家从面积的角度来观察图形:
你能发现各图中三个正方形的面积之间有何关系吗?
发现: 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积
探究活动二:
(1)观察右边两幅图:
(2)填表(每个小正方形的面积为单位1)
(3)你是怎样得到正方形C的面积的?与同伴交流
(4)分析填表数据,你发现了什么?
(5)是不是其它的直角三角形也有类似 ( H:\数学八下\几何画板勾股定理.gsp" \t "_parent )的结论?
发现: 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.SA+SB= SC
让学生画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出AB的长.
以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五.”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5.
再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长.
你是否发现32+42与52的关系,52+122和132的关系,即32+42=52,52+122=132,那么就有勾2+股2=弦2.
对于任意的直角三角形也有这个性质吗?
二、例习题分析
例1、已知:在△ABC中,∠C=90 ,∠A、∠B、∠C的对边为a、b、c.求证:a2+b2=c2.
分析:⑴让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明.
⑵拼成如图所示,其等量关系为:4S△+S小正=S大正
4×ab+(b-a)2=c2,化简可证.
⑶发挥学生的想象能力拼出不同的图形,进行证明.
⑷勾股定理的证明方法,达300余种.这个古老的精彩的证法,出自我国古代无名数学家之手.激发学生的民族自豪感,和爱国情怀.
例2、已知:在△ABC中,∠C=90 ,∠A、∠B、∠C的对边为a、b、c.求证:a2+b2=c2.
分析:左右两边的正方形边长相等,则两个正方形的面积相等.
左边S=4×ab+c2,右边S= (a+b)2
左边和右边面积相等,即4×ab+c2= (a+b)2,化简可证.
【设计意图】“赵爽证法”以教师讲解为主,学生参与分析为辅,让学生形成拼图意识,感受我国科学家的伟大发明,再通过设计“阅读与填空”,拓展学生的知识面,达到加深理解勾股定理的目的.
三、联系实际,应用所学
【显示投影片4】
问题探究1:一个门框的尺寸如课本图形18.1-4所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
思路点拨:从观察实验可知,木板横着进,竖着进,都无法从门框内通过,因此,尝试斜着通过,而对角线AC或BD是斜着能通过的最大长度.只要测出AC或BD,与木板的宽比较,就能知道木板是否能通过.
【活动方略】
教师活动:拿出教具:如图18.1-4的木框,几块木板,演示引导学生思考.
学生活动:观察、讨论,得到必须应用勾股定理求出木框的斜边AC2=AB2+BC2=12+22=5,AC=≈2.236,然后以此为尺寸,来判断薄木板能否通过木框,结论是可以!
问题探究2:如图18.1-5,一个3cm长的梯子,AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
思路点拨:从BD=OD-OB可以看出,必需先求OB,OD,因此,可以通过勾股定理在Rt△AOB,Rt△COD中求出OB和OD,最后将BD求出.
【活动方略】
教师活动:制作投影仪,提出问题,引导学生观察、应用勾股定理,提问个别学生.
学生活动:观察、交流,从中寻找出Rt△AOB,Rt△COD,以此为基础应用勾股定理求得OB和OD.
【课堂演练】
演练题:在Rt△ABC中,已知两直角边a与b的和为pcm,斜边长为qcm,求这个三角形的面积.
思路点拨:因为Rt△的面积等于ab,所以只要求出ab即可,由条件知a+b=p,c=q,联想勾股定理a2+b2=c2,将几何问题转化为代数问题.由a+b=p,a2+b2=q2求出ab.
教师活动:操作投影仪,组织学生演练,以练促思;引导学生进行等式变形.
学生活动:先独立思考,完成演练题1,再争取上台演示.
【设计意图】以两个探究为素材,帮助学生应用勾股定理,再通过设置的演练题来灵活学生的思维.
四、随堂练习,巩固深化
(1)若已知△ABC的两边分别为3和4,你能求出第三边吗?为什么?
(2)如图,已知:在△ABC,∠A=90°,D、E分别在AB、AC上,你能探究出CD2+BE2=BC2+DE2吗?
(提示:BE2+CD2=AD2+AC2+AB2+AE2=(AD2+AE2)+(AC2+AB2)=(DE2+BC2)
五、课堂总结,发展潜能
1.勾股定理:Rt△ABC中,∠C=90°,a2+b2=c2.
2.勾股定理适用于任何形状的直角三角形,在直角三角形中,已知任意两边的长都可以求出第三边的长.
六、布置作业,专题突破
1.课本P77 习题18.1 1,2,3,4,5.
学习目标:1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理.2.培养在实际生活中发现问题总结规律的意识和能力.3.介绍我国古代在勾股定理研究方面所取得的成就,激发学生的爱国热情,促其勤奋学习.
学习重点、难点:勾股定理的内容及证明.
导学案:探究活动一:
1.观察下面地板砖示意图: 2.请大家从面积的角度来观察图形:
你能发现各图中三个正方形的面积之间有何关系吗?
发现: 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积
探究活动二:
(1)观察右边两幅图:
(2)填表(每个小正方形的面积为单位1)
(3)你是怎样得到正方形C的面积的?与同伴交流
(4)分析填表数据,你发现了什么?
(5)是不是其它的直角三角形也有类似 ( H:\数学八下\几何画板勾股定理.gsp" \t "_parent )的结论?
发现: 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.SA+SB= SC
让学生画一个直角边为3cm和4cm的直角△ABC,用刻度尺量出AB的长.
以上这个事实是我国古代3000多年前有一个叫商高的人发现的,他说:“把一根直尺折成直角,两段连结得一直角三角形,勾广三,股修四,弦隅五.”这句话意思是说一个直角三角形较短直角边(勾)的长是3,长的直角边(股)的长是4,那么斜边(弦)的长是5.
再画一个两直角边为5和12的直角△ABC,用刻度尺量AB的长.
你是否发现32+42与52的关系,52+122和132的关系,即32+42=52,52+122=132,那么就有勾2+股2=弦2.
对于任意的直角三角形也有这个性质吗?
二、例习题分析
例1、已知:在△ABC中,∠C=90 ,∠A、∠B、∠C的对边为a、b、c.求证:a2+b2=c2.
分析:⑴让学生准备多个三角形模型,最好是有颜色的吹塑纸,让学生拼摆不同的形状,利用面积相等进行证明.
⑵拼成如图所示,其等量关系为:4S△+S小正=S大正
4×ab+(b-a)2=c2,化简可证.
⑶发挥学生的想象能力拼出不同的图形,进行证明.
⑷勾股定理的证明方法,达300余种.这个古老的精彩的证法,出自我国古代无名数学家之手.激发学生的民族自豪感,和爱国情怀.
例2、已知:在△ABC中,∠C=90 ,∠A、∠B、∠C的对边为a、b、c.求证:a2+b2=c2.
分析:左右两边的正方形边长相等,则两个正方形的面积相等.
左边S=4×ab+c2,右边S= (a+b)2
左边和右边面积相等,即4×ab+c2= (a+b)2,化简可证.
【设计意图】“赵爽证法”以教师讲解为主,学生参与分析为辅,让学生形成拼图意识,感受我国科学家的伟大发明,再通过设计“阅读与填空”,拓展学生的知识面,达到加深理解勾股定理的目的.
三、联系实际,应用所学
【显示投影片4】
问题探究1:一个门框的尺寸如课本图形18.1-4所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
思路点拨:从观察实验可知,木板横着进,竖着进,都无法从门框内通过,因此,尝试斜着通过,而对角线AC或BD是斜着能通过的最大长度.只要测出AC或BD,与木板的宽比较,就能知道木板是否能通过.
【活动方略】
教师活动:拿出教具:如图18.1-4的木框,几块木板,演示引导学生思考.
学生活动:观察、讨论,得到必须应用勾股定理求出木框的斜边AC2=AB2+BC2=12+22=5,AC=≈2.236,然后以此为尺寸,来判断薄木板能否通过木框,结论是可以!
问题探究2:如图18.1-5,一个3cm长的梯子,AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
思路点拨:从BD=OD-OB可以看出,必需先求OB,OD,因此,可以通过勾股定理在Rt△AOB,Rt△COD中求出OB和OD,最后将BD求出.
【活动方略】
教师活动:制作投影仪,提出问题,引导学生观察、应用勾股定理,提问个别学生.
学生活动:观察、交流,从中寻找出Rt△AOB,Rt△COD,以此为基础应用勾股定理求得OB和OD.
【课堂演练】
演练题:在Rt△ABC中,已知两直角边a与b的和为pcm,斜边长为qcm,求这个三角形的面积.
思路点拨:因为Rt△的面积等于ab,所以只要求出ab即可,由条件知a+b=p,c=q,联想勾股定理a2+b2=c2,将几何问题转化为代数问题.由a+b=p,a2+b2=q2求出ab.
教师活动:操作投影仪,组织学生演练,以练促思;引导学生进行等式变形.
学生活动:先独立思考,完成演练题1,再争取上台演示.
【设计意图】以两个探究为素材,帮助学生应用勾股定理,再通过设置的演练题来灵活学生的思维.
四、随堂练习,巩固深化
(1)若已知△ABC的两边分别为3和4,你能求出第三边吗?为什么?
(2)如图,已知:在△ABC,∠A=90°,D、E分别在AB、AC上,你能探究出CD2+BE2=BC2+DE2吗?
(提示:BE2+CD2=AD2+AC2+AB2+AE2=(AD2+AE2)+(AC2+AB2)=(DE2+BC2)
五、课堂总结,发展潜能
1.勾股定理:Rt△ABC中,∠C=90°,a2+b2=c2.
2.勾股定理适用于任何形状的直角三角形,在直角三角形中,已知任意两边的长都可以求出第三边的长.
六、布置作业,专题突破
1.课本P77 习题18.1 1,2,3,4,5.
