2.2.2椭圆的简单几何性质(二)
文档属性
| 名称 | 2.2.2椭圆的简单几何性质(二) |

|
|
| 格式 | rar | ||
| 文件大小 | 394.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-04 08:49:00 | ||
图片预览






文档简介
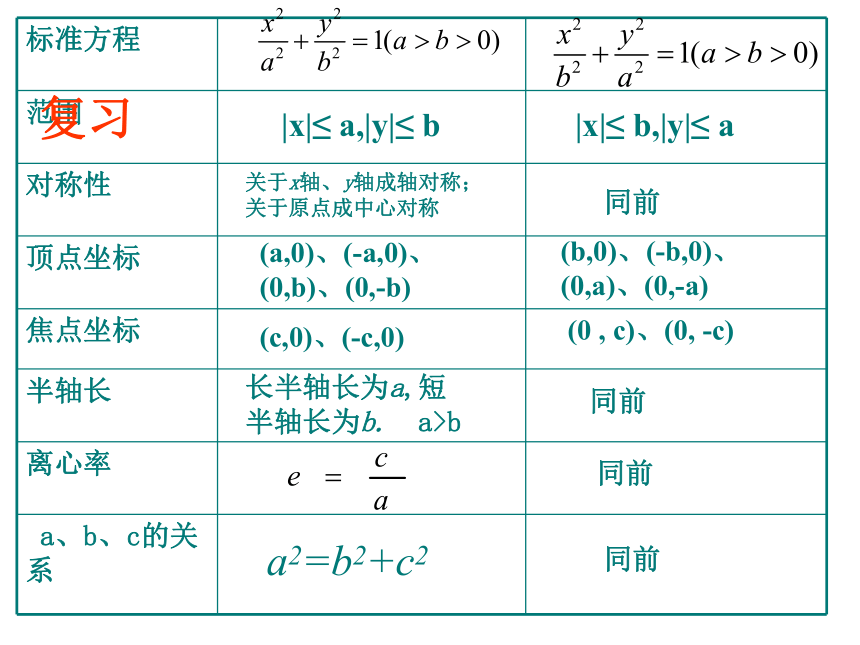
课件14张PPT。2.2.2椭圆的简单几何性质(二)|x|≤ a,|y|≤ b关于x轴、y轴成轴对称;关于原点成中心对称(a,0)、(-a,0)、(0,b)、(0,-b)(c,0)、(-c,0)长半轴长为a,短半轴长为b. a>ba2=b2+c2|x|≤ b,|y|≤ a同前(b,0)、(-b,0)、(0,a)、(0,-a)(0 , c)、(0, -c)同前同前同前复习课前练习求适合下列条件的椭圆的标准方程:
1.经过点P(-3,0) 、Q(0,-2);
2.长轴的长等于20,离心率等于例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1出发的光线,经过旋转椭圆面反射后集中到另一个焦点F2.解:建立如图所示的直角坐标系,
设所求椭圆方程为A所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。变式、点M(x,y)与定点F (c,0)的距离和它到定直线l:x=a2/c 的距离的比是常数c/a(a>c>0),求点M 的轨迹。yFF’lI’xoP={M| }由此得将上式两边平方,并化简,得设 a2-c2=b2,就可化成这是椭圆的标准方程,所以点M的轨迹是长轴、短轴分别为2a,2b 的椭圆M解:设 d是M到直线l 的距离,根据题意,所求轨迹就是集合y 由变式可知,当点M与一个定点的距离和它到一条定直
线的距离 的比是常数 时,这个点的轨
迹 就是椭圆,定点是椭圆的焦点,定直线叫做椭圆的准线,常数e是椭圆的离心率。 此为椭圆的第二定义.
对于椭圆 ,相应于焦点F(c,0)
准线方程是 , 根据椭圆的对称性,相应于
焦点F‘(-c.0) 准线方程是 ,
所以椭圆有两条准线。由椭圆的第二定义可得到椭圆的几何性质如下:设P(x0,y0)是椭圆 上的一点,F1(c,0), F2(c,0)分别是椭圆的左焦点、右焦点,我们把线段PF1,PF2的长分别叫做椭圆的左焦半径、右焦半径. 该公式的记忆方法为‘‘左加右减”,即在a与ex0之间,
如果是左焦半径则用加号“+’’连接,如果是右焦半径用“-”号连接. 焦半径公式
①焦点在x轴上时:
│PF1│=a+exo,│PF2│=a-exo;
②焦点在y轴上时: │PF1│=a+eyo,│PF2│=a-eyo。课堂练习
1、椭圆 上一点到准线 与到焦点(-2,0)的距离的比是 ( )B2、椭圆的两焦点把两准线间的距离三等分,则这个椭圆的离心率是( ) C3.若一个椭圆的离心率e=1/2, 准线方程是 x=4, 对应的焦点F(2,0),则椭圆的方程是 ____________3x2-8x+4y2=0例7.解:变式:
1.已知点M到定点F的距离与M到定直线l的距离的比为0.8,则动点M的轨迹是( )
A.圆 B.椭圆 C.直线 D.无法确定B小结 1. 椭圆的第二定义
2.焦半径:
①焦点在x轴上时:
│PF1│=a+ex0,│PF2│=a-ex0;
②焦点在y轴上时: │PF1│=a+ey0,│PF2│=a-ey0。
1.经过点P(-3,0) 、Q(0,-2);
2.长轴的长等于20,离心率等于例5 如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点F1上,片门位于另一个焦点F2上,由椭圆一个焦点F1出发的光线,经过旋转椭圆面反射后集中到另一个焦点F2.解:建立如图所示的直角坐标系,
设所求椭圆方程为A所以,点M的轨迹是长轴、短轴长分别为10、6的椭圆。变式、点M(x,y)与定点F (c,0)的距离和它到定直线l:x=a2/c 的距离的比是常数c/a(a>c>0),求点M 的轨迹。yFF’lI’xoP={M| }由此得将上式两边平方,并化简,得设 a2-c2=b2,就可化成这是椭圆的标准方程,所以点M的轨迹是长轴、短轴分别为2a,2b 的椭圆M解:设 d是M到直线l 的距离,根据题意,所求轨迹就是集合y 由变式可知,当点M与一个定点的距离和它到一条定直
线的距离 的比是常数 时,这个点的轨
迹 就是椭圆,定点是椭圆的焦点,定直线叫做椭圆的准线,常数e是椭圆的离心率。 此为椭圆的第二定义.
对于椭圆 ,相应于焦点F(c,0)
准线方程是 , 根据椭圆的对称性,相应于
焦点F‘(-c.0) 准线方程是 ,
所以椭圆有两条准线。由椭圆的第二定义可得到椭圆的几何性质如下:设P(x0,y0)是椭圆 上的一点,F1(c,0), F2(c,0)分别是椭圆的左焦点、右焦点,我们把线段PF1,PF2的长分别叫做椭圆的左焦半径、右焦半径. 该公式的记忆方法为‘‘左加右减”,即在a与ex0之间,
如果是左焦半径则用加号“+’’连接,如果是右焦半径用“-”号连接. 焦半径公式
①焦点在x轴上时:
│PF1│=a+exo,│PF2│=a-exo;
②焦点在y轴上时: │PF1│=a+eyo,│PF2│=a-eyo。课堂练习
1、椭圆 上一点到准线 与到焦点(-2,0)的距离的比是 ( )B2、椭圆的两焦点把两准线间的距离三等分,则这个椭圆的离心率是( ) C3.若一个椭圆的离心率e=1/2, 准线方程是 x=4, 对应的焦点F(2,0),则椭圆的方程是 ____________3x2-8x+4y2=0例7.解:变式:
1.已知点M到定点F的距离与M到定直线l的距离的比为0.8,则动点M的轨迹是( )
A.圆 B.椭圆 C.直线 D.无法确定B小结 1. 椭圆的第二定义
2.焦半径:
①焦点在x轴上时:
│PF1│=a+ex0,│PF2│=a-ex0;
②焦点在y轴上时: │PF1│=a+ey0,│PF2│=a-ey0。
