双曲线性质
图片预览





文档简介
课件27张PPT。双曲线的几何性质 关于x,y轴,
原点对称(±a,0),(0,±b)(±c,0)A1A2 ; B1B2 e =x =|x|?a,|y|≤b
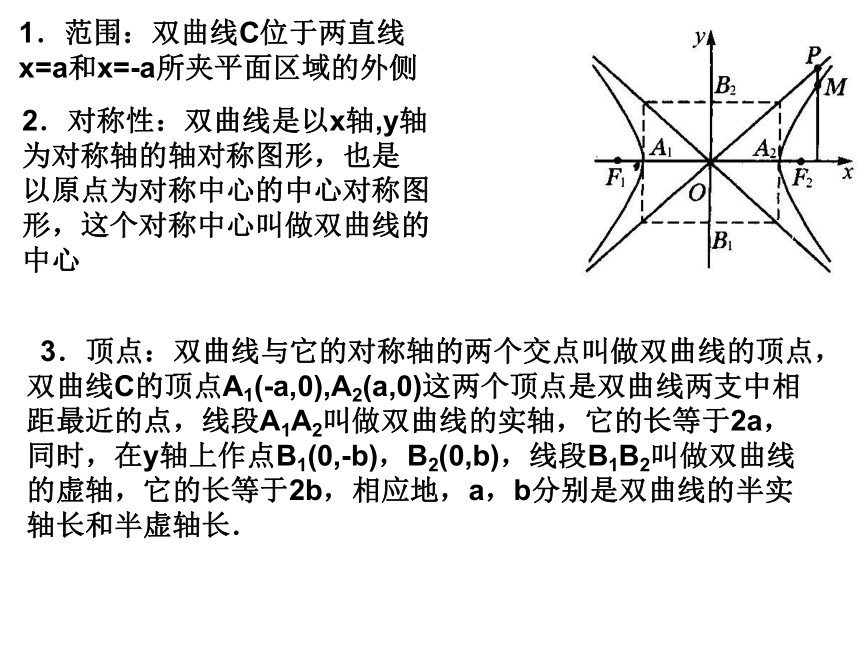
椭圆的图形与几何性质1.范围:双曲线C位于两直线
x=a和x=-a所夹平面区域的外侧2.对称性:双曲线是以x轴,y轴为对称轴的轴对称图形,也是
以原点为对称中心的中心对称图
形,这个对称中心叫做双曲线的
中心 3.顶点:双曲线与它的对称轴的两个交点叫做双曲线的顶点,双曲线C的顶点A1(-a,0),A2(a,0)这两个顶点是双曲线两支中相距最近的点,线段A1A2叫做双曲线的实轴,它的长等于2a,同时,在y轴上作点B1(0,-b),B2(0,b),线段B1B2叫做双曲线的虚轴,它的长等于2b,相应地,a,b分别是双曲线的半实轴长和半虚轴长.
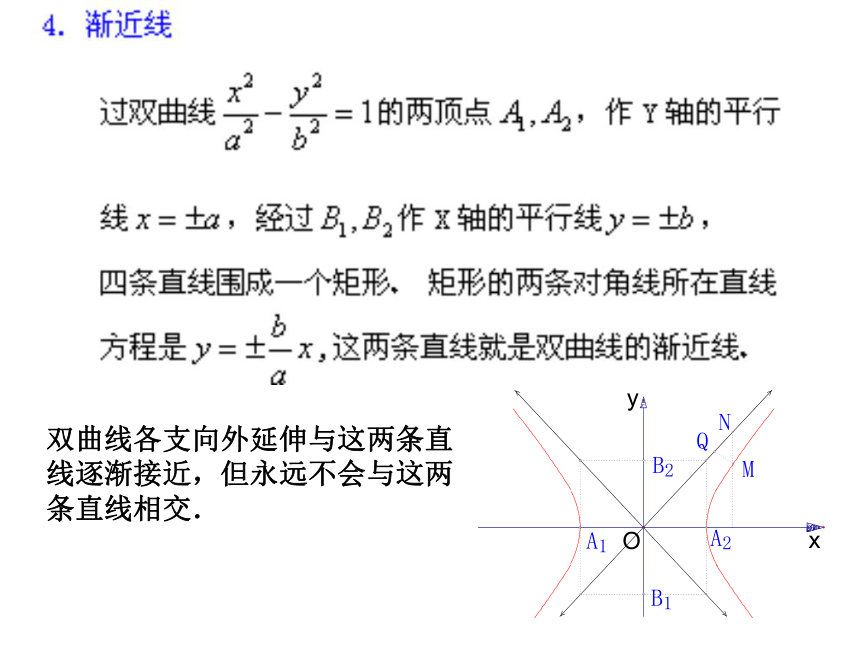
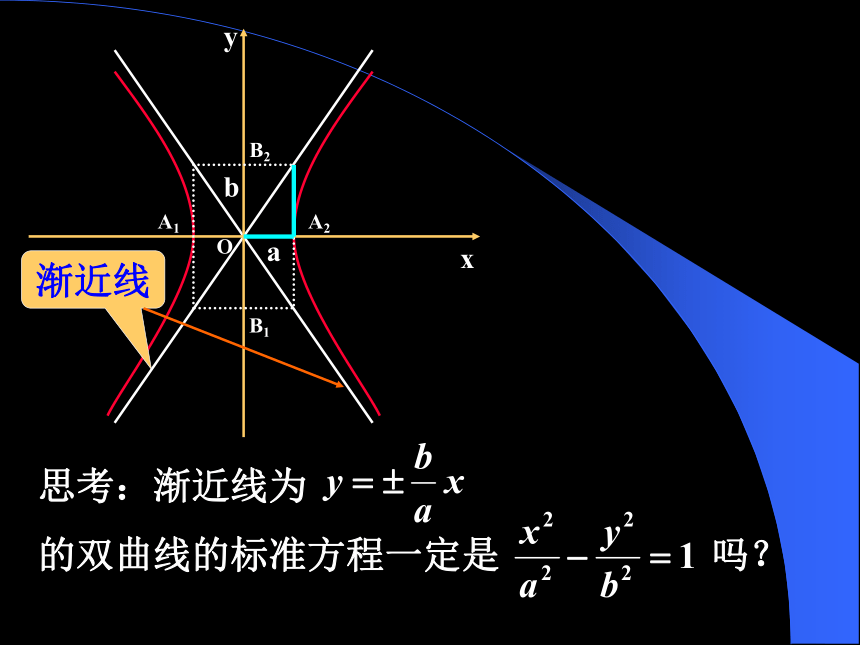
双曲线各支向外延伸与这两条直线逐渐接近,但永远不会与这两条直线相交.思考:渐近线为
的双曲线的标准方程一定是 吗?共轭双曲线:
________________________________________方程特征:
____________
____________
图象特征:
______________
______________以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线正负交换
其余不变有公共的渐近线
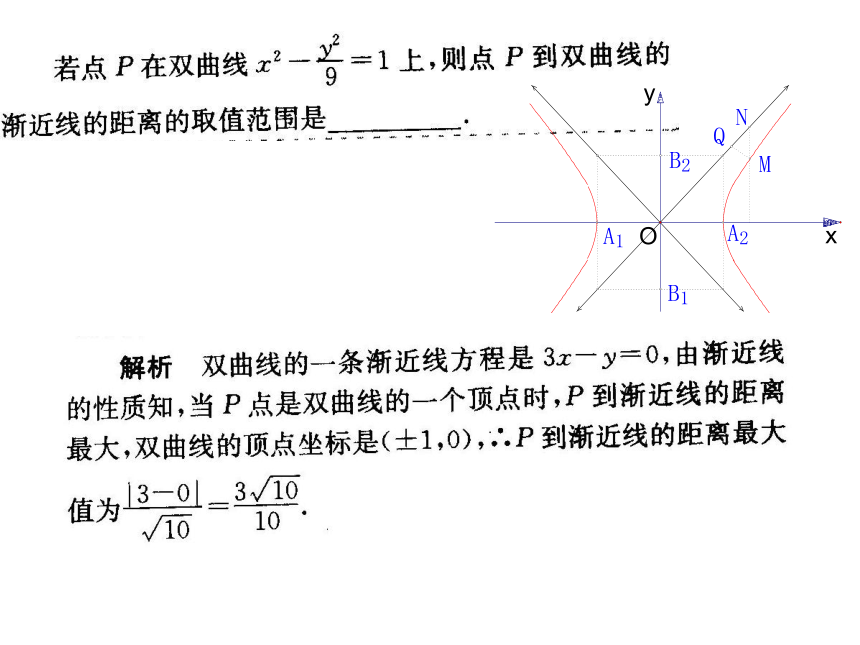
四焦点共圆例题1:求双曲线的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:即例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m。试选择适当的坐标系,求出此双曲线的方程(精确到1m).解:如图,建立直角坐标系xOy,使小圆的直径AA‘在x轴上,圆心与原点重合。这时,上下口的直径CC’,BB’都平行于x轴,且︱CC’ ︱=13×2, ︱BB’ ︱=25×2用计算器解方程,得b≈25一、选择题:ABCD一、选择题:ABCD一、选择题:ABCD一、选择题:ABCD二、填空题二、填空题二、填空题:二、填空题:小结(注意研究方法):1.范围
2.对称性
3.顶点,实轴 、虚轴
4.渐近线
5.离心率
作业
课本习题8.4第2(1)(2)(4),第4 题
YXF1F2A1A2B1B2双曲线图形(1)双曲线的图形与几何性质(1)双曲线标准方程:YX双曲线性质:1、范围:x≥a或x≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=XYF1F2OB1B2A2A1双曲线图形(2)双曲线的图形与几何性质(2)双曲线标准方程:YX双曲线性质:1、范围:y≥a或y≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:B1(0,-a),B2(0,a)4、轴:实轴 B1B2 ; 虚轴 A1A2A1A2B1B25、渐近线方程:6、离心率:e=c/aF2F2o例2:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原
双曲线的共轭双曲线,求证:
(1)双曲线和它的共轭双曲线有共同的渐近线;
(2)双曲线和它的共轭双曲线的四个焦点在同一个圆上.证明:(1)设已知双曲线的方程是:则它的共轭双曲线方程是:渐近线为渐近线为:显然,它可化为故双曲线和它的共轭双曲线有共同的渐近线;证明:(2)设已知双曲线的焦点为F(c,0),F(-c,0)它的共轭双曲线的焦点为F1’(0,c’), F2’(0,-c’),∵∴ c=c'∴四个焦点 , 在同一个圆YXA1A2B1B2F1F2oF’2F’1问:有相同渐近线的双曲线方
程一定是共轭双曲线吗一、选择题:ABCD
原点对称(±a,0),(0,±b)(±c,0)A1A2 ; B1B2 e =x =|x|?a,|y|≤b
椭圆的图形与几何性质1.范围:双曲线C位于两直线
x=a和x=-a所夹平面区域的外侧2.对称性:双曲线是以x轴,y轴为对称轴的轴对称图形,也是
以原点为对称中心的中心对称图
形,这个对称中心叫做双曲线的
中心 3.顶点:双曲线与它的对称轴的两个交点叫做双曲线的顶点,双曲线C的顶点A1(-a,0),A2(a,0)这两个顶点是双曲线两支中相距最近的点,线段A1A2叫做双曲线的实轴,它的长等于2a,同时,在y轴上作点B1(0,-b),B2(0,b),线段B1B2叫做双曲线的虚轴,它的长等于2b,相应地,a,b分别是双曲线的半实轴长和半虚轴长.
双曲线各支向外延伸与这两条直线逐渐接近,但永远不会与这两条直线相交.思考:渐近线为
的双曲线的标准方程一定是 吗?共轭双曲线:
________________________________________方程特征:
____________
____________
图象特征:
______________
______________以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线正负交换
其余不变有公共的渐近线
四焦点共圆例题1:求双曲线的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:即例4 双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m,上口半径为13m,下口半径为25m,高为55m。试选择适当的坐标系,求出此双曲线的方程(精确到1m).解:如图,建立直角坐标系xOy,使小圆的直径AA‘在x轴上,圆心与原点重合。这时,上下口的直径CC’,BB’都平行于x轴,且︱CC’ ︱=13×2, ︱BB’ ︱=25×2用计算器解方程,得b≈25一、选择题:ABCD一、选择题:ABCD一、选择题:ABCD一、选择题:ABCD二、填空题二、填空题二、填空题:二、填空题:小结(注意研究方法):1.范围
2.对称性
3.顶点,实轴 、虚轴
4.渐近线
5.离心率
作业
课本习题8.4第2(1)(2)(4),第4 题
YXF1F2A1A2B1B2双曲线图形(1)双曲线的图形与几何性质(1)双曲线标准方程:YX双曲线性质:1、范围:x≥a或x≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:A1(-a,0),A2(a,0)4、轴:实轴 A1A2 虚轴 B1B2A1A2B1B25、渐近线方程:6、离心率:e=XYF1F2OB1B2A2A1双曲线图形(2)双曲线的图形与几何性质(2)双曲线标准方程:YX双曲线性质:1、范围:y≥a或y≤-a
2、对称性:关于x轴,y轴,原点对称3、顶点:B1(0,-a),B2(0,a)4、轴:实轴 B1B2 ; 虚轴 A1A2A1A2B1B25、渐近线方程:6、离心率:e=c/aF2F2o例2:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线叫原
双曲线的共轭双曲线,求证:
(1)双曲线和它的共轭双曲线有共同的渐近线;
(2)双曲线和它的共轭双曲线的四个焦点在同一个圆上.证明:(1)设已知双曲线的方程是:则它的共轭双曲线方程是:渐近线为渐近线为:显然,它可化为故双曲线和它的共轭双曲线有共同的渐近线;证明:(2)设已知双曲线的焦点为F(c,0),F(-c,0)它的共轭双曲线的焦点为F1’(0,c’), F2’(0,-c’),∵∴ c=c'∴四个焦点 , 在同一个圆YXA1A2B1B2F1F2oF’2F’1问:有相同渐近线的双曲线方
程一定是共轭双曲线吗一、选择题:ABCD
