抛物线性质
图片预览





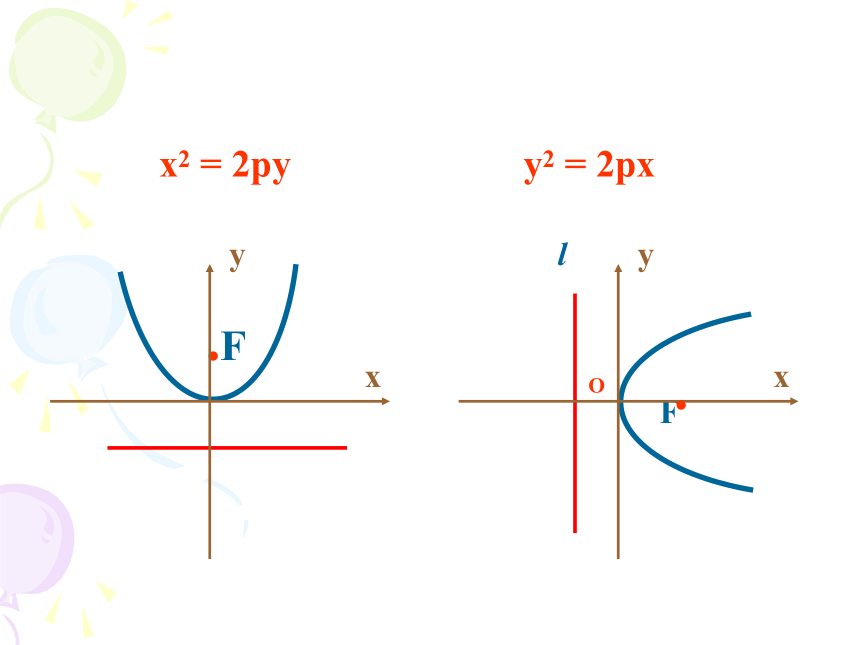
文档简介
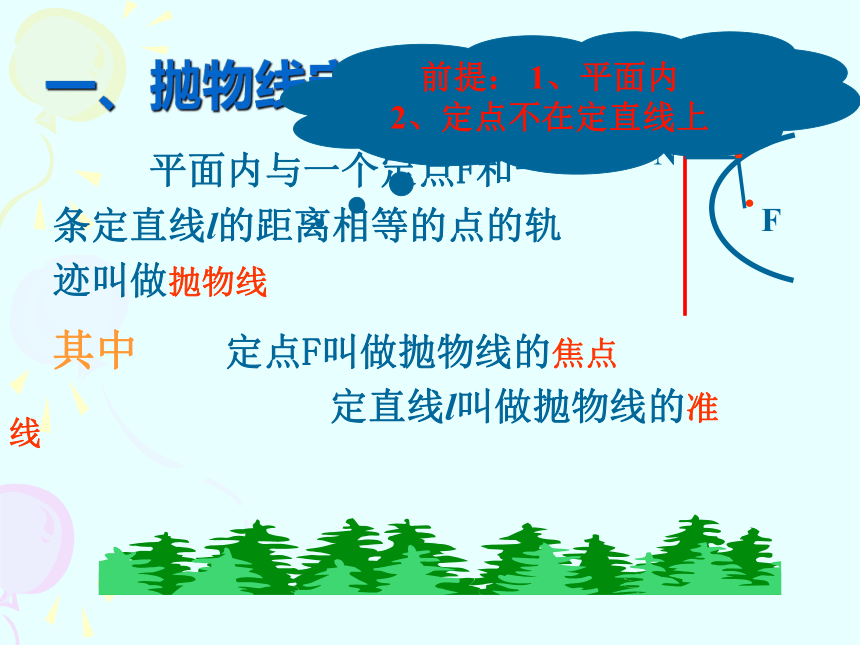
课件22张PPT。抛物线及其标准方程 与一个定点的距离和一条定直线的距离的比是常数 e的点的轨迹,当 0< e <1时是椭圆, 当 e >1时是双曲线, 当 e =1时是什么曲线呢? 引 入 平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线一、抛物线定义
其中 定点F叫做抛物线的焦点
定直线l叫做抛物线的准线前提: 1、平面内
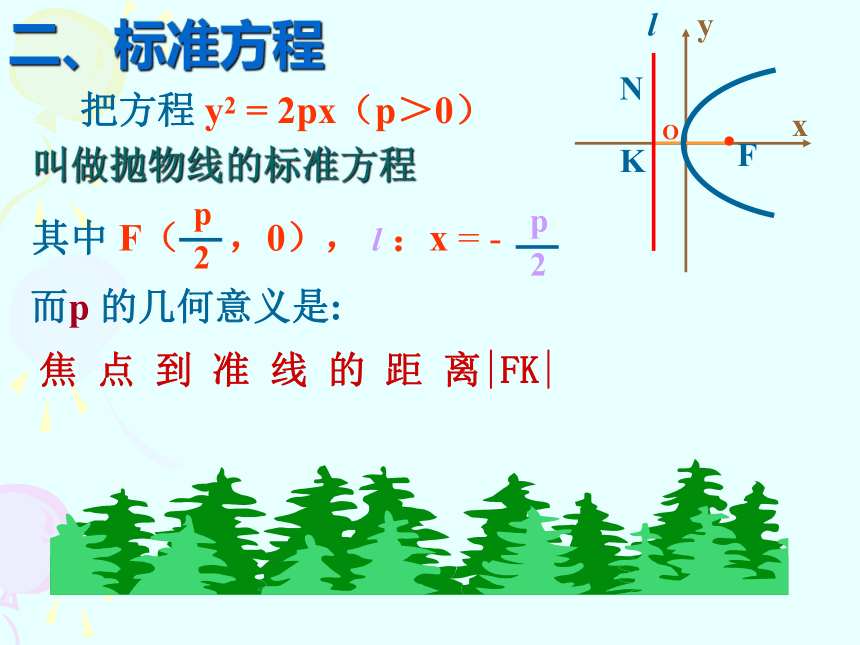
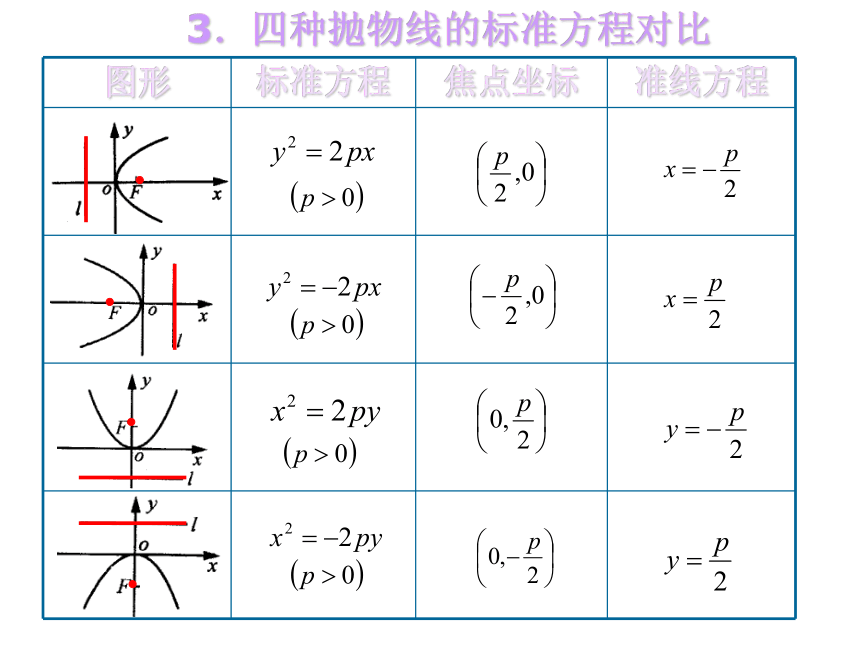
2、定点不在定直线上求曲线方程的基本步骤是怎样的?想一想?K回顾求曲线方程一般步骤:1、建系、设点2、写出适合条件P的点M的集合3、列方程4、化简5、(证明)K设︱KF︱= p设点M的坐标为(x,y), 由定义可知 |MF|=|MN| 即:解:设取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦 点 到 准 线 的 距 离|FK|其中二、标准方程y2 = 2pxx2 = 2py3.四种抛物线的标准方程对比 怎样把抛物线位置特征(标准位置)和方程的特点(标准方程)统一起来?顶点在原点焦点在
x轴上标准方程为
y2=+ 2px
(p>0)开口与x轴同向:
y2=+2px开口与x轴反向:
y =-2px焦点在
y轴上标准方程为
x =+ 2py
(p>0)开口与y轴同向:
x =+2py开口与y轴反向:
x =-2py已知抛物线标准方程,如何确定抛物线焦点位置及开口方向?一次项变量对应焦点所在轴,
开口方向看正负例1求下列抛物线的焦点坐标和准线方程
(1)y2=6x (2) (3)2x2+5y=0则焦点坐标是F(0,- ), 准线方程是y= (2)焦点坐标是 准线方程是例2根据下列条件写出抛物线的标准方程:
(1)焦点坐标是F(0,-2) (2)焦点在直线3x-4y-12=0上 (3) 抛物线过点A(-3,2)解: (1)抛物线的方程是x2=-8y(2)抛物线的方程是y2=16x或x2=-12y
(3)当抛物线的焦点在y轴的正半轴上时, 把A(-3,2)代入x2 =2py,当焦点在x轴的负半轴上时, 把A(-3,2)代入y2 = -2px,∴抛物线的标准方程为
x2 = y或y2 = - x练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是x = ;(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2思考题:抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?小 结 :1、学习了一个概念--抛物线2、掌握了一种题型--3、注重了一种思想--数形结合有关抛物线的标准方程和它的焦点坐标、准线方程的求法
探索 1.你能说出课本中作抛物线的方法的依据吗?2.如图:已知抛物线和它的准线,请你用尺规法作出它的焦点。作 业课本P64
习题A 2、3, B,1
其中 定点F叫做抛物线的焦点
定直线l叫做抛物线的准线前提: 1、平面内
2、定点不在定直线上求曲线方程的基本步骤是怎样的?想一想?K回顾求曲线方程一般步骤:1、建系、设点2、写出适合条件P的点M的集合3、列方程4、化简5、(证明)K设︱KF︱= p设点M的坐标为(x,y), 由定义可知 |MF|=|MN| 即:解:设取过焦点F且垂直于准线l的直线为x轴,线段KF的中垂线y轴 把方程 y2 = 2px(p>0) 叫做抛物线的标准方程而p 的几何意义是: 焦 点 到 准 线 的 距 离|FK|其中二、标准方程y2 = 2pxx2 = 2py3.四种抛物线的标准方程对比 怎样把抛物线位置特征(标准位置)和方程的特点(标准方程)统一起来?顶点在原点焦点在
x轴上标准方程为
y2=+ 2px
(p>0)开口与x轴同向:
y2=+2px开口与x轴反向:
y =-2px焦点在
y轴上标准方程为
x =+ 2py
(p>0)开口与y轴同向:
x =+2py开口与y轴反向:
x =-2py已知抛物线标准方程,如何确定抛物线焦点位置及开口方向?一次项变量对应焦点所在轴,
开口方向看正负例1求下列抛物线的焦点坐标和准线方程
(1)y2=6x (2) (3)2x2+5y=0则焦点坐标是F(0,- ), 准线方程是y= (2)焦点坐标是 准线方程是例2根据下列条件写出抛物线的标准方程:
(1)焦点坐标是F(0,-2) (2)焦点在直线3x-4y-12=0上 (3) 抛物线过点A(-3,2)解: (1)抛物线的方程是x2=-8y(2)抛物线的方程是y2=16x或x2=-12y
(3)当抛物线的焦点在y轴的正半轴上时, 把A(-3,2)代入x2 =2py,当焦点在x轴的负半轴上时, 把A(-3,2)代入y2 = -2px,∴抛物线的标准方程为
x2 = y或y2 = - x练习:1、根据下列条件,写出抛物线的标准方程:(1)焦点是F(3,0);(2)准线方程 是x = ;(3)焦点到准线的距离是2。y2 =12xy2 =xy2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4y2、求下列抛物线的焦点坐标和准线方程:
(1)y2 = 20x (2)x2= y
(3)2y2 +5x =0 (4)x2 +8y =0(5,0)x= -5(0,-2)y=2思考题:抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?
抛物线的方程为x=ay2(a≠0)求它的焦点坐标和准线方程?小 结 :1、学习了一个概念--抛物线2、掌握了一种题型--3、注重了一种思想--数形结合有关抛物线的标准方程和它的焦点坐标、准线方程的求法
探索 1.你能说出课本中作抛物线的方法的依据吗?2.如图:已知抛物线和它的准线,请你用尺规法作出它的焦点。作 业课本P64
习题A 2、3, B,1
