数轴

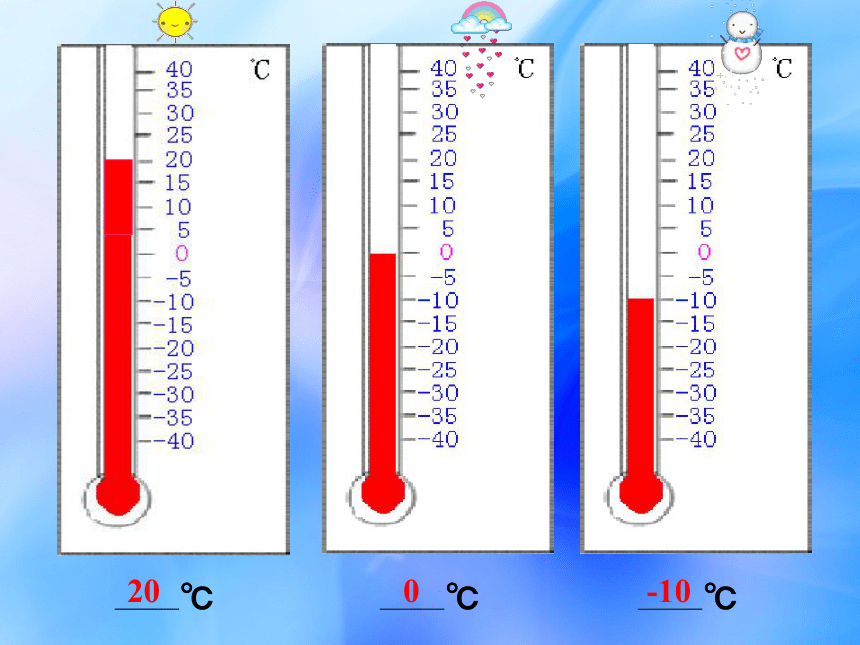
课件15张PPT。℃℃℃200-100510-10 -5
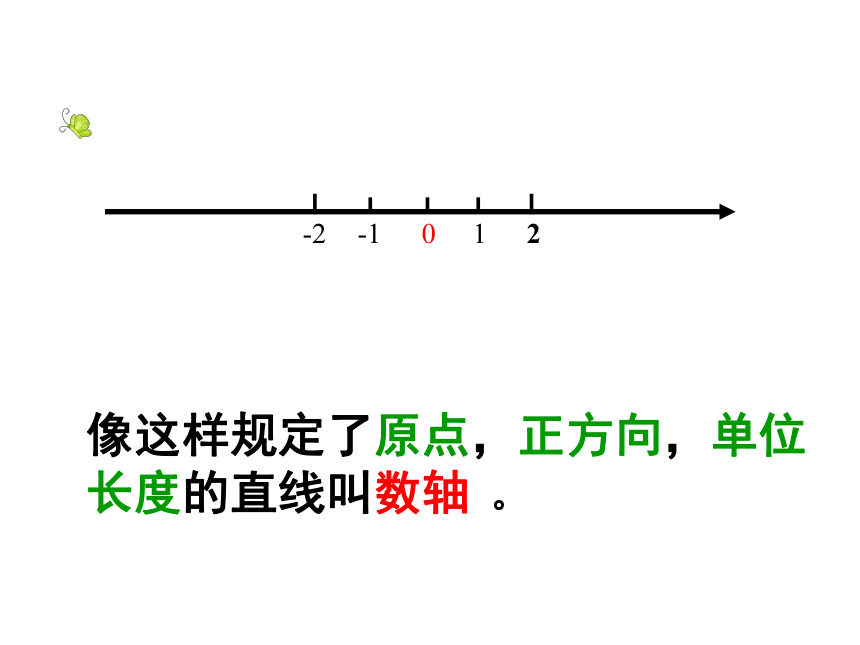
像这样规定了原点，正方向，单位长度的直线叫数轴 。 判断下面所画数轴是否正确，并说明理由。1.01-1错3.2.4.2-11错0错01-12对-2原点、正方向、单位长度一个也不能少。画数轴时要注意以下四点：⒈画水平直线；⒉在直线上取一点作为原点；⒊规定向右的方向为正方向，并用箭头表示；⒋根据需要选取适当单位长度。解：点A表示 -2；点B表示2；点D表示-1；点C表示0；例10123-1-2ADCB指出数轴上A，B，C，D各点分别表示什么数。例2 画一条数轴，在数轴上表示下列各数
　3.5，2，0，－2，－3.5观察上述的2与－2有什么相同点与不同点？它们在数轴上的位置有什么关系？3.5与－3.5呢？ 解：想一想：0-2-424-3-113任何一个有理数都可以用数轴上
的一个点来表示。
23.5-2-3.50相反数的概念：如果两个数只有符号不同，那么我们称其中一个数为另一个数的相反数，也称这两个数互为相反数，特别地，0的相反数是0。例3：求下列各数的相反数：
（1）－1　　（2）1.5　　　（3）0解：（1）－1的相反数是1（2）1.5的相反数是－1.5（3）0的相反数是0 在数轴上，表示互为相反数的两个点，位于原点的两侧，并与原点的距离相等。
数轴上两个点表示的数，右边的总比左边的大。负数小于0，正数大于负数。 正数大于0，越来越大例4　比较下列每组数的大小：
（1）－2和＋6；（2）0和－1.8；（3）－1.5和－4解：（1）－2＜＋6（正数大于负数）（2）0＞－1.8（负数小于零）（3）－1.5＞－4（在数轴上，－1.5所对应的点在－4所对应点的右侧）1）- 6的相反数是 ，5是 的相反数； 2）数轴上到原点的距离等于3个单位长度的点表示的数是___________________________；1 、 请你填一填：3）数a、b在数轴上的位置如图，则 b a（填“<”或“>”）6-53或－3<　随堂练习:? ?　 ? ? 1）在数轴上离表示数+2的点3个单位长度的数是5（ ）2）在数轴上离原点越远的点表示的数越大（ ）3）表示互为相反数的两个点到原点的距离相等（ 　）　　　4）一个数的相反数是它本身，这个数是1（ ）2、判断题：0+2 数轴的引入，使我们能用直观图形来研究数的有关概念，这就是“数”与“形”的结合，数形结合是一种重要数学的方法，我们应注意掌握。
1、明确数轴的三要素，即：原点、正方向和单位长度；
通过本节课的学习，你已掌握了哪些知识？2、能将已知数在数轴上表示出来，能说出数轴上已知点表示的数；
3、会比较数轴上数的大小；
4、掌握相反数的概念。祝同学们：学习进步！
快乐成长！