2.3.2双曲线的几何性质
图片预览



文档简介
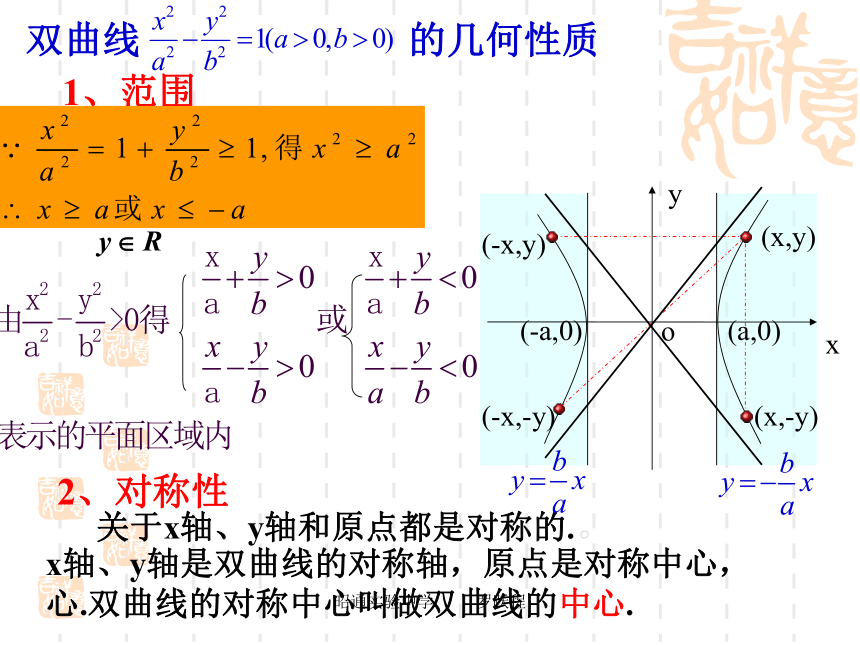
课件18张PPT。昭通实验中学 罗跃程2.3.2《双曲线的几何性质》昭通实验中学 罗跃程 2、对称性 双曲线 的几何性质1、范围关于x轴、y轴和原点都是对称的.。x轴、y轴是双曲线的对称轴,原点是对称中心,
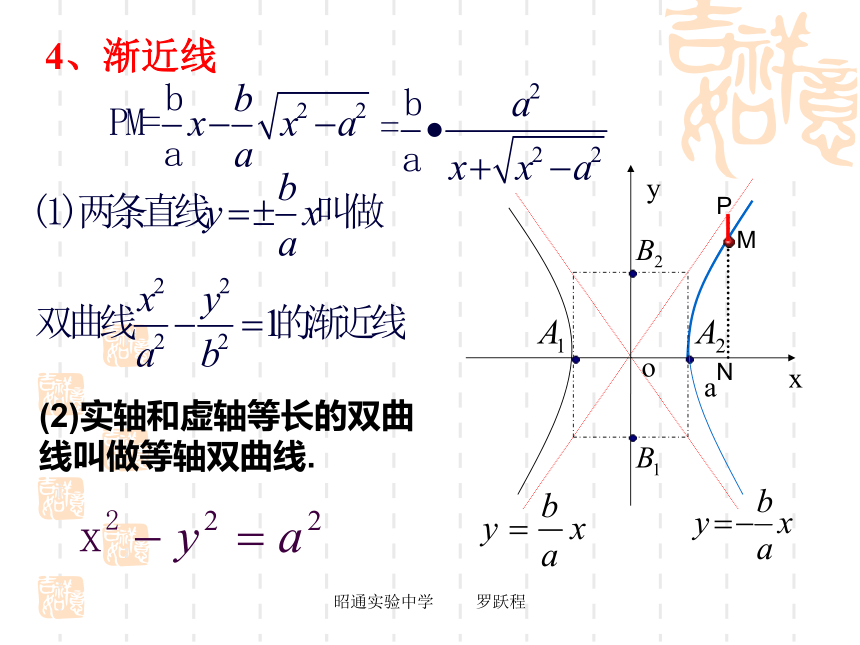
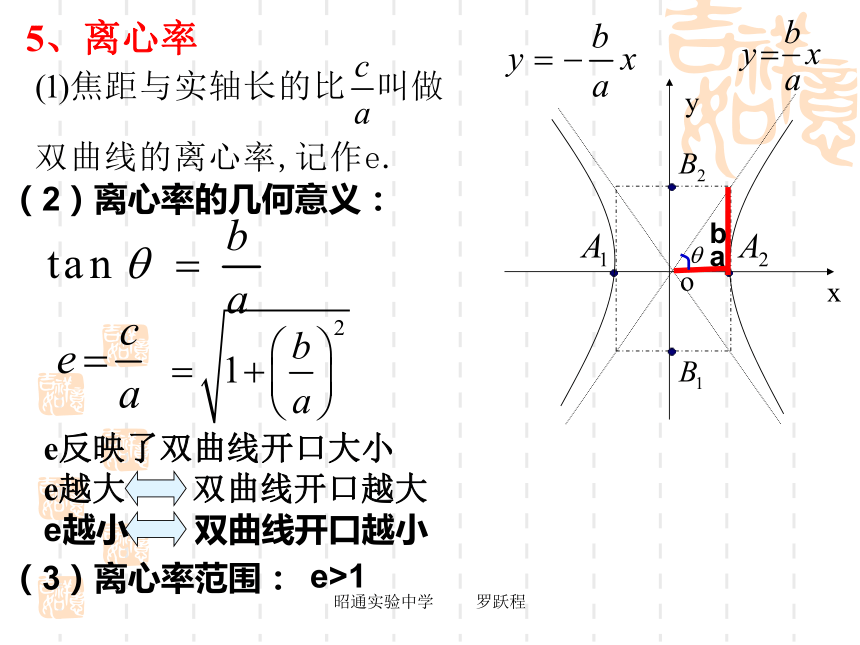
心.双曲线的对称中心叫做双曲线的中心.(-x,-y)(-x,y)(x,y)(x,-y)昭通实验中学 罗跃程3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点探究昭通实验中学 罗跃程a4、渐近线MNP(2)实轴和虚轴等长的双曲线叫做等轴双曲线.昭通实验中学 罗跃程5、离心率e反映了双曲线开口大小
e越大 双曲线开口越大
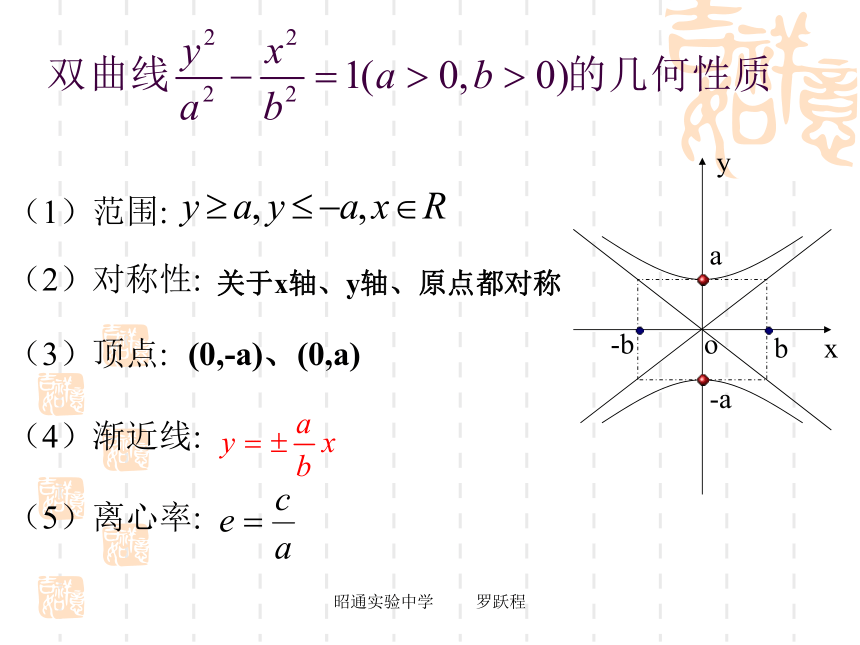
e越小 双曲线开口越小(3)离心率范围:(2)离心率的几何意义:e>1ab 昭通实验中学 罗跃程(1)范围:(2)对称性:关于x轴、y轴、原点都对称(3)顶点:(0,-a)、(0,a)(4)渐近线:(5)离心率:昭通实验中学 罗跃程例1 :求双曲线的实轴长、虚轴长、焦点坐标、顶点坐标、离心率、渐近线方程。解:由题意可得 实半轴长:虚轴长:焦点坐标:离心率:渐近线方程:例题选讲a=2顶点坐标:(-2,0),(2,0)请你写出一个以 为渐近线的双曲线方程. 你能写出所有以 为渐近线的
双曲线方程吗?相关练习昭通实验中学 罗跃程1、“共渐近线”的双曲线λ>0表示焦点在x轴上的双曲线;λ<0表示焦点在y轴上的双曲线。2、“共焦点”的双曲线(1)与椭圆 有共同焦点的双曲线方程表
示为(2)与双曲线 有共同焦点的双曲线方
程表示为昭通实验中学 罗跃程练习:3、求以椭圆 的焦点为顶点,以椭圆的
顶点为焦点的双曲线的方程。昭通实验中学 罗跃程例4、双曲线型冷却塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m). A′A0xC′CB′By例题讲解 昭通实验中学 罗跃程例5、点M(x,y)与定点F(5,0),的距离
和它到定直线 : 的距离的比是常
数 , 求点M的轨迹. y0d昭通实验中学 罗跃程昭通实验中学 罗跃程直线与双曲线问题:例6、如图,过双曲线 的右焦点
倾斜角为 的直线交双曲线于A,B两点,求|AB|。昭通实验中学 罗跃程43(0, -5) 、(0, 5)昭通实验中学 罗跃程2.双曲线的一条渐近线方程为 , 且过点 P (3, ), 则它的标准方程
是 . 昭通实验中学 罗跃程昭通实验中学 罗跃程问:若将题目中“焦点在y轴上”改为“焦点在坐标轴上”呢?先定型,再定量昭通实验中学 罗跃程课堂小结:
通过本节课的学习,你有哪些收获?ab(1)由双曲线的图象得其几何性质;
(2)求双曲线标准方程应先定型,再 定量.
心.双曲线的对称中心叫做双曲线的中心.(-x,-y)(-x,y)(x,y)(x,-y)昭通实验中学 罗跃程3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点探究昭通实验中学 罗跃程a4、渐近线MNP(2)实轴和虚轴等长的双曲线叫做等轴双曲线.昭通实验中学 罗跃程5、离心率e反映了双曲线开口大小
e越大 双曲线开口越大
e越小 双曲线开口越小(3)离心率范围:(2)离心率的几何意义:e>1ab 昭通实验中学 罗跃程(1)范围:(2)对称性:关于x轴、y轴、原点都对称(3)顶点:(0,-a)、(0,a)(4)渐近线:(5)离心率:昭通实验中学 罗跃程例1 :求双曲线的实轴长、虚轴长、焦点坐标、顶点坐标、离心率、渐近线方程。解:由题意可得 实半轴长:虚轴长:焦点坐标:离心率:渐近线方程:例题选讲a=2顶点坐标:(-2,0),(2,0)请你写出一个以 为渐近线的双曲线方程. 你能写出所有以 为渐近线的
双曲线方程吗?相关练习昭通实验中学 罗跃程1、“共渐近线”的双曲线λ>0表示焦点在x轴上的双曲线;λ<0表示焦点在y轴上的双曲线。2、“共焦点”的双曲线(1)与椭圆 有共同焦点的双曲线方程表
示为(2)与双曲线 有共同焦点的双曲线方
程表示为昭通实验中学 罗跃程练习:3、求以椭圆 的焦点为顶点,以椭圆的
顶点为焦点的双曲线的方程。昭通实验中学 罗跃程例4、双曲线型冷却塔的外形,是双曲线
的一部分绕其虚轴旋转所成的曲面,它的
最小半径为12m,上口半径为13m,下口半径
为25m,高55m.选择适当的坐标系,求出此
双曲线的方程(精确到1m). A′A0xC′CB′By例题讲解 昭通实验中学 罗跃程例5、点M(x,y)与定点F(5,0),的距离
和它到定直线 : 的距离的比是常
数 , 求点M的轨迹. y0d昭通实验中学 罗跃程昭通实验中学 罗跃程直线与双曲线问题:例6、如图,过双曲线 的右焦点
倾斜角为 的直线交双曲线于A,B两点,求|AB|。昭通实验中学 罗跃程43(0, -5) 、(0, 5)昭通实验中学 罗跃程2.双曲线的一条渐近线方程为 , 且过点 P (3, ), 则它的标准方程
是 . 昭通实验中学 罗跃程昭通实验中学 罗跃程问:若将题目中“焦点在y轴上”改为“焦点在坐标轴上”呢?先定型,再定量昭通实验中学 罗跃程课堂小结:
通过本节课的学习,你有哪些收获?ab(1)由双曲线的图象得其几何性质;
(2)求双曲线标准方程应先定型,再 定量.
