《正多边形和圆》复习讲义

《正多边形和圆》复习讲义
【知识点1】正多边形及有关概念
（1） 正多边形的定义
（2） 正多边形的中心
（3） 正多边形的中心角
（4） 正多边形的半径
（5） 正多边形的边心距
【例1】如图，已知⊙O是正方形ABCD的外接圆，且⊙O的半径为R，求正方形ABCD的边长、边心距、面积.
【例2】一个长方体的香烟盒，装满大小均匀的20支香烟，打开香烟盒的顶盖后，20支香烟排成三行，如下图所示，经测量一支香烟的直径为0.75cm，长约8.4cm.
（1） 试计算香烟盒顶盖ABCD的面积；（计算结果不取近似值）
（2） 制作这样一个烟盒至少需要多少面积的纸张？（不计算重叠粘合部分，计算结果精确到0.1cm2，）
【练习1】已知：如图，△ABC是⊙O的内接等腰三角形，顶角∠BAC=36°，弦BD、CF分别平分∠ABC、∠ACB.
求证：五边形AEBCD是正五边形.
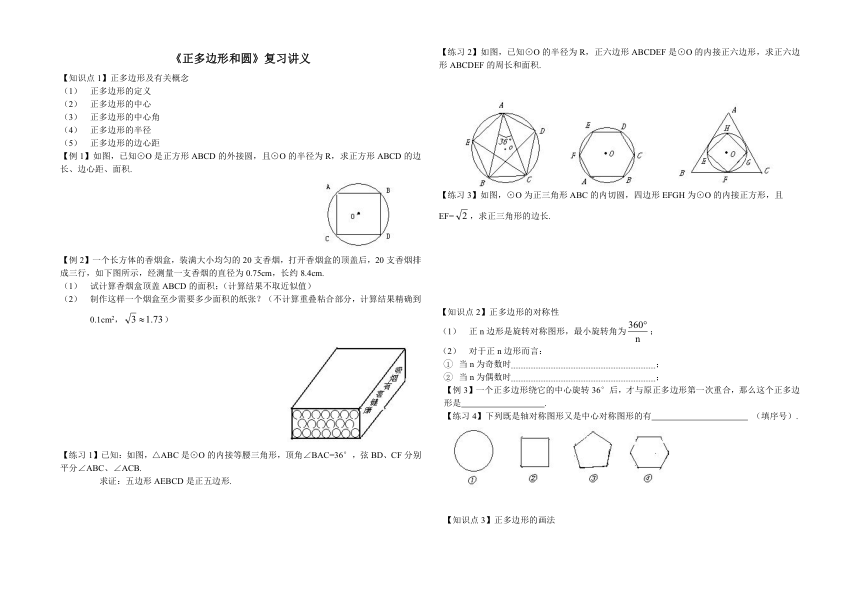
【练习2】如图，已知⊙O的半径为R，正六边形ABCDEF是⊙O的内接正六边形，求正六边形ABCDEF的周长和面积.
【练习3】如图，⊙O为正三角形ABC的内切圆，四边形EFGH为⊙O的内接正方形，且
EF=，求正三角形的边长.
【知识点2】正多边形的对称性
（1） 正n边形是旋转对称图形，最小旋转角为；
（2） 对于正n边形而言：
1 当n为奇数时 ；
2 当n为偶数时 ；
【例3】一个正多边形绕它的中心旋转36°后，才与原正多边形第一次重合，那么这个正多边形是 .
【练习4】下列既是轴对称图形又是中心对称图形的有 （填序号）.
【知识点3】正多边形的画法
（1） 用量角器
（2） 尺规作图
【知识点4】正多边形的有关计算
【例4】已知正六边形ABCDEF内接于⊙O，图中阴影部分面积是，求⊙O的半径.
【例5】如果一个正六边形的面积与一个正三角形的面积相等，求正六边形与正三角形的内切圆的半径之比.
【练习5】如图，圆内接正五边形ABCDE，对角线AC与BD相交于点P，求∠APB.
【练习6】如图，已知⊙O的外切正六边形的半径为4，求该圆的内接正三角形的边心距.
【知识点5】正多边形规律性问题的综合应用
【例3】如图，点M、N分别是⊙O的内接正三角形ABC，内接正方形ABCD，内接正五边形ABCDE，…，内接正n边形的边AB、BC上的点，且BM=CN，连接OM、ON.
（1） 求图1中的∠MON的度数；
（2） 在图2中，∠MON的读数为 ，在图2中，∠MON的读数为 ，
（3） 试探索∠MON的度数与正n边形的边数n之间的关系.（直接写出答案）
【练习7】如图，E、D分别是正三角形ABC，正方形ABCM，正五边形ABCMN中以C为顶点的相邻两边上的点，且BE=CD，DB交AE于点P.
（1） 求图1中∠APD的度数；
（2） 在图2中，∠APD的度数为 ，在图3中∠APD的度数为 ；
（3） 根据前面的探索，你能否将本题推广到一般正n边形情况，若能，请写出推广后的结论，若不能请说明理由.
（4）