1.1建立反比例函数模型
图片预览






文档简介
课件18张PPT。1.1建立反比例函数模型
湖南省新邵县酿溪中学王军旗 1.理解反比例函数的概念,能写出实际问题中成反比关系的函数解析式。 2.培养学生的观察能力以及发现问题、解决问题的能力。 教学目标什么叫一次函数?一般形式是什么?复习提问 如果函数的解析式是关于自变量的一次式,这样的函数就叫一次函数。一般形式是:y=kx+b(k≠0,k,b为常数).新课引言1、谁先到达终点?
甲乙丙丁四人在3000m赛马过程中的
平均速度分别为15m/s,14,5m/s,14.2m/s和
14m/s.那么他们谁先达到终点?设行走的时间为t,则解:设行走的时间为t,则 ,由于分子固定不变,又分母为正数所以当分母越大时,分式的值越小。甲的速度最大,因此用的时间最小,他先到达。 2.坦克为什么要安装宽履带呢?分析:因为压强P与压力F,受力面积s
之间的关系是: ,当压力F一定时,
受力面积S越大,压强P越小。设坦克质
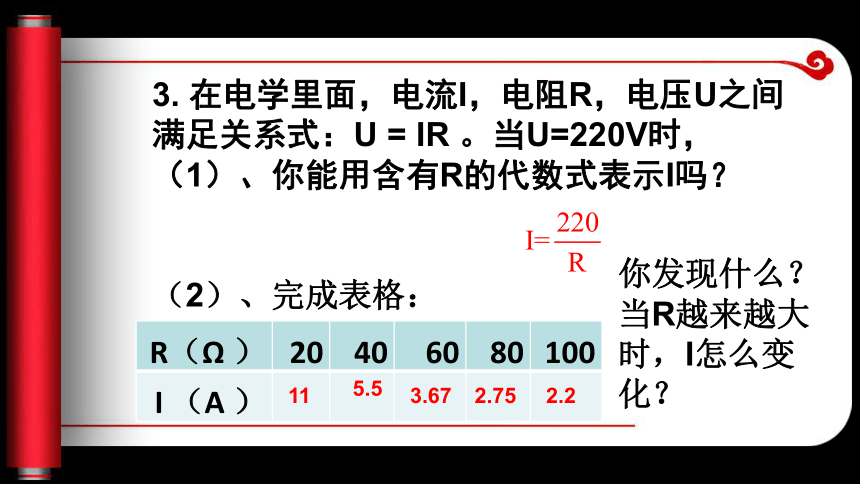
量为40吨,那么 3. 在电学里面,电流I,电阻R,电压U之间满足关系式:U = IR 。当U=220V时, (1)、你能用含有R的代数式表示I吗?(2)、完成表格:115.53.672.752.2你发现什么?当R越来越大时,I怎么变化?上面三个问题的共同特点是:
(1)都有两个变量,
(2)这两个变量的乘积等于一个常数。
一、反比例函数的定义主题讲解思考:上面三个问题具有什么共同特点? 定义:一般地,如果两个变量y与x的关系可 以表示成: 的形式,那么称y是x的反比例函数。 (1)自变量x ≠0 ,函数值y ≠0 ,(2)k为常数,k ≠ 0,如果k的值确定了,那么函数关系也就确定了。(3)函数关系的几种形式:注意!【例1】.下列函数中,x都表示自变量,那么哪些是反比例函数?每一个反比例函数相应的k是多少?
(1) (2)
(3) ,(4)xy=-12
解(1),(2),(4)都是反比例函数,k依次等于5,-0.1,-12
(3)不是反比例函数 若函数 是反比例函数,求出m的值并写出解析式。解:依题意,得:
解得:m=-3.
注意!是反比例函数的条件有两个(1)k ≠0,(2)m=-1变式练习; 【例2】已知y是x的反比例函数,当x=5时,y=10,(1)写出y与x的函数关系。 (2)当x=3时,求y的值。 解(1)∵y是x的反例函数,∴设
∵当x=5时,y=10 ∴
因此:主题二、求反比例函数解析式(2)当x=3时,【例3】.已知,y=y1+y2,y1与x成正比例,y2与x成反比例。且当x=2时,y=-4,当x=-1时,y=5,求出y与x的函数关系。主题三、正反比例函数的综合 【例4】.已知一面积为20的梯形,其上、下底之比为1:3,试写出该梯形的高h和上底a之间的函数关系式,并说明你写的函数是我们学过的什么函数? 解: ,是反比例函数。主题四.反比例函数实际应用1、已知矩形的面积是120cm2,(1)矩形相邻的两条边y(cm)和x(cm)的函数关系是 _____ (2)若y=10cm,则x=____ 变式练习2、在直流电路中,电压u(v)与电流I(A),电阻r(Ω)之间的关系为:U=IR. (1)当电压U=220V时,电流I与电阻R的 关系是____,I是R的_______函数。 (2)当电压U=220时,已知R=10Ω,电流I=____反比例22小结 1、反比例函数的三种形式:2、求反比例函数的解析式只要知道x,y的一组对应值,它们的积就是k的值,k确定了,函数解析式也就确定了。 作业 P4,A1,2,3(本子上),B1,2(做到书上) 3(本子上) 家作:原创(对课题)
湖南省新邵县酿溪中学王军旗 1.理解反比例函数的概念,能写出实际问题中成反比关系的函数解析式。 2.培养学生的观察能力以及发现问题、解决问题的能力。 教学目标什么叫一次函数?一般形式是什么?复习提问 如果函数的解析式是关于自变量的一次式,这样的函数就叫一次函数。一般形式是:y=kx+b(k≠0,k,b为常数).新课引言1、谁先到达终点?
甲乙丙丁四人在3000m赛马过程中的
平均速度分别为15m/s,14,5m/s,14.2m/s和
14m/s.那么他们谁先达到终点?设行走的时间为t,则解:设行走的时间为t,则 ,由于分子固定不变,又分母为正数所以当分母越大时,分式的值越小。甲的速度最大,因此用的时间最小,他先到达。 2.坦克为什么要安装宽履带呢?分析:因为压强P与压力F,受力面积s
之间的关系是: ,当压力F一定时,
受力面积S越大,压强P越小。设坦克质
量为40吨,那么 3. 在电学里面,电流I,电阻R,电压U之间满足关系式:U = IR 。当U=220V时, (1)、你能用含有R的代数式表示I吗?(2)、完成表格:115.53.672.752.2你发现什么?当R越来越大时,I怎么变化?上面三个问题的共同特点是:
(1)都有两个变量,
(2)这两个变量的乘积等于一个常数。
一、反比例函数的定义主题讲解思考:上面三个问题具有什么共同特点? 定义:一般地,如果两个变量y与x的关系可 以表示成: 的形式,那么称y是x的反比例函数。 (1)自变量x ≠0 ,函数值y ≠0 ,(2)k为常数,k ≠ 0,如果k的值确定了,那么函数关系也就确定了。(3)函数关系的几种形式:注意!【例1】.下列函数中,x都表示自变量,那么哪些是反比例函数?每一个反比例函数相应的k是多少?
(1) (2)
(3) ,(4)xy=-12
解(1),(2),(4)都是反比例函数,k依次等于5,-0.1,-12
(3)不是反比例函数 若函数 是反比例函数,求出m的值并写出解析式。解:依题意,得:
解得:m=-3.
注意!是反比例函数的条件有两个(1)k ≠0,(2)m=-1变式练习; 【例2】已知y是x的反比例函数,当x=5时,y=10,(1)写出y与x的函数关系。 (2)当x=3时,求y的值。 解(1)∵y是x的反例函数,∴设
∵当x=5时,y=10 ∴
因此:主题二、求反比例函数解析式(2)当x=3时,【例3】.已知,y=y1+y2,y1与x成正比例,y2与x成反比例。且当x=2时,y=-4,当x=-1时,y=5,求出y与x的函数关系。主题三、正反比例函数的综合 【例4】.已知一面积为20的梯形,其上、下底之比为1:3,试写出该梯形的高h和上底a之间的函数关系式,并说明你写的函数是我们学过的什么函数? 解: ,是反比例函数。主题四.反比例函数实际应用1、已知矩形的面积是120cm2,(1)矩形相邻的两条边y(cm)和x(cm)的函数关系是 _____ (2)若y=10cm,则x=____ 变式练习2、在直流电路中,电压u(v)与电流I(A),电阻r(Ω)之间的关系为:U=IR. (1)当电压U=220V时,电流I与电阻R的 关系是____,I是R的_______函数。 (2)当电压U=220时,已知R=10Ω,电流I=____反比例22小结 1、反比例函数的三种形式:2、求反比例函数的解析式只要知道x,y的一组对应值,它们的积就是k的值,k确定了,函数解析式也就确定了。 作业 P4,A1,2,3(本子上),B1,2(做到书上) 3(本子上) 家作:原创(对课题)
