反比例函数习题课
图片预览





文档简介
课件18张PPT。反比例函数习题课湖南省新邵县酿溪中学王军旗1、什么叫反比例函数?复习提问2、反比例函数的图像有什么特点?(1)图像的两个分支与x、y轴无限接近,但永远不相交。
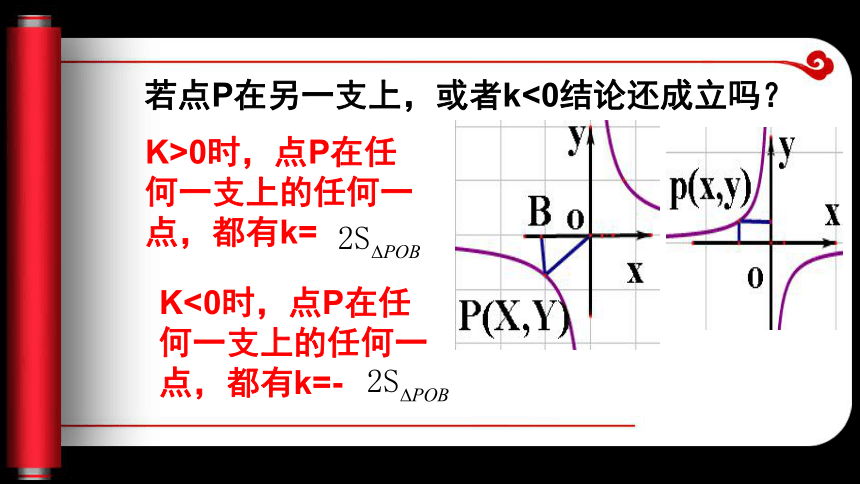
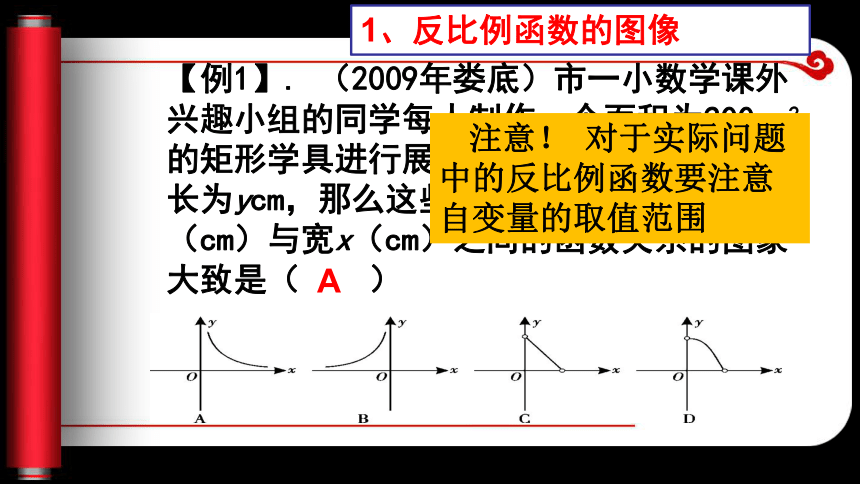
(2) k>0时,图像在第一、三象限,每一支上y随x的增大而减少。(即:小对大,大对小)K<0时,图像在第二、四象限,每一支上,y随x的增大而增大。(即:小对小,大对大)3、如图是反比例函数 的图像,点P(x,y)是图像上一点,PB⊥x轴,垂足为B,则△OPB的面积与k有什么关系? ∵△OPB的面积=?OB·PB=? xy,k=xy, ∴k=2△POB的面积若点P在另一支上,或者k<0结论还成立吗?K>0时,点P在任何一支上的任何一点,都有k=K<0时,点P在任何一支上的任何一点,都有k=-【例1】. (2009年娄底)市一小数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示. 设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( ) 1、反比例函数的图像A 注意! 对于实际问题中的反比例函数要注意自变量的取值范围1(2009年恩施市)一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”图案,如图所示,设小矩形的长和宽分别为 x、y,剪去部分的面积为20,若 2≤x≤10,则 y与x 的函数图象是( )变式练习A 【例2】(2009年鄂州)如图,直线y=mx与双曲 线y= 交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若 =2 ,则k的值是 ( ) A 2, B -2,C m,D 4 2、函数 中k的几何意义。 A1、(2009年常德市)如图1, 已知点C为反比例函数 上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC 的面积为 .变式练习62、(2009年牡丹江市)如图,点 A、B 是 双曲线 上的点,分别经过 A、B 两点向 X轴、 y轴作垂线段,若S阴影=1,则S1+S2= ___4【例3】(2009年重庆)已知:如图,在平面直角坐标系 中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,.tan∠ABO=?,OB=4,OE=2 (1)求该反比例函数的解析式 (2)求直线AB的解析式.3一次函数与反比例函数综合问题【解】:∵tan∠ABO=?,∴OA:OB=1:2, OA=?OB=2, ∴A(0,2),B(4,0) 设直线AB的解析式为y=kx+b, 则 ∴k=-?,b=2 直线AB的解析式 为y=-?x+2. 条件:tan∠ABO=?,OB=4,OE=2 又∵BE=OE+OB=6,CE:BE=1:2, CE=?BE=3, ∴C(-2,3) 设反比例函数的解析式为 , 则k=-2×3=-6 所以反比例函数解析式为:条件:tan∠ABO=?,OB=4,OE=2 (2007四川资阳)如图,已知 A(-4,2)、B(n,-4)是一次函数 y=kx+b的图象与反比例函数 的图象的两个交点. ? (1) 求此反比例函数和一次函数的解析式; (2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.变式练习:【解】 (1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数 的图象上, ∴ 解得 又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上, ∴ 解得 ∴ 反比例函数的解析式为 : 一次函数的解析式为y=-x-2 . 小结:
1反比例函数解析式需要知道自变量和函数的一对值,将这一对值相乘就得到k,函数解析式就确定了。注意实际问题中自变量的取值范围
2、理解k的几何意义时,要注意函数图像在第一、三象限与第二、四想象的区别。
3、要善于从函数图像上获得信息。作业原创P6 18,19 P 8 15
(2) k>0时,图像在第一、三象限,每一支上y随x的增大而减少。(即:小对大,大对小)K<0时,图像在第二、四象限,每一支上,y随x的增大而增大。(即:小对小,大对大)3、如图是反比例函数 的图像,点P(x,y)是图像上一点,PB⊥x轴,垂足为B,则△OPB的面积与k有什么关系? ∵△OPB的面积=?OB·PB=? xy,k=xy, ∴k=2△POB的面积若点P在另一支上,或者k<0结论还成立吗?K>0时,点P在任何一支上的任何一点,都有k=K<0时,点P在任何一支上的任何一点,都有k=-【例1】. (2009年娄底)市一小数学课外兴趣小组的同学每人制作一个面积为200cm2的矩形学具进行展示. 设矩形的宽为xcm,长为ycm,那么这些同学所制作的矩形长y(cm)与宽x(cm)之间的函数关系的图象大致是( ) 1、反比例函数的图像A 注意! 对于实际问题中的反比例函数要注意自变量的取值范围1(2009年恩施市)一张正方形的纸片,剪去两个一样的小矩形得到一个“E ”图案,如图所示,设小矩形的长和宽分别为 x、y,剪去部分的面积为20,若 2≤x≤10,则 y与x 的函数图象是( )变式练习A 【例2】(2009年鄂州)如图,直线y=mx与双曲 线y= 交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若 =2 ,则k的值是 ( ) A 2, B -2,C m,D 4 2、函数 中k的几何意义。 A1、(2009年常德市)如图1, 已知点C为反比例函数 上的一点,过点C向坐标轴引垂线,垂足分别为A、B,那么四边形AOBC 的面积为 .变式练习62、(2009年牡丹江市)如图,点 A、B 是 双曲线 上的点,分别经过 A、B 两点向 X轴、 y轴作垂线段,若S阴影=1,则S1+S2= ___4【例3】(2009年重庆)已知:如图,在平面直角坐标系 中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,.tan∠ABO=?,OB=4,OE=2 (1)求该反比例函数的解析式 (2)求直线AB的解析式.3一次函数与反比例函数综合问题【解】:∵tan∠ABO=?,∴OA:OB=1:2, OA=?OB=2, ∴A(0,2),B(4,0) 设直线AB的解析式为y=kx+b, 则 ∴k=-?,b=2 直线AB的解析式 为y=-?x+2. 条件:tan∠ABO=?,OB=4,OE=2 又∵BE=OE+OB=6,CE:BE=1:2, CE=?BE=3, ∴C(-2,3) 设反比例函数的解析式为 , 则k=-2×3=-6 所以反比例函数解析式为:条件:tan∠ABO=?,OB=4,OE=2 (2007四川资阳)如图,已知 A(-4,2)、B(n,-4)是一次函数 y=kx+b的图象与反比例函数 的图象的两个交点. ? (1) 求此反比例函数和一次函数的解析式; (2) 根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.变式练习:【解】 (1) ∵ 点A(-4,2)和点B(n,-4)都在反比例函数 的图象上, ∴ 解得 又由点A(-4,2)和点B(2,-4)都在一次函数y=kx+b的图象上, ∴ 解得 ∴ 反比例函数的解析式为 : 一次函数的解析式为y=-x-2 . 小结:
1反比例函数解析式需要知道自变量和函数的一对值,将这一对值相乘就得到k,函数解析式就确定了。注意实际问题中自变量的取值范围
2、理解k的几何意义时,要注意函数图像在第一、三象限与第二、四想象的区别。
3、要善于从函数图像上获得信息。作业原创P6 18,19 P 8 15
