12.3.1 等腰三角形
图片预览

文档简介
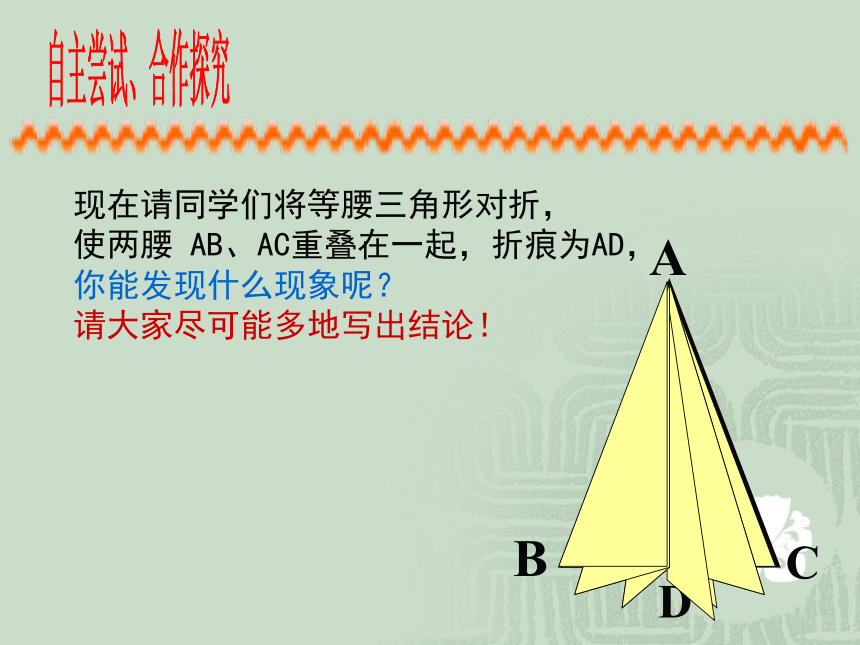
课件12张PPT。阳高五中 曹艳玲12.3.1 等腰三角形自主尝试、合作探究现在请同学们将等腰三角形对折,
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?
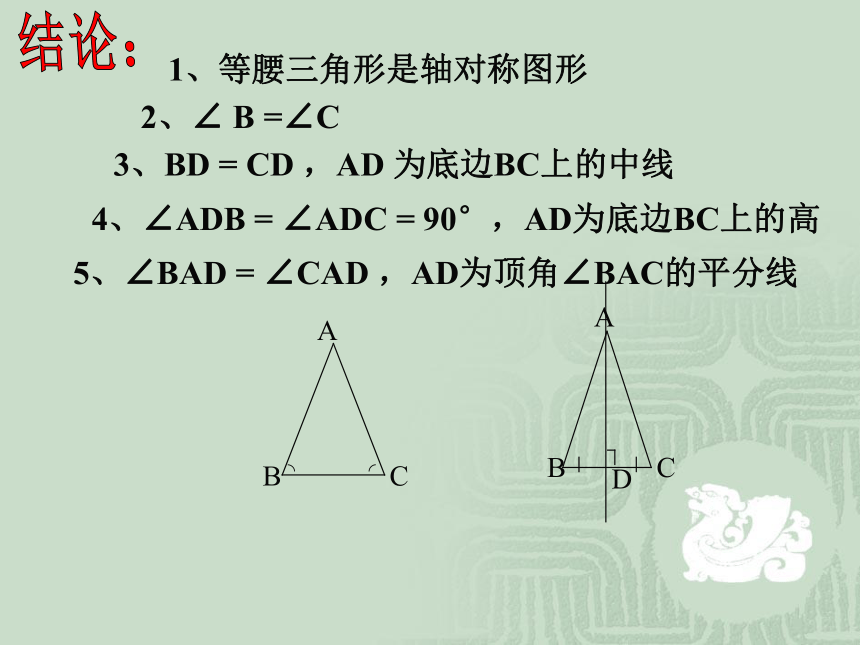
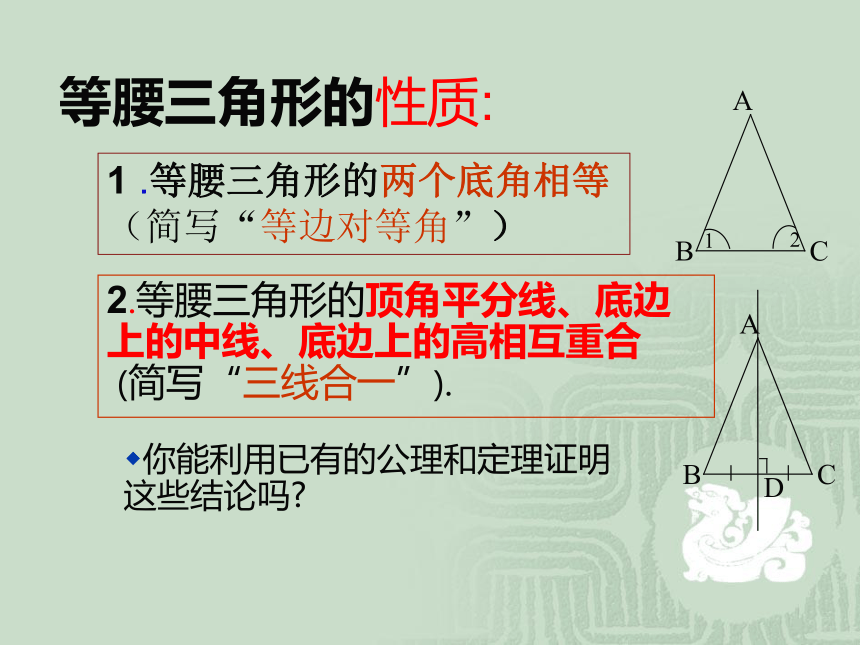
请大家尽可能多地写出结论!结论:1、等腰三角形是轴对称图形2、∠ B =∠C3、BD = CD ,AD 为底边BC上的中线4、∠ADB = ∠ADC = 90°,AD为底边BC上的高5、∠BAD = ∠CAD ,AD为顶角∠BAC的平分线等腰三角形的性质:2.等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
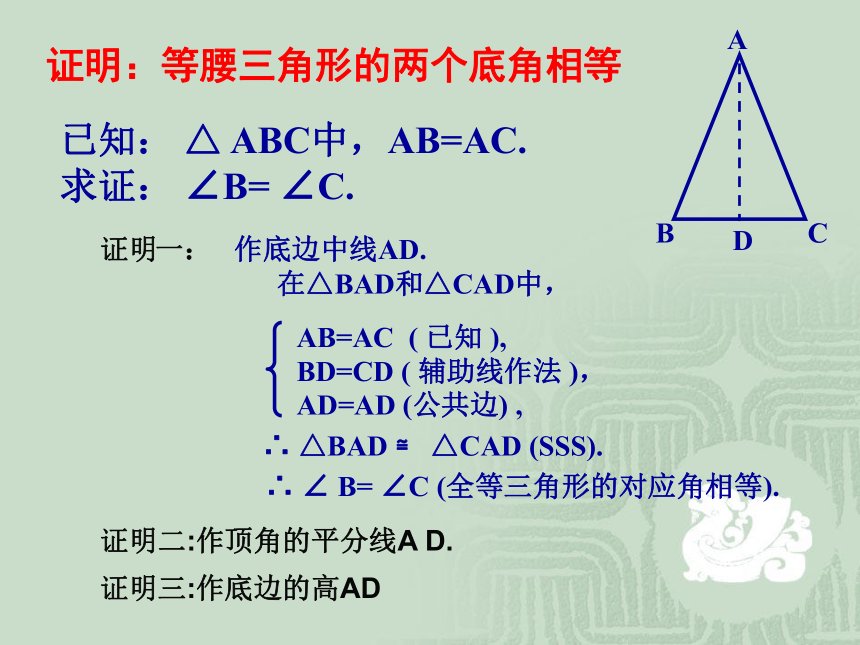
(简写“三线合一”).你能利用已有的公理和定理证明这些结论吗?1 .等腰三角形的两个底角相等 (简写“等边对等角”)证明 一: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等证明二:作顶角的平分线A D.证明三:作底边的高AD等腰三角形的性质1: 等腰三角形的两个底角相等
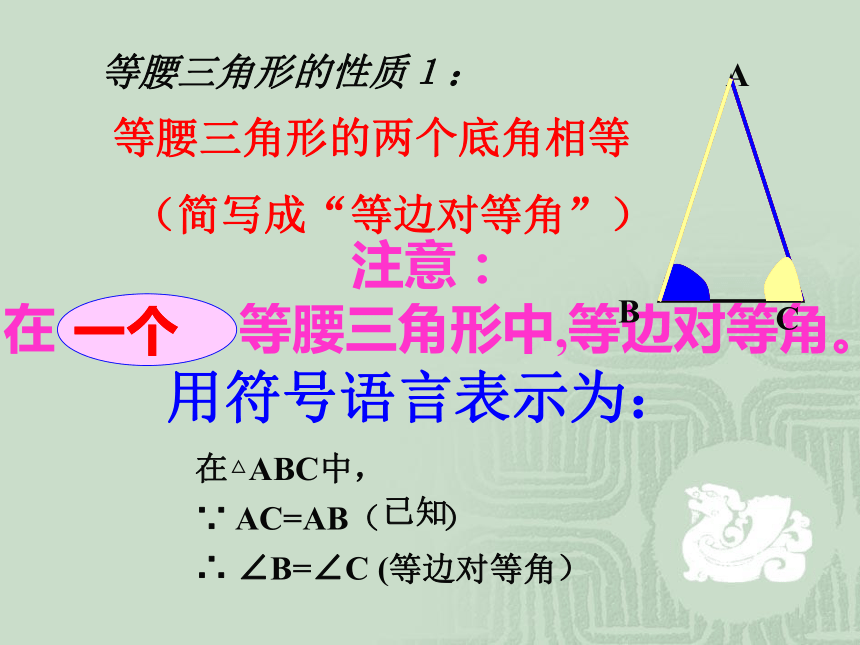
(简写成“等边对等角”)注意:
在 等腰三角形中,等边对等角。用符号语言表示为:在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)设∠A=X,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720问题反馈、精讲典例 75°, 30°70°,40°或55°,55°35°,35°巩固提炼、学情自检4、如图,在△ ABC中,AB=AC,外角∠ ACD=100度,则∠ B=____度
ABCDB80100 °5、如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°, BC=6m,
那么:∠BAC=-----------,BD=-----------120°3m文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结布置作业:课本第51页1、2、3题.
使两腰 AB、AC重叠在一起,折痕为AD,
你能发现什么现象呢?
请大家尽可能多地写出结论!结论:1、等腰三角形是轴对称图形2、∠ B =∠C3、BD = CD ,AD 为底边BC上的中线4、∠ADB = ∠ADC = 90°,AD为底边BC上的高5、∠BAD = ∠CAD ,AD为顶角∠BAC的平分线等腰三角形的性质:2.等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合
(简写“三线合一”).你能利用已有的公理和定理证明这些结论吗?1 .等腰三角形的两个底角相等 (简写“等边对等角”)证明 一: 作底边中线AD.
在△BAD和△CAD中,AB=AC ( 已知 ),BD=CD ( 辅助线作法 ),AD=AD (公共边) ,∴ △BAD ≌ △CAD (SSS).∴ ∠ B= ∠C (全等三角形的对应角相等).已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.D证明:等腰三角形的两个底角相等证明二:作顶角的平分线A D.证明三:作底边的高AD等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 等腰三角形中,等边对等角。用符号语言表示为:在△ABC中,
∵ AC=AB( )
∴ ∠B=∠C ( )已知等边对等角在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD例1 如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角)设∠A=X,则∠BDC=∠A+∠ABD=2X从而∠ABC=∠C=∠BDC=2X于是在△ABC中,有∠A+∠ABC+∠C=X+2X+2X=1800解得 X=360在△ABC中,∠A=360,∠ABC=∠C=720问题反馈、精讲典例 75°, 30°70°,40°或55°,55°35°,35°巩固提炼、学情自检4、如图,在△ ABC中,AB=AC,外角∠ ACD=100度,则∠ B=____度
ABCDB80100 °5、如图,厂房屋顶钢架外框是等腰三角形,
其中AB=AC,,立柱AD⊥BC.已知∠B=30°, BC=6m,
那么:∠BAC=-----------,BD=-----------120°3m文字叙述几何语言等腰三角形的两底角相等(简称等边对等角)∵AB=AC
∴∠B=∠C等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简称三线合一)∵AB=AC,∠1=∠2 ∴AD⊥BC,BD=CD课堂小结布置作业:课本第51页1、2、3题.
