二次方程的实根在区间上的分布

课件15张PPT。二次方程的实根在区间上的分布 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数
y=f(x)的零点。方程f(x)=0有实数根函数零点的定义：等价关系一、复习 如果函数y=f(x)在区间[a,b]上的图象是连续
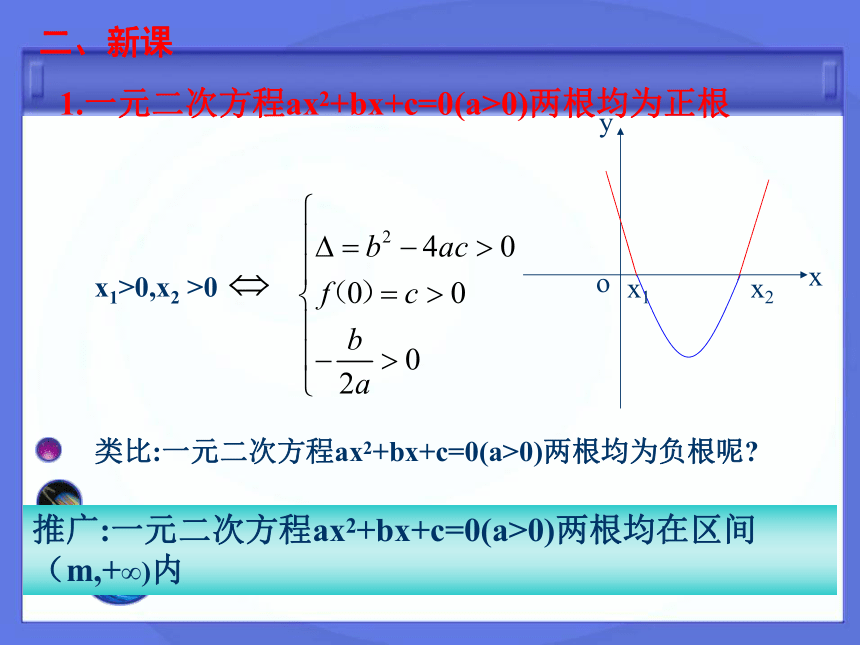
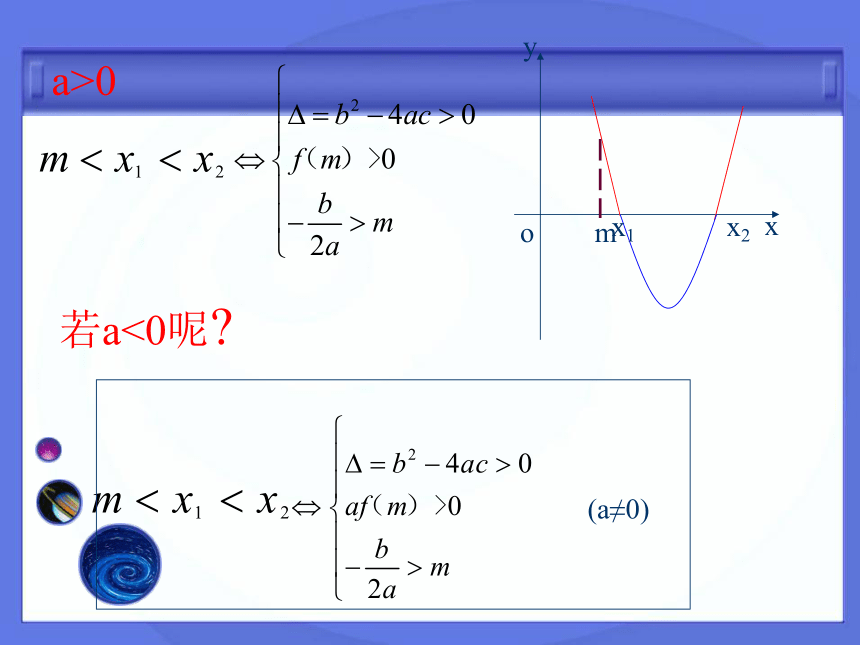
不断的一条曲线，并且有f(a)·f(b)<0，且f(x)在区间（a,b)上为单调函数，那么函数y=f(x)在区间(a,b) 内有且只有一个零点，即存在唯一c∈(a,b)，使得f(c)=0，这个c也就是方程f(x)=0在区间（a,b)上的唯一的实根。零点存在判定法则二次方程ax2+bx+c=0有实数根1.一元二次方程ax2+bx+c=0(a>0)两根均为正根x1>0,x2 >0 类比:一元二次方程ax2+bx+c=0(a>0)两根均为负根呢?推广:一元二次方程ax2+bx+c=0(a>0)两根均在区间（m,+∞)内二、新课x1>0,x2 >0 1.一元二次方程ax2+bx+c=0(a≠0)两根均为正根2.一元二次方程ax2+bx+c=0(a>0)两根均为负根x1<0,x2 <0 a>0若a<0呢?2.一元二次方程ax2+bx+c=0一根为正,另一根为负x1<0求m 的取值范围。 3.如果f（x）=x2+2（m-1）x+2m+6的一个零点大于2，另一个零点小于2,求m 的取值范围。 练一练3.一元二次方程ax2+bx+c=0有且仅有一根在区间（m,n)内则需满足f(m)f(n)<0或1.已知方程x2+（m-2）x+2m-1=0 有且仅有一实根
在（0，1），求m的取值范围。 3.已知方程x2+（m-2）x+2m-1=0 只有较小根在
（0，1），求m的取值范围 2.已知方程x2+（m-2）x+2m-1=0 只有较大根在
（0，1），求m的取值范围。 变3.已知方程x2+（m-2）x+2m-1=0 有根在（0，1），
求m的取值范围 练一练3.一元二次方程ax2+bx+c=0两根分别在区间（k1，k2）以及（p1，p2）之间若是a<0,请同学们画出图形,写出它的等价式?
若方程x2+（a+2）x-a=0 的两实根均在区间（-1，1），求实数a的取值范围。
4.一元二次方程ax2+bx+c=0两根都在区间（m，n）内例已知a是实数，函数f(x)=2ax2+2x-3-a,
如果y=f(x)在区间[-1,1]上有零点，求a的取值范围。综合提高