4.5 三角形的内切圆学案

4、5三角形的内切圆
【知识链接】
1、确定圆的条件有哪些？
2、什么是角平分线？角平分线有哪些性质？
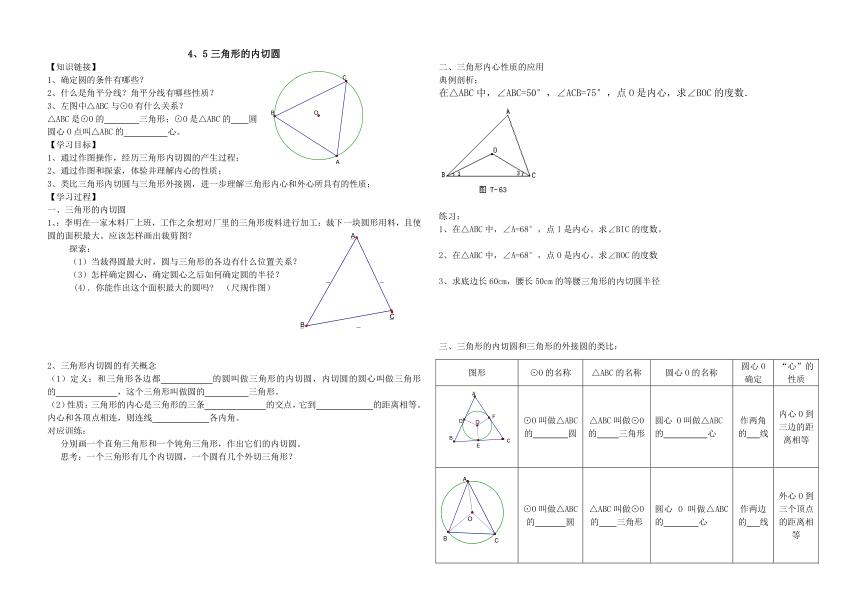
3、左图中△ABC与⊙O有什么关系？
△ABC是⊙O的 三角形；⊙O是△ABC的 圆
圆心O点叫△ABC的 心。
【学习目标】
1、通过作图操作，经历三角形内切圆的产生过程；
2、通过作图和探索，体验并理解内心的性质；
3、类比三角形内切圆与三角形外接圆，进一步理解三角形内心和外心所具有的性质；
【学习过程】
一、三角形的内切圆
1、：李明在一家木料厂上班，工作之余想对厂里的三角形废料进行加工：裁下一块圆形用料，且使圆的面积最大。应该怎样画出裁剪图？
探索：
（1）当裁得圆最大时，圆与三角形的各边有什么位置关系？
（3）怎样确定圆心，确定圆心之后如何确定圆的半径？
(4)．你能作出这个面积最大的圆吗 （尺规作图）
2、三角形内切圆的有关概念
（1）定义：和三角形各边都 的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的 ，这个三角形叫做圆的 三角形。
（2）性质：三角形的内心是三角形的三条 的交点，它到 的距离相等。
内心和各顶点相连，则连线 各内角。
对应训练：
分别画一个直角三角形和一个钝角三角形，作出它们的内切圆。
思考：一个三角形有几个内切圆，一个圆有几个外切三角形？
二、三角形内心性质的应用
典例剖析；
在△ABC中，∠ABC=50°，∠ACB=75°，点O是内心，求∠BOC的度数．
练习：
1、在△ABC中，∠A=68°，点I是内心。求∠BIC的度数。
2、在△ABC中，∠A=68°，点O是内心。求∠BOC的度数
3、求底边长60cm，腰长50cm的等腰三角形的内切圆半径
三、三角形的内切圆和三角形的外接圆的类比：
图形 ⊙O的名称 △ABC的名称 圆心O的名称 圆心O确定 “心”的性质
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两角的 线 内心O到三边的距离相等
⊙O叫做△ABC的 圆 △ABC叫做⊙O的 三角形 圆心 O叫做△ABC的 心 作两边的 线 外心O到三个顶点的距离相等
四、挑战自我
见课本P131 （你能独立完成吗？）
练习：△ABC中，∠C=90°，BC=3,AC=4,求这个三角形的内切圆的半径。
【归纳小结】本节课你学到了什么？说说看。
【课堂检测】
1.给出下列命题：①任一个三角形一定有一个外接圆，并且只有一个外接圆；②任一个圆一定有一个内接三角形，并且只有一个内接三角形；③任一个三角形一定有一个内切圆，并且只有一个内切圆；④任一个圆一定有一个外切三角形，并且只有一个外切三角形．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
2. 正三角形内切圆半径r与外接圆半径R之间的关系为（ ）
A．4R=5r B．3R=4r C．2R=3r D．R=2r
3.如图，⊙O内切于，切点分别为．已知， ，连结 HYPERLINK "http://www.1230.org" EMBED Equation.DSMT4 ，那么等于（ ）
A. B. C. D.
【作业布置】
1、 延伸性作业：
如图，点I是△ABC的内心，线段AI的延长线交△ ABC的外接圆于点D，交BC边于点E．求证：ID=BD.
2、预习性作业：自学课本P133、P134内容。知道两不等圆由远及近有怎样的位置关系？不同的位置关系有什么性质，又是如何判断的？
。
_
_
E
_
B
C
_
A
_
B
_
C
F
A
O
D