第九章 角 单元能力考查

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
七下第9章测试 总第 课时
角 单元能力考查
一、填空题（每小题3分，共36分）：
1、上午9点整，钟面上的时针与分针的夹角是 度。
2、125.23 = （用度、分、秒表示）。
3、∠1的补角是133 21′，则它的余角是
4、已知：OC平分∠AOB，则 = = 。
5、如果∠1与∠2互为补角，∠1=72 ,∠2=_____ ,若∠3=∠1，则∠3的补角为_______ ，理由是__________________________。
6、如右图，一长方形纸条ABCD沿直线EF折叠，
点C、D分别落到点M、N，且∠FEG＝61○，则∠1＝_____度。
7、0.5周角= 平角= 直角= 度。
8、若∠1：∠2：∠3=1：2：3，且∠1+∠2+∠3=180°，
则∠2= 度。
9、如图，，则＝ ，
如果，那么＝ 。
10、如图，由点O引射线OA，OB，OC，则这三条射线形成____个角，
其中用数字表示是_ ___，用三个字母表示
是___ _。
11、如图，，是的平分线，
是的平分线，则的度数是。
12、如图2-116中的40°角应写成__ ____方向，70°角应写成__ ____方向。
二、选择题（每小题3分，共30分）：
1、在下面四个图形中，能用三种方法表示同一个角的图形是（ ）
A B C D
2、已知∠AOB=30°，∠BOC=80°，∠AOC=50°，那么（ ）
A、 射线OB在∠AOC内；射线OB在∠AOC外；
B、 射线OB与射线OA重合；射线OB与射线OC重合。
C、 以上都有可能
D、 以上都不对
3、如图所示，∠1=15°，∠AOC=90°，点B、O、D在同一直线上，则∠2的度数为（ ）
A、75°；B、15°；C、105°；D、165°
4、两个锐角的和（ ）
A.一定是锐角；B.一定是直角；C.一定是钝角；D.可能是钝角、直角或钝角。
5、下列计算错误的是( )
A、0.25°=900″；B、(1)°=90′；C、1000″=()°；D、125.45°=125°45′
6、已知：∠AOC＝x，OA⊥OB，OD⊥OC，那么∠BOD的度数是( )
A、180°－x；B、90°－x；C、90°＋x；D、2x一90°
7、如右图，已知∠AOC=∠BOD=90 ，∠AOD=150 ，则∠BOC的度数为（ ）
A、30 ；B、45 ；C、50 ；D、60
8、下列说法正确的有（ ）
（1）互补的两个角中，至少有一个角大于或等于直角；（2）一个角的补角必是钝角；（3）两个锐角一定互为余角；（4）直角没有补角；（5）如果∠MON=180 ,那么M、O、N三点在一条直线上；（6）一个角的补角一定比这个角大。
A、1个；B、2个；C、3个；D、4个。
9、下列语句正确的是（ ）
A、平角就是一条直线；B、周角就是一条射线；C、小于平角的角是钝角；D、一周角等于四个直角。
10、若点B在点A的北偏东30度，则点A在点B的（ ）
A、南偏西30度；B、北偏东60度；C、南偏西60度；D、西偏南60度。
注意：请将选择题答案序号填写在下表中：
题号 1 2 3 4 5 6 7 8 9 10
答案
三、计算（每题6分，共24分）：
1、（1）180 -（34 55′+21 33′）；（2）(180°－91°32′24″)2
2、已知一个角的补角比这个角的余角的2倍多15度，求这个角。
3、如图，OE为∠AOD的平分线，∠COD=∠EOC，
∠COD=15°，求：①∠EOC的大小；②∠AOD的大小。
4、已知。求：的度数。
四、探索与实践：
1、（6分）画∠AOB=60 ；在OA、OB边上分别截取
OE=2.5cm,OF=3.5cm，并连结EF；画∠AOB的平分线交EF于C。
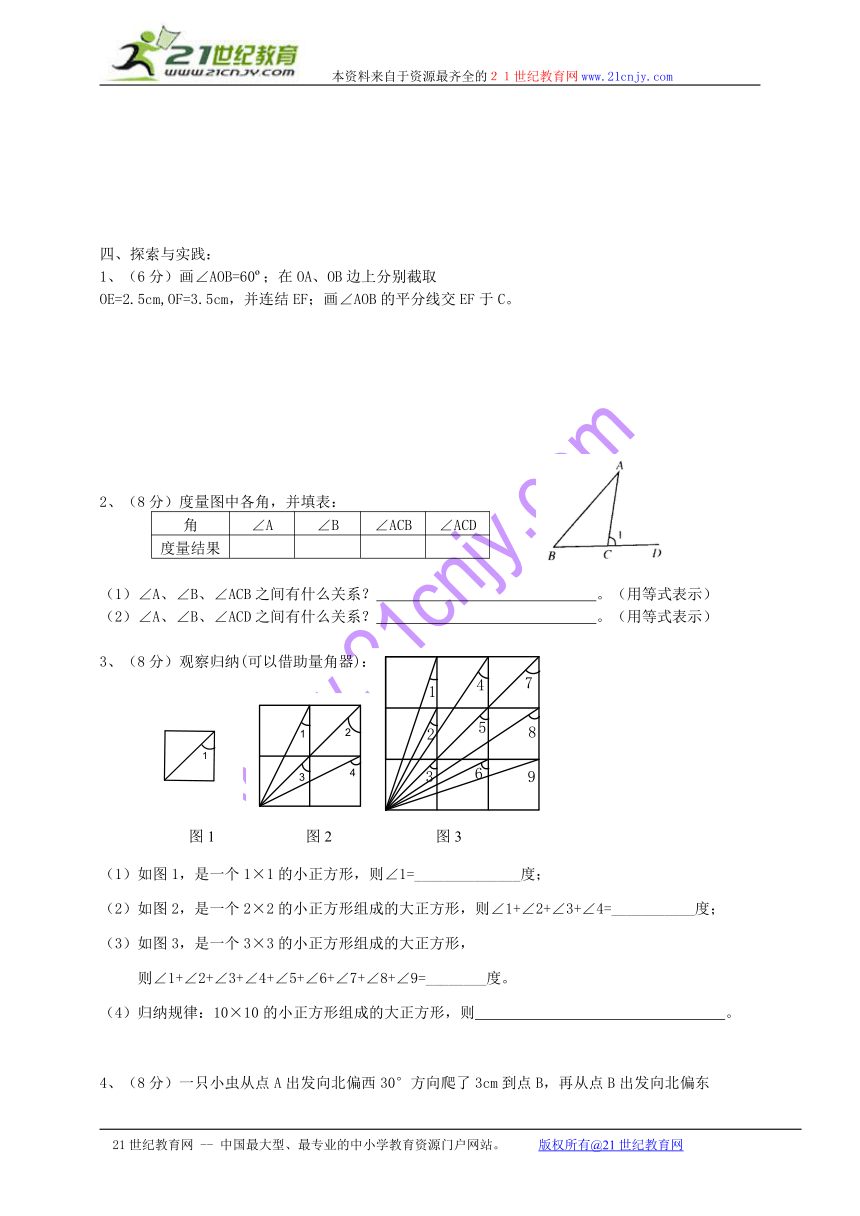
2、（8分）度量图中各角，并填表：
角 ∠A ∠B ∠ACB ∠ACD
度量结果
（1）∠A、∠B、∠ACB之间有什么关系？ 。（用等式表示）
（2）∠A、∠B、∠ACD之间有什么关系？ 。（用等式表示）
3、（8分）观察归纳(可以借助量角器)：
（1）如图1，是一个1×1的小正方形，则∠1=______________度；
（2）如图2，是一个2×2的小正方形组成的大正方形，则∠1+∠2+∠3+∠4=___________度；
（3）如图3，是一个3×3的小正方形组成的大正方形，
则∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8+∠9=________度。
（4）归纳规律：10×10的小正方形组成的大正方形，则 。
4、（8分）一只小虫从点A出发向北偏西30°方向爬了3cm到点B，再从点B出发向北偏东
60°爬了3cm到点C。
（1）试画图确定A、B、C的位置；
（2）从图上量出点C到点A的距离（精确到0.1cm）；
（3）指出点C在点A的什么方位
10.1 同位角
教师寄语 求学将以致用； 读书贵在虚心。
学习目标 1、经历从现实生活中抽象出相交线和角的过程。
2、以两条直线相交所形成的四个角为知识基础，进一步研究两条直线被第三条直线所截成八个角，能根据图形特征识别同位角、内错角和同旁内角。
预习要求（做好准备，迎接挑战）
1. 预习教材P26-P27 的内容。
2. 能根据图形特征识别同位角、内错角和同旁内角。E
学习过程 A 2 1 B
自主探究 合作交流（八仙过海，各显神通） 6 5 D
任务一：同位角、内错角和同旁内角的定义 C 7 8 F
1、直线AB与CD被直线EF所截，共形成 个角。
2、观察∠1与∠5，它们的位置有什么关系？
我们把∠1与∠5具有这种位置关系的一对角叫 。图中还有这样的角吗？
3、观察∠3与∠5，它们的位置有什么关系？
我们把∠3与∠5具有这种位置关系的一对角叫 。图中还有这样的角吗？
4、观察∠3与∠6，它们的位置有什么关系？
我们把∠3与∠6具有这种位置关系的一对角叫 。图中还有这样的角吗？
总结：当两条直线被第三条直线所截时，如何识别同位角、内错角和同旁内角？
任务二：同位角、内错角和同旁内角的应用
1、 图中，直线EF与GH被直线AB所截，哪些是同位角？F H
哪些是内错角？哪些是同旁内角？ A C D B
解：
E G
2、在图中，直线a,b被直线l所截。（1）就位置关系而言，∠1与∠5是什么角？
（2）如果∠1=∠5，那么在标出的角中与∠1相等的角有哪些？与∠1互补的角有哪些？ a b
l
当堂测试（奋力拼搏，冲刺目标）
1、观察图（1）并填空：（1）∠1与______是同位角 （2）∠5与_______是同旁内角 （3）∠2与_______是内错角
2、如图 (2)
（1）∠1的同位角是_______ (2) ∠1 的内错角是________
(3) ∠2与∠5是___________
3、如图(3),直线a.b被c所截
（1）写出所有的同位角________________ 内错角________________
同旁内角______________
（2）若∠3＝∠5，那么与∠5相等的还有_____________.
与∠5互补的角有_________________.
学习小结：
1.我掌握的知识：
2. 我不明白的问题：
C
D
B
A
O
C D
E
O A
图2
图1
图3
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网