积的乘方和幂的乘方
图片预览

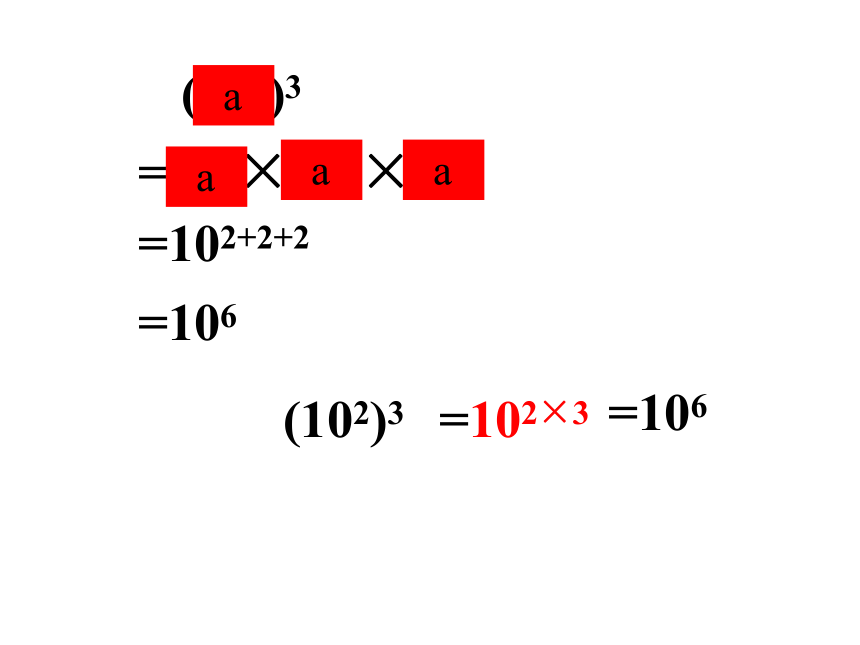


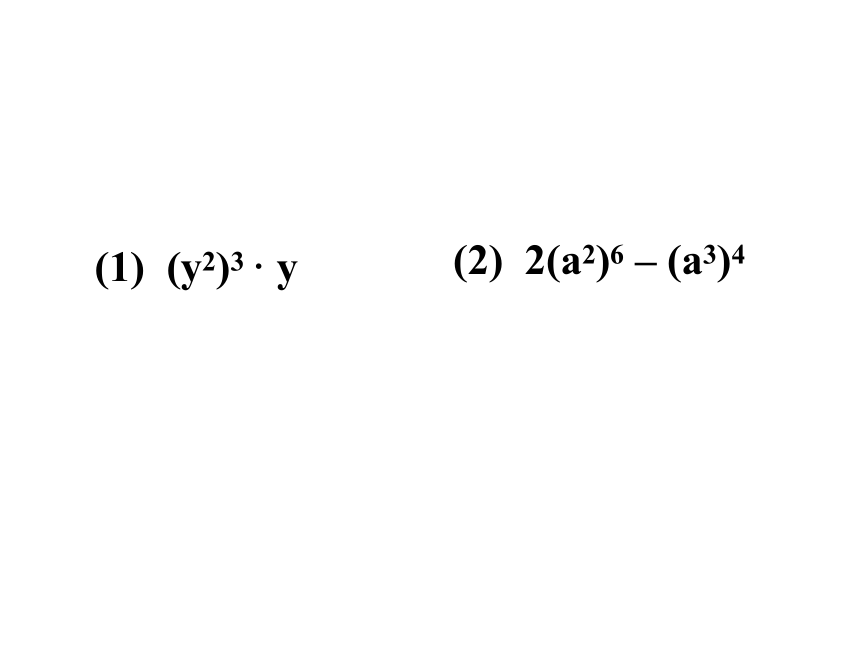




文档简介
课件21张PPT。复习幂的意义:an =同底数幂乘法的运算法则:
底数不变,指数相加。am · an=am+n(m,n都是正整数)(102)3=102×102×102=102+2+2=102×3=106 a a a a(102)3=106例1 计算:
(104)3 ; (2) (b5)5 ; (3) (an)3;
(4) -(x2)m ;
(1) (104)3解:(2) (b5)5(3) (an)3(4) -(x2)m(4) (am)n=amn(am)n=amn (m,n都是正整数).底数 ,
指数 . 不变相乘幂的乘方:(1) (y2)3 · y(2) 2(a2)6 – (a3)4练一练计算:
(103)3 ; (2) –(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2 ;
(6) x·x4 – x2 · x3 .2. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 . 2、计算:
(2×3)2与22 × 32,你会发现什么?填空:3、观察、猜想:
(ab)3与a3b3 是什么关系呢?(ab)3= 猜想:(ab)n=anbn (n为正整数) =anbn证明:思考:(ab)n =?积的乘方语言叙述: 积的乘方等于把积的每个因式分别乘方,再把所得的幂相乘。 推广:三个或三个以上的积的乘方等于什么?(abc)n = anbncn (n为正整数)(ab)n = anbn (n为正整数)例1:计算:
(1) (-3x)3 (2) (-5ab)2
(3) (xy2)2 (4) (-2xy3z2)4 下列各式对吗?请说出你的观点和理由:
(1) ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) ( ) 已知,44?83=2x,求x的值. 实践与创新1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xm能力提升2、 9m·27n可以写为: ( )
A. 9m+3n B. 27m+n
C. 32m+3n D. 33m+2n
1 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10;
(2)a2m =( )2 =( )m (m为正整数).
20x4x5 x2 ama2幂的乘方法则的逆用实践与创新1、若am=2,an=3,求① am+n 的值。② a3m+2n的值。2、若9×27x = 34x+1,求x的值.逆用公式三、巩固练习 2、若(x2)n=x8,则n=_______ 3、若[(x3)m]2=x12,则m=_______ 4、若xm?x2m=2,求x9m的值.说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2小结:
1、本节课的主要内容: 幂的运算的三个性质:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都为正整数)积的乘方2、如果单项式 -3x2ay3 与 2x4y3b-3 的和仍为单项式,试求它们的积。
底数不变,指数相加。am · an=am+n(m,n都是正整数)(102)3=102×102×102=102+2+2=102×3=106 a a a a(102)3=106例1 计算:
(104)3 ; (2) (b5)5 ; (3) (an)3;
(4) -(x2)m ;
(1) (104)3解:(2) (b5)5(3) (an)3(4) -(x2)m(4) (am)n=amn(am)n=amn (m,n都是正整数).底数 ,
指数 . 不变相乘幂的乘方:(1) (y2)3 · y(2) 2(a2)6 – (a3)4练一练计算:
(103)3 ; (2) –(a2)5 ; (3) (x3)4 · x2 ;
(4) [(-x)2 ]3 ; (5) (-a)2(a2)2 ;
(6) x·x4 – x2 · x3 .2. 判断下面计算是否正确?如果有错误请改正:
(1) (x3)3 = x6 ; (2)a6 · a4 = a24 . 2、计算:
(2×3)2与22 × 32,你会发现什么?填空:3、观察、猜想:
(ab)3与a3b3 是什么关系呢?(ab)3= 猜想:(ab)n=anbn (n为正整数) =anbn证明:思考:(ab)n =?积的乘方语言叙述: 积的乘方等于把积的每个因式分别乘方,再把所得的幂相乘。 推广:三个或三个以上的积的乘方等于什么?(abc)n = anbncn (n为正整数)(ab)n = anbn (n为正整数)例1:计算:
(1) (-3x)3 (2) (-5ab)2
(3) (xy2)2 (4) (-2xy3z2)4 下列各式对吗?请说出你的观点和理由:
(1) ( )
(2) a4 a3=a12 ( )
(3) (a2)3+(a3)2=(a6)2 ( )
(4) (-x3)2=(-x2)3 ( )
(5) ( ) 已知,44?83=2x,求x的值. 实践与创新1.下列各式中,与x5m+1相等的是( )
(A)(x5)m+1 (B)(xm+1)5
(C) x · (x5)m (D) x · x5 · xm能力提升2、 9m·27n可以写为: ( )
A. 9m+3n B. 27m+n
C. 32m+3n D. 33m+2n
1 计算:
2(x3)2 · x3-(3x3)3+(5x)2 ·x7幂的乘方的逆运算:
(1)x13·x7=x( )=( )5=( )4=( )10;
(2)a2m =( )2 =( )m (m为正整数).
20x4x5 x2 ama2幂的乘方法则的逆用实践与创新1、若am=2,an=3,求① am+n 的值。② a3m+2n的值。2、若9×27x = 34x+1,求x的值.逆用公式三、巩固练习 2、若(x2)n=x8,则n=_______ 3、若[(x3)m]2=x12,则m=_______ 4、若xm?x2m=2,求x9m的值.说明:逆用积的乘方法则 anbn = (ab)n可以解一些复杂的计算。解法二: (0.04)2004×[(-5)2004]2小结:
1、本节课的主要内容: 幂的运算的三个性质:
am·an=am+n (am)n=amn
(ab)n=anbn ( m、n都为正整数)积的乘方2、如果单项式 -3x2ay3 与 2x4y3b-3 的和仍为单项式,试求它们的积。
