椭圆的标准方程

课件25张PPT。椭圆及其标准方程如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢？生活中的椭圆一.课题引入：椭圆的形成过程行星运行的轨道我们的太阳系二.讲授新课：平面内到两个定点F1、F2的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点，1 .椭圆定义：注意:椭圆定义中容易遗漏的四处地方：
（1） 必须在平面内;（2）两个定点---两点间距离确定;（3）定长---轨迹上任意点到两定点距离和确定.两焦点间的距离叫做椭圆的焦距（一般用2c表示）。(4)|MF1|+|MF2|>|F1F2|探究:感悟:(1)若|MF1|+|MF2|>|F1F2|,M点轨迹为椭圆.(1)已知A(-3,0),B(3,0),M点到A,B两点的距离和为10,则M点的轨迹是什么?(2)已知A(-3,0),B(3,0),M点到A,B两点的距
离和为6,则M点的轨迹是什么?(3)已知A(-3,0),B(3,0),M点到A,B两点的距
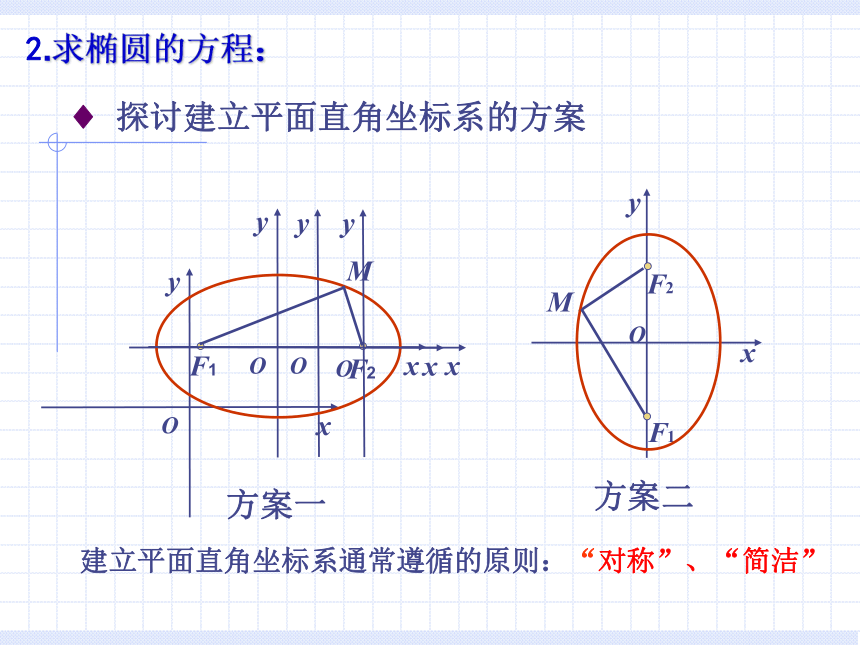
离和为5,则M点的轨迹是什么?椭圆线段AB不存在 (3)若|MF1|+|MF2|<|F1F2|,M点轨迹不存在.(2)若|MF1|+|MF2|=|F1F2|,M点轨迹为线段.建系：设点：列式：化简：证明：建立适当的直角坐标系；设M（x,y）是曲线上任意一点；建立关于x,y的方程 f(x,y)=0；化简方程f(x,y)=0.说明曲线上的点都符合条件，（纯粹性）；符合条件的点都在曲线上（完备性）。2.求椭圆的方程： 复习求曲线方程的方法步骤是什么？(证明一般省略不写,如有特殊情况，可以适当予以说明)? 探讨建立平面直角坐标系的方案建立平面直角坐标系通常遵循的原则：“对称”、“简洁”方案一2.求椭圆的方程：解：取过焦点F1、F2的直线为x轴，线段F1F2的垂直平分线为y轴，建立平面直角坐标系(如图). 设M(x, y)是椭圆上任意一点，椭
圆的焦距2c(c>0)，M与F1和F2的距
离的和等于正常数2a (2a>2c) ，则
F1、F2的坐标分别 是(?c,0)、(c,0) .由椭圆的定义得：代入坐标（问题：下面怎样化简？）由椭圆定义可知两边再平方，得移项，再平方它表示：
① 椭圆的焦点在x轴
② 焦点坐标为F1（-C，0）、F2（C，0）
③ c2= a2 - b2
椭圆的标准方程⑴思考：当椭圆的焦点在y轴上时,它的标准方程是怎样的呢椭圆的标准方程⑵它表示:
① 椭圆的焦点在y轴
② 焦点是F1（0，-c）、 F2（0，c）
③ c2= a2 - b2 总体印象：对称、简洁，“像”直线方程的截距式焦点在y轴：焦点在x轴：3.椭圆的标准方程: 图 形方 程焦 点F(±c，0)F(0，±c)a,b,c之间的关系c2=a2-b2|MF1|+|MF2|=2a (2a>2c>0)定 义共同点：椭圆的标准方程表示的一定是焦点在坐标轴上，中心
在坐标原点的椭圆；方程的左边是平方和，右边是1. 不同点：焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.3.椭圆标准方程的再认识：答：在 X 轴。（-3，0）和（3，0）答：在 y 轴。（0，-5）和（0，5）答：在y 轴。（0，-1）和（0，1）判断椭圆标准方程的焦点在哪个轴上的准则：
焦点在分母大的那个轴上。例1】判定下列椭圆的标准方程在哪个轴上，并写出焦点坐标。 例题精析例2、填空：
已知椭圆的方程为： ，则a=_____，b=_______，c=_______，焦点坐标为：____________焦距等于______;若CD为过左焦点F1的弦，则△F2CD的周长为________543(3,0)、(-3,0)620变式： 若椭圆的方程为 ,试口答完成（1）.1、已知椭圆的方程为： ，则a=_____，b=_______，c=_______，焦点坐标为：___________焦距等于__________;曲线上一点P到焦点F1的距离为3，则点P到另一个焦点F2的距离等于_________，则△F1PF2的周长为___________21(0,-1)、(0,1)2跟踪练习：例3．椭圆的两个焦点的坐标分别是（－4，0）
（4，0），椭圆上一点M到两焦点距离之和等于10，
求椭圆的标准方程。 讲评例题.
解： ∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2－c2=52－42=9
∴所求椭圆的标准方程为
解题感悟：求椭圆标准方程的步骤： ①定位：确定焦点所在的坐标轴；②定量：求a, b的值.例4：若方程4x2+kx2=1表示的曲线是焦点在y轴上的椭圆，求k的取值范围。∵方程表示的曲线是焦点在y轴上的椭圆解之得：0下列条件的m的取值范围：
①表示一个圆；
②表示一个椭圆；
③表示焦点在x轴上的椭圆。探究与互动：2、方程 ，分别求方程满足下列条件的
m的取值范围：
①表示一个圆；
探究与互动：析：方程表示圆需要满足的条件：2、方程 ，分别求方程满足下列条件
的m的取值范围：
①表示一个圆；
②表示一个椭圆；
探究与互动：析：方程表示一个椭圆需要满足的条件：2、方程 ，分别求方程满足
下列条件的m的取值范围：
①表示一个圆；
②表示一个椭圆；
③表示焦点在x轴上的椭圆。探究与互动：析：表示焦点在x轴上的椭圆需要满足的条件：解题感悟：
方程表示椭圆时要看清楚限制条件，焦点在哪个轴上。(2)焦点为F1(0,－3)，F2(0,3),且a=5；(1)a= ,b=1,焦点在x轴上；(3)两个焦点分别是F1(－2,0)、F2(2,0),且过P(2,3)点； 课堂练习：求适合下列条件的椭圆的标准方程：1、椭圆的定义（强调2a>|F1F2|）和椭圆的标
准方程 2、椭圆的标准方程有两种，注意区分 4、求椭圆标准方程的方法 小结3、根据椭圆标准方程判断焦点位置的方法