利用三角形全等测距离

课件14张PPT。利用三角形全等测距离一、复习旧知识1、要证明两个三角形全等应有哪些必要条件？（1）“SSS”：三边对应相等的两个三角形全等.（2）“ASA”：两角和它们的夹边对应相等的两个三角
形全等.（3）“AAS”：两角和其中一角的对边对应相等的两个
三角形全等.（4）“SAS”：两边和它们的夹角对应相等的两个三角
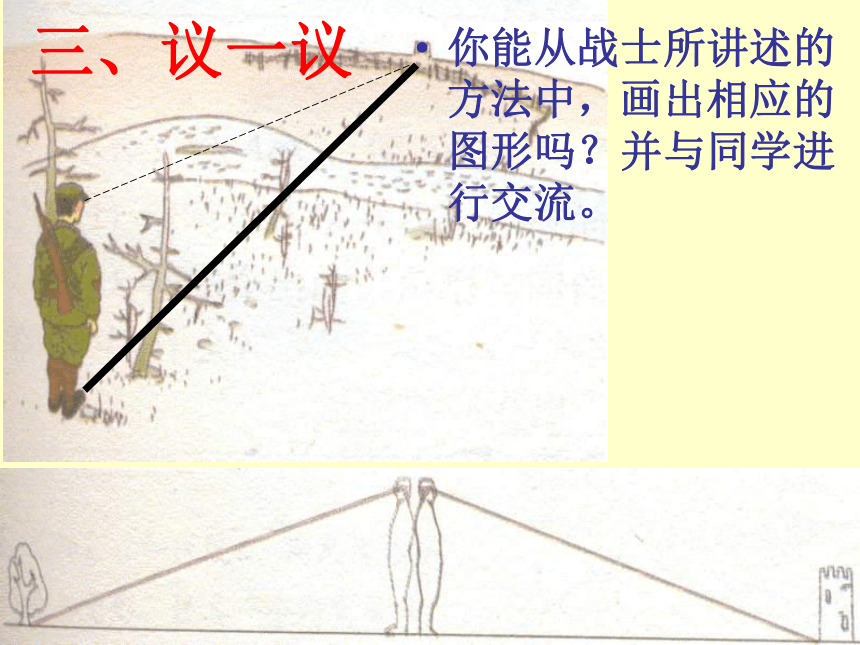
形全等.二、 想一想1.一位经历过战争的老人讲述的故事(见课本P150课文)你能从战士所讲述的方法中，画出相应的图形吗？并与同学进行交流。
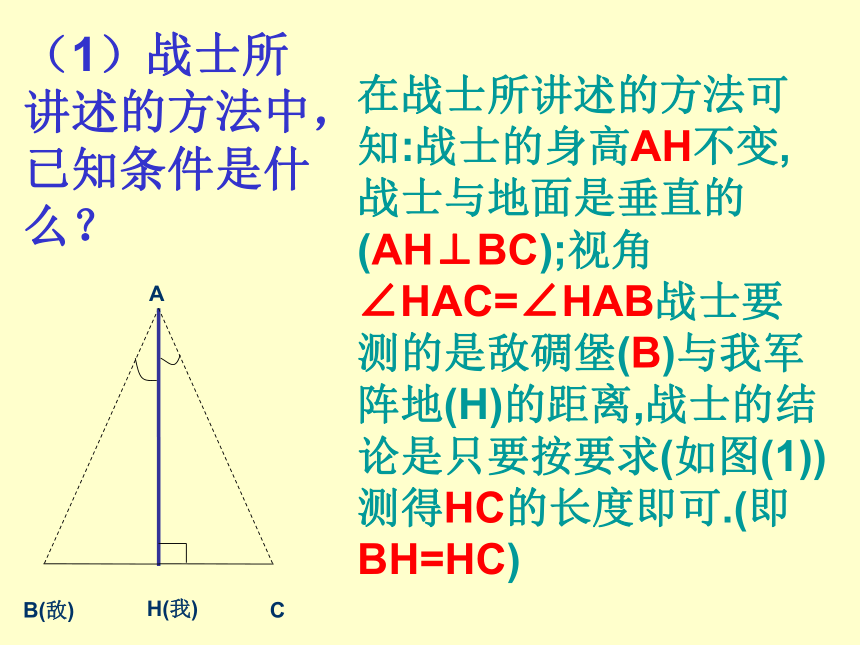
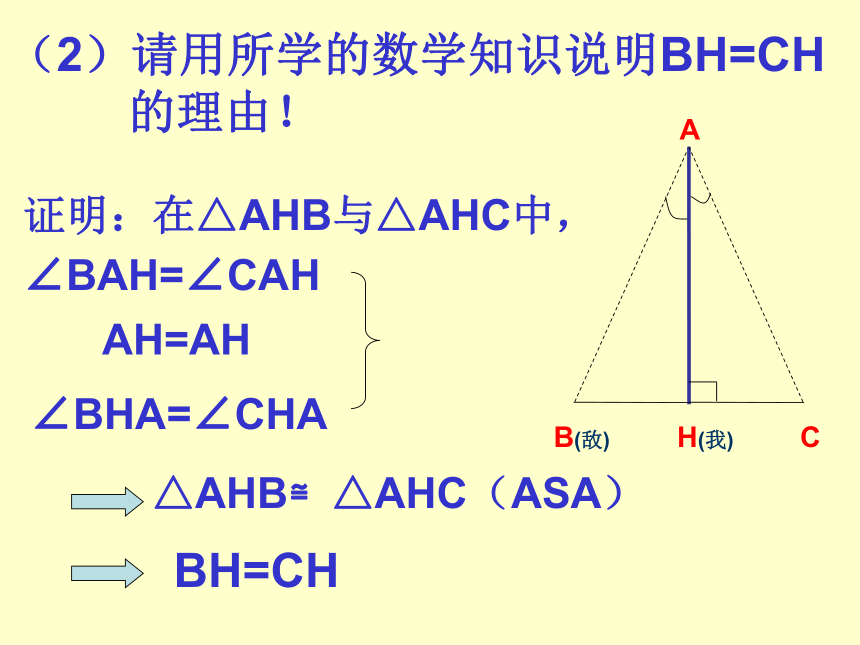
三、议一议在战士所讲述的方法可知:战士的身高AH不变,战士与地面是垂直的(AH⊥BC);视角∠HAC=∠HAB战士要测的是敌碉堡(B)与我军阵地(H)的距离,战士的结论是只要按要求(如图(1))测得HC的长度即可.(即BH=HC)AB(敌)CH(我)（1）战士所讲述的方法中，已知条件是什么？（2）请用所学的数学知识说明BH=CH
的理由！证明：在△AHB与△AHC中，方案1：见课本P-151课文所设计的方案；方案2：方案3：2、已知：A、B两点被一个池塘隔开，无法直接测量，但两点可以到达，请你给出一个合适可行的方案，画出设计图说明依据。先在地上取一个可以直接到达A点和B点的点C，连接AC并延长到D，使CD=AC；连接BC并延长到E，使CE=CB，连接DE并测量出它的长度，DE的长度就是A，B间的距离。方案一返回方
案
二如图，先作三角形ABC,再找一点D，使AD∥BC，并使AD=BC，连结CD，量CD的长即得AB的长返回方案三如图，找一点D，使AD⊥BD，延长AD至C，使CD=AD，连结BC，量BC的长即得AB的长。∴ BA = BC补充练习设计方案：四、师生小结（2）运用所学有关知识设计合适可行的方案，并进行说明理由的过程（1）应用三角形全等测量距离(构造全等三角形)（3）数学知识源于生活实际，而用于实际的重大意义五、作业1、课本P-152[习题5.12] 1、2