5.1.1相交线
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新授课
七年级数学学科(下册)
5.1.1相交线
费城中学 李晖
一、教学目标:
知识与技能:认识邻补角和对顶角;掌握对顶角相等,并会简单应用。
过程与方法:1.通过动手实践活动,探索邻补角与对顶角的位置和大小关系。
2.通过“对顶角相等”这个结论的简单推理,培养逻辑思维能力。
情感态度与价值观:通过探究活动来发现结论,经历知识的“再发现过程”,在探究活动中培养创新思维能力,体验数学学习的乐趣。
二、教学重点:邻补角、对顶角的概念,对顶角的性质与应用。
三、教学难点:理解对顶角相等的性质的探索。
四、教学过程设计:
问题与情境设计 师生活动设计
情景引入 多媒体演示某大桥画面。同学们,你们看这座宏伟的大桥,它的两端有很多斜拉的平行线,桥的侧面有许多相交线段组成的图案,这些都给我们以相交线、平行线的形象。两条直线相交能形成哪些角?这些角又有什么特征?课题: 5.1.1相交线(板书)。 通过学生熟悉的事物,直观形象地给出了生活中的平行线和相交线,激发了学生的学习兴趣。
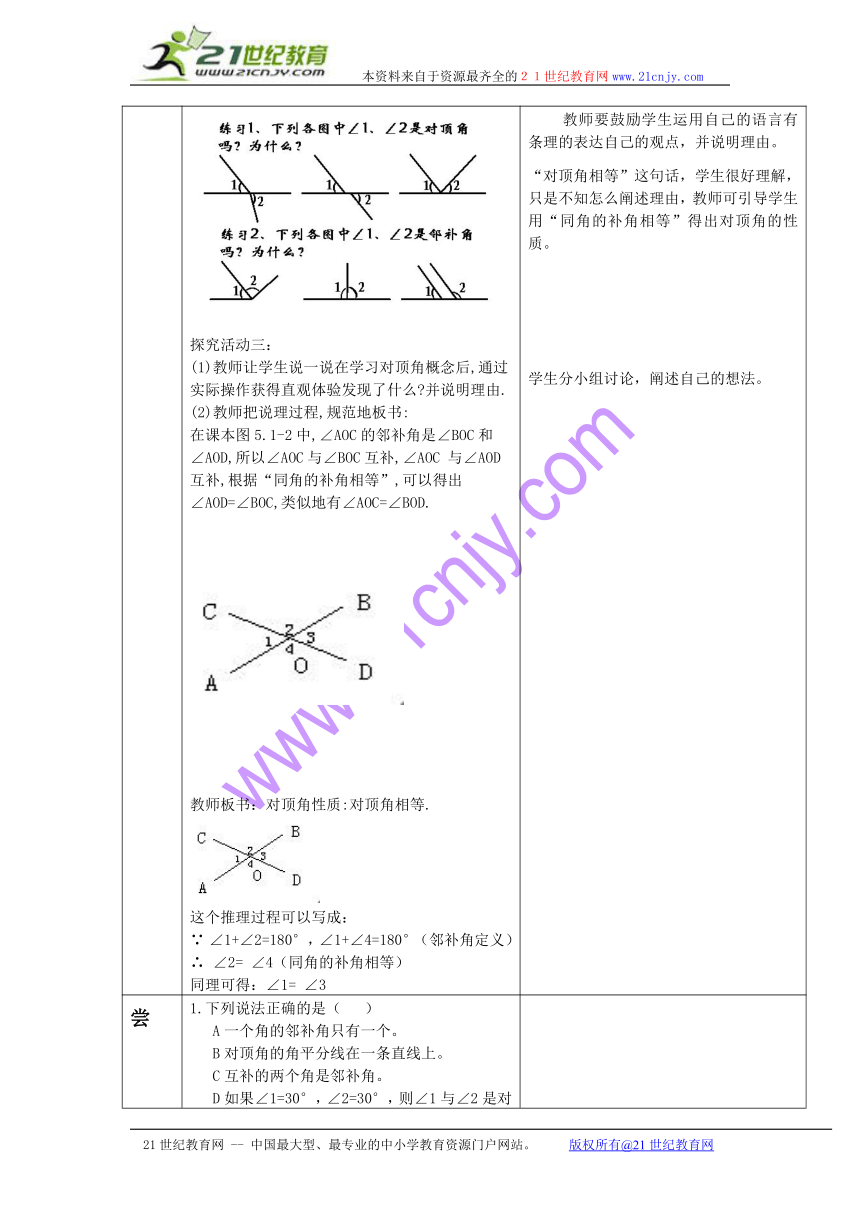
探究 探究活动一:教师出示一块布和一把剪刀,表演剪布过程,提出问题:剪布时,用力握紧把手,两个把手之间的的角发生了什么变化?剪刀张开的口又怎么变化? 探究活动二:1学生画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角?根据不同的位置怎么将它们分类?2.学生用量角器分别量一量各个角的度数,发现各类角的度数有什么关系。3.学生根据观察和度量完成下表:两直线相交形成的角分类位置关系数量关系 教师再提问:如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗 4.概括形成邻补角、对顶角概念.(1)师生共同定义邻补角、对顶角.有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.(2)识图训练:探究活动三:(1)教师让学生说一说在学习对顶角概念后,通过实际操作获得直观体验发现了什么 并说明理由.(2)教师把说理过程,规范地板书:在课本图5.1-2中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC 与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.教师板书:对顶角性质:对顶角相等.这个推理过程可以写成:∵ ∠1+∠2=180°,∠1+∠4=180°(邻补角定义)∴ ∠2= ∠4(同角的补角相等)同理可得:∠1= ∠3 教师动手操作,提出问题。学生观察、思考、回答问题。教师点评:如果把剪刀的构造看作是两条相交的直线,以上就关系到两条直线相交所成的角的问题。通过生活中的情景抽象出几何图形,培养空间观念,发展几何直觉。学生动手画图、思考并在小组内交流。当学生直观地感知角有“相邻”、“对顶”关系时, 教师引导学生用几何语言准确地表达。如: ∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线.∠AOC和∠BOD有公共的顶点O,而是∠AOC的两边分别是∠BOD两边的反向延长线.学生亲自动手测量,得出相应的关系,与小组成员交流结论。结论:有“相邻”关系的两角互补,“对顶”关系的两角相等,学生先独立完成然后师生共同纠正。小组成员讨论并回答。学生讨论不同的角的位置关系后,得出对顶角的定义,教师应提醒学生注意:①是两条直线相交而得;②有一个公共顶点;③没有公共边,三个条件缺一不可。教师放手让学生通过讨论解决问题,培养了学生的动手能力,提高了合作意识。教师要鼓励学生运用自己的语言有条理的表达自己的观点,并说明理由。“对顶角相等”这句话,学生很好理解,只是不知怎么阐述理由,教师可引导学生用“同角的补角相等”得出对顶角的性质。学生分小组讨论,阐述自己的想法。
尝试应用 1.下列说法正确的是( )A一个角的邻补角只有一个。B对顶角的角平分线在一条直线上。C互补的两个角是邻补角。D如果∠1=30°,∠2=30°,则∠1与∠2是对顶角。2.(1)如图,直线AB与CD 相交所成的四个角中,∠1的邻补角是 。∠2的对顶角是 。(2)上图中,若∠1=40°,则∠2= ,∠3= ,∠4= 。(3)若∠1=90°,∠2,∠3,∠4各等于多少度? 学生审题识图,分清角的关系,小组交流用什么途径去求这些未知角的度数?通过具体问题,强化学生对概念及性质的理解,并培养学生的说理习惯,发展符号感,逐步培养学生用几何语言交流的能力。尝试练习后教师板书出规范的求解过程。
补偿提高 1.已知两条直线相交而成的四个角,其中的一个角为50°,则其余三个角的度数分别是 。2如图所示,直线AB,CD交与O,OE是∠BOC的平分线,且∠BOE=50度,那么∠BOC= 度。(A) 80 ( B) 100 ( C) 130 ( D) 1503. 如图所示,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,求∠DOF的度数。
小结与作业 小结:通过本节课的学习,你有什么收获?作业:1.必做题课本第9页 习题5.1 2,7
2、选做题直线AB、CD、EF相交于点O, 若∠AOC:∠AOE=2:3,∠EOD=130°,求∠BOC的度数? 学生组内交流,归纳,补充。发挥学生的主体意识,培养学生的归纳能力学生可以根据自己的不同水平选择不同的作业,这样可为为学生提供个性化发展的空间。教师应及时了解学生的学习效果,使学生养成独立思考,反思学习过程的习惯。
达标测评题
1、 选择题
1.下列说法正确的是( )
A、有公共顶点的两个角是对顶角
B、相等的两角是对顶角
C、有公共顶点并且相等的角是对顶角
D、两条直线相交成的四个角中,有公共顶点且没有公共边的两个角是对顶角。
二.填空:
2.如图,直线AB与CD相交于点O,已知∠AOC+∠BOD=90°,则∠BOC= 。
3.已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3= 。
三.解答题
4如图所示,直线ABCDEF相交于点O,
(1) 写出∠AOC, ∠BOE的邻补角。
(2) 写出∠DOA, ∠BOF的对顶角。
(3) 如果∠AOE=30°,求∠BOF,∠AOF的度数。
5.如果直线AB、CD相交于O点,且∠AOC=28°,作∠DOE=∠DOB,OF平分∠AOE,求∠EOF的度数
附达标测评题答案:
1.D
2.135°
3.180°
4.(1)∠AOD、∠COB;∠AOE、∠BOF
(2)∠BOC、∠AOE
(3)30°、150°
5.62°
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新授课
七年级数学学科(下册)
5.1.1相交线
费城中学 李晖
一、教学目标:
知识与技能:认识邻补角和对顶角;掌握对顶角相等,并会简单应用。
过程与方法:1.通过动手实践活动,探索邻补角与对顶角的位置和大小关系。
2.通过“对顶角相等”这个结论的简单推理,培养逻辑思维能力。
情感态度与价值观:通过探究活动来发现结论,经历知识的“再发现过程”,在探究活动中培养创新思维能力,体验数学学习的乐趣。
二、教学重点:邻补角、对顶角的概念,对顶角的性质与应用。
三、教学难点:理解对顶角相等的性质的探索。
四、教学过程设计:
问题与情境设计 师生活动设计
情景引入 多媒体演示某大桥画面。同学们,你们看这座宏伟的大桥,它的两端有很多斜拉的平行线,桥的侧面有许多相交线段组成的图案,这些都给我们以相交线、平行线的形象。两条直线相交能形成哪些角?这些角又有什么特征?课题: 5.1.1相交线(板书)。 通过学生熟悉的事物,直观形象地给出了生活中的平行线和相交线,激发了学生的学习兴趣。
探究 探究活动一:教师出示一块布和一把剪刀,表演剪布过程,提出问题:剪布时,用力握紧把手,两个把手之间的的角发生了什么变化?剪刀张开的口又怎么变化? 探究活动二:1学生画直线AB、CD相交于点O,并说出图中4个角,两两相配共能组成几对角?根据不同的位置怎么将它们分类?2.学生用量角器分别量一量各个角的度数,发现各类角的度数有什么关系。3.学生根据观察和度量完成下表:两直线相交形成的角分类位置关系数量关系 教师再提问:如果改变∠AOC的大小, 会改变它与其它角的位置关系和数量关系吗 4.概括形成邻补角、对顶角概念.(1)师生共同定义邻补角、对顶角.有一条公共边,而且另一边互为反向延长线的两个角叫做邻补角.如果两个角有一个公共顶点, 而且一个角的两边分别是另一角两边的反向延长线,那么这两个角叫对顶角.(2)识图训练:探究活动三:(1)教师让学生说一说在学习对顶角概念后,通过实际操作获得直观体验发现了什么 并说明理由.(2)教师把说理过程,规范地板书:在课本图5.1-2中,∠AOC的邻补角是∠BOC和∠AOD,所以∠AOC与∠BOC互补,∠AOC 与∠AOD互补,根据“同角的补角相等”,可以得出∠AOD=∠BOC,类似地有∠AOC=∠BOD.教师板书:对顶角性质:对顶角相等.这个推理过程可以写成:∵ ∠1+∠2=180°,∠1+∠4=180°(邻补角定义)∴ ∠2= ∠4(同角的补角相等)同理可得:∠1= ∠3 教师动手操作,提出问题。学生观察、思考、回答问题。教师点评:如果把剪刀的构造看作是两条相交的直线,以上就关系到两条直线相交所成的角的问题。通过生活中的情景抽象出几何图形,培养空间观念,发展几何直觉。学生动手画图、思考并在小组内交流。当学生直观地感知角有“相邻”、“对顶”关系时, 教师引导学生用几何语言准确地表达。如: ∠AOC和∠BOC有一条公共边OC,它们的另一边互为反向延长线.∠AOC和∠BOD有公共的顶点O,而是∠AOC的两边分别是∠BOD两边的反向延长线.学生亲自动手测量,得出相应的关系,与小组成员交流结论。结论:有“相邻”关系的两角互补,“对顶”关系的两角相等,学生先独立完成然后师生共同纠正。小组成员讨论并回答。学生讨论不同的角的位置关系后,得出对顶角的定义,教师应提醒学生注意:①是两条直线相交而得;②有一个公共顶点;③没有公共边,三个条件缺一不可。教师放手让学生通过讨论解决问题,培养了学生的动手能力,提高了合作意识。教师要鼓励学生运用自己的语言有条理的表达自己的观点,并说明理由。“对顶角相等”这句话,学生很好理解,只是不知怎么阐述理由,教师可引导学生用“同角的补角相等”得出对顶角的性质。学生分小组讨论,阐述自己的想法。
尝试应用 1.下列说法正确的是( )A一个角的邻补角只有一个。B对顶角的角平分线在一条直线上。C互补的两个角是邻补角。D如果∠1=30°,∠2=30°,则∠1与∠2是对顶角。2.(1)如图,直线AB与CD 相交所成的四个角中,∠1的邻补角是 。∠2的对顶角是 。(2)上图中,若∠1=40°,则∠2= ,∠3= ,∠4= 。(3)若∠1=90°,∠2,∠3,∠4各等于多少度? 学生审题识图,分清角的关系,小组交流用什么途径去求这些未知角的度数?通过具体问题,强化学生对概念及性质的理解,并培养学生的说理习惯,发展符号感,逐步培养学生用几何语言交流的能力。尝试练习后教师板书出规范的求解过程。
补偿提高 1.已知两条直线相交而成的四个角,其中的一个角为50°,则其余三个角的度数分别是 。2如图所示,直线AB,CD交与O,OE是∠BOC的平分线,且∠BOE=50度,那么∠BOC= 度。(A) 80 ( B) 100 ( C) 130 ( D) 1503. 如图所示,AB⊥CD于点O,直线EF过点O,若∠AOE=65°,求∠DOF的度数。
小结与作业 小结:通过本节课的学习,你有什么收获?作业:1.必做题课本第9页 习题5.1 2,7
2、选做题直线AB、CD、EF相交于点O, 若∠AOC:∠AOE=2:3,∠EOD=130°,求∠BOC的度数? 学生组内交流,归纳,补充。发挥学生的主体意识,培养学生的归纳能力学生可以根据自己的不同水平选择不同的作业,这样可为为学生提供个性化发展的空间。教师应及时了解学生的学习效果,使学生养成独立思考,反思学习过程的习惯。
达标测评题
1、 选择题
1.下列说法正确的是( )
A、有公共顶点的两个角是对顶角
B、相等的两角是对顶角
C、有公共顶点并且相等的角是对顶角
D、两条直线相交成的四个角中,有公共顶点且没有公共边的两个角是对顶角。
二.填空:
2.如图,直线AB与CD相交于点O,已知∠AOC+∠BOD=90°,则∠BOC= 。
3.已知∠1与∠2是对顶角,∠1与∠3互为补角,则∠2+∠3= 。
三.解答题
4如图所示,直线ABCDEF相交于点O,
(1) 写出∠AOC, ∠BOE的邻补角。
(2) 写出∠DOA, ∠BOF的对顶角。
(3) 如果∠AOE=30°,求∠BOF,∠AOF的度数。
5.如果直线AB、CD相交于O点,且∠AOC=28°,作∠DOE=∠DOB,OF平分∠AOE,求∠EOF的度数
附达标测评题答案:
1.D
2.135°
3.180°
4.(1)∠AOD、∠COB;∠AOE、∠BOF
(2)∠BOC、∠AOE
(3)30°、150°
5.62°
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
