5.1.3 同位角、内错角、同旁内角
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角 |

|
|
| 格式 | rar | ||
| 文件大小 | 246.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-07 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新授课
七年级数学(下册)
5.1.3 同位角、内错角、同旁内角
费城中学 李晖
一、教学目标:
知识与技能:
1.使学生理解三线八角的意义,并能从复杂图形中识别它们.
2.通过三线八角的特点的分析,培养学生抽象概括问题的能力.
3.使学生认识图形是由简到繁组合而成,培养学生形成基本图形结构的能力
过程与方法:会借助大量三线八角素材识别同位角、内错角、同旁内角。
情感态度与价值观:在活动中培养学生乐于探索、合作学习的习惯,培养学生“用数学”的意识和能力。
二、教学重点: 已知两直线和截线,判断同位角、内错角、同旁内角
三、教学难点:已知两个角,要判别是哪两条直线被第3条直线所截而形成的什么位置关系的角。.
四、教学过程设计:
问题与情境设计 师生活动设计
情景引入 (1)平面上的两条直线有相交和平行两种位置关系,两直线相交形成几个角?称之为什么角?(2)在实际生活中,还存在着两条直线被第3条直线所截的情况,如斜拉桥的灯柱子与其横梁,脚手架的钢管,交通线路中的道路,将这些事物抽象成几何图形,就是如图所示的图形。(3)两条直线被第3条直线所截形成几个角 这8个角中有多种关系,如∠2与∠4,∠5与∠7,∠6与∠8, ∠1和∠3是对顶角,除了对顶角,还有没有其它新的关系的角呢 这节课我们就来研究同位角,内错角,同旁内角。 小组内讨论交流。让学生讨论后回答自己的想法。教师适当点拨,进而引出课题。
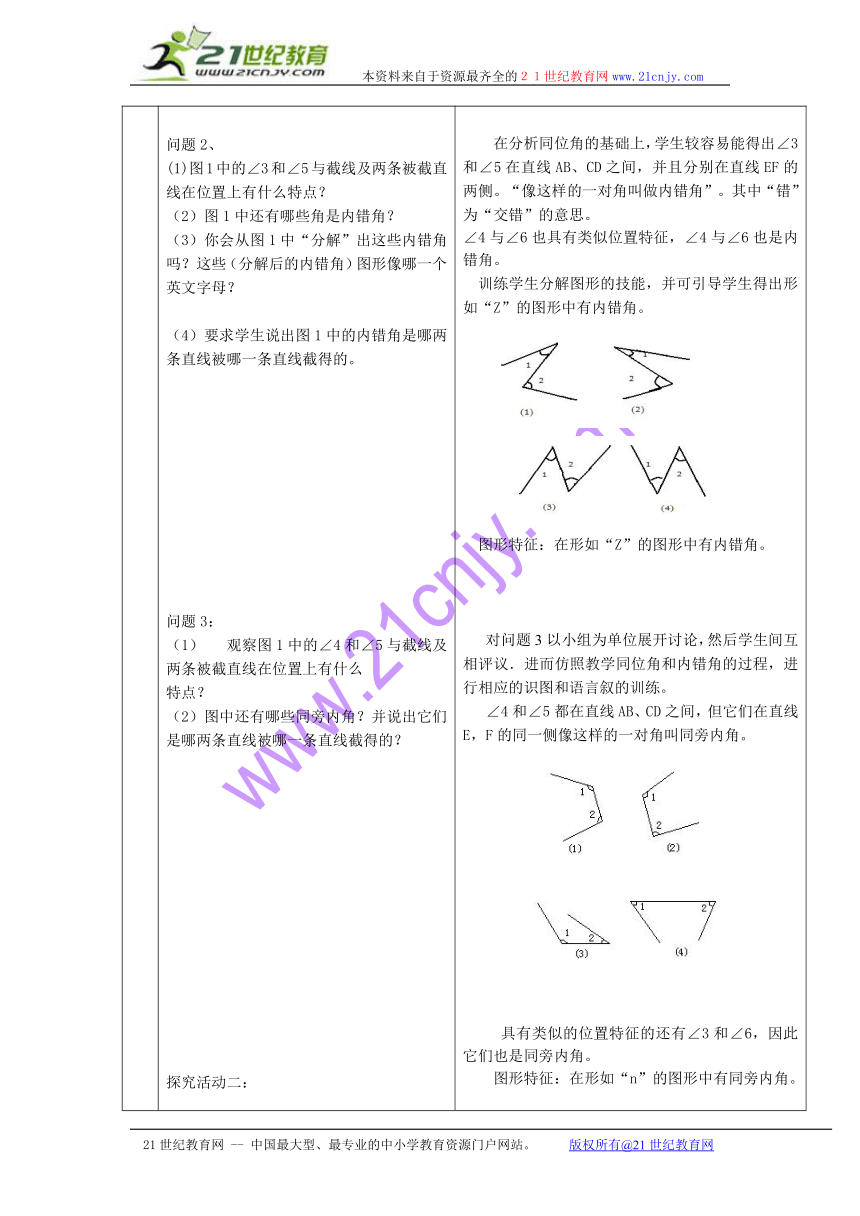
自主探究 探究活动一问题1.(1)如图1,怎样描述直线AB、CD和EF的位置关系? 图1(2)观察图1中的∠1和∠5与截线及两条被截直线在位置上有什么特点? (3)你还能在图1中找出其他的同位角吗?一共有几对? (5)你能看出两个同位角的边与边之间有什么关系吗?问题2、(1)图1中的∠3和∠5与截线及两条被截直线在位置上有什么特点? (2)图1中还有哪些角是内错角? (3)你会从图1中“分解”出这些内错角吗?这些(分解后的内错角)图形像哪一个英文字母? (4)要求学生说出图1中的内错角是哪两条直线被哪一条直线截得的。 问题3:(1) 观察图1中的∠4和∠5与截线及两条被截直线在位置上有什么特点? (2)图中还有哪些同旁内角?并说出它们是哪两条直线被哪一条直线截得的? 探究活动二:问题:(1)同位角和同旁内角在位置上有什么相同点和不同点?(2)内错角和同旁内角在位置上有什么相同点和不同点?(3)这三类角的共同特征是什么?探究活动三做一做(请一位学生上台展示学习成果)请用三根竹条或小木棍制作一个风筝骨架,观察风筝骨架中(图自己画)有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角 学生讨论、回答:直线AB、CD被直线EF所截。引导学生观察得出这两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同一侧(右侧),这是“同位角”的本质属性。然后,可以用“位置相同”来描述这种位置关系,给出“同位角”的描述性定义。 像这样位置相同的一对角叫做同位角。如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角互为同位角的两个角没有公共顶点和公共边,但有一条边在同一条直线上,然后将上述互为同位角的两个角,从图1中分解出来,画出如下图的草图,从这些简单图形中容易识别出∠1和∠2都是同位角。 图形特征:形如“F”的图形中有同位角。这就是把复杂图形“分解”为简单图形的训练,这种训练能有效地帮助学生掌握识图技能,从而扫除学生识别内错角、同旁内角时可能存在的障碍。 此外,还要训练学生用规范的几何语言描述;如图1中,∠1和∠5是“直线AB和直线CD被直线EF所截得的“同位角”。 在分析同位角的基础上,学生较容易能得出∠3和∠5在直线AB、CD之间,并且分别在直线EF的两侧。“像这样的一对角叫做内错角”。其中“错”为“交错”的意思。 ∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。训练学生分解图形的技能,并可引导学生得出形如“Z”的图形中有内错角。图形特征:在形如“Z”的图形中有内错角。对问题3以小组为单位展开讨论,然后学生间互相评议.进而仿照教学同位角和内错角的过程,进行相应的识图和语言叙的训练。 ∠4和∠5都在直线AB、CD之间,但它们在直线E,F的同一侧像这样的一对角叫同旁内角。 具有类似的位置特征的还有∠3和∠6,因此它们也是同旁内角。图形特征:在形如“n”的图形中有同旁内角。学生组内交流讨论,教师 ( http: / / www.21cnjy.com / " \t "_blank )对学生讨论过程中所发表的意见进行评判,归纳总结.提醒学生:截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中的主线是截线,抓住了截线,再利用在图形结特征(F、Z、U)判断问题就迎刃而解. 让学生自己尝试学习,可以充分发挥学生的积极性、主动性和创造性,几个问题的设计目的是深化教学重点,使学生看书更具有针对性,避免盲目性.学生互相评价可以增加讨论的深度,教师最后评价可以统一学生的观点,学生在议议评评的过程中明理、增智,培养了能力. 根据学生的分析,教师在多媒体上出示表格帮助学生归纳。让学生亲自动手,可增添学生学习的兴趣,在实践中体会这三个角各自的特点归纳:寻找同位角,内错角,同旁内角关键要分清两条直线和截线,然后按相互的位置特征进行判别。
尝试应用 1.如图1,下列说法中错误的是( )
A.∠2与∠6是同位角
B.∠2与∠5是同旁内角
C.∠3与∠5是内错角
D.∠4与∠7是同位角2.如图,∠6和∠2是_________角,∠5和∠6是_________角,∠5和∠7是_________角,∠1和∠5是_________角,∠4和∠6是_________角,∠3和∠1是_________角。 3.如图,∠B的内错角、同旁内角各有哪些?请分别写出来。 本组练习是由“三线八角”图形判断同位角、内错角、同旁内角.这需要进行以下三个步骤,一看角的顶点;二看角的边;三看角的方位.这“三看”又离不开主线——截线的确定,让学生知道:无论图形的位置怎样变动,图形多么复杂,都要以截线为主线(不变),去解决万变的图形,另外遇到较复杂的图形,也可以从分解图形入手,把复杂图形化为若干个基本图形.
补偿提高 3如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
小结与作业 小结:这节课你有哪些收获?作业:必做题课本第7页练习1、2题选做题如图所示,直线AB截直线CD和EF,构成8个角,指出图中的同位角,内错角,同旁内角。 通过小结,帮助学生全面地理 ( http: / / www.21cnjy.com / " \t "_blank )解掌握所学知识,使知识成为“体系”从而形成新的认知结构。让学有余力的学生进一步做选做题,目的是调动学生的学习和积极性,提高学生思维广度,培养学生良好的学习习惯和思维方式。
达标测评题
1、 选择题
1如图,下列说法错误的是( )
A.∠1和∠B是同位角
B.∠2与∠B是同位角
C.∠2与∠C是内错角
D.∠EAC与∠C是内错角。
二、填空题
2.如图所示:
三、解答题:
3.如图所示,在∠1、∠2、∠3、∠4、∠A、∠C、∠ABC、∠ADC中,找出所有的内错角和同旁内角。
附:检测题答案
1.B
2.(1)DE、BC、AC、同位角;
(2)∠EBC、EB;∠EDB、∠DBC;
(3)∠ABE、∠BEC
3.内错角:∠1和∠4、∠2和∠3;
同旁内角:∠1和∠3、∠1和∠C、∠3和∠C、∠2和∠4、∠2和∠A、∠4和∠A、
∠A和∠ADC、∠A和∠ABC、∠C和∠ABC、∠C和∠ADC。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新授课
七年级数学(下册)
5.1.3 同位角、内错角、同旁内角
费城中学 李晖
一、教学目标:
知识与技能:
1.使学生理解三线八角的意义,并能从复杂图形中识别它们.
2.通过三线八角的特点的分析,培养学生抽象概括问题的能力.
3.使学生认识图形是由简到繁组合而成,培养学生形成基本图形结构的能力
过程与方法:会借助大量三线八角素材识别同位角、内错角、同旁内角。
情感态度与价值观:在活动中培养学生乐于探索、合作学习的习惯,培养学生“用数学”的意识和能力。
二、教学重点: 已知两直线和截线,判断同位角、内错角、同旁内角
三、教学难点:已知两个角,要判别是哪两条直线被第3条直线所截而形成的什么位置关系的角。.
四、教学过程设计:
问题与情境设计 师生活动设计
情景引入 (1)平面上的两条直线有相交和平行两种位置关系,两直线相交形成几个角?称之为什么角?(2)在实际生活中,还存在着两条直线被第3条直线所截的情况,如斜拉桥的灯柱子与其横梁,脚手架的钢管,交通线路中的道路,将这些事物抽象成几何图形,就是如图所示的图形。(3)两条直线被第3条直线所截形成几个角 这8个角中有多种关系,如∠2与∠4,∠5与∠7,∠6与∠8, ∠1和∠3是对顶角,除了对顶角,还有没有其它新的关系的角呢 这节课我们就来研究同位角,内错角,同旁内角。 小组内讨论交流。让学生讨论后回答自己的想法。教师适当点拨,进而引出课题。
自主探究 探究活动一问题1.(1)如图1,怎样描述直线AB、CD和EF的位置关系? 图1(2)观察图1中的∠1和∠5与截线及两条被截直线在位置上有什么特点? (3)你还能在图1中找出其他的同位角吗?一共有几对? (5)你能看出两个同位角的边与边之间有什么关系吗?问题2、(1)图1中的∠3和∠5与截线及两条被截直线在位置上有什么特点? (2)图1中还有哪些角是内错角? (3)你会从图1中“分解”出这些内错角吗?这些(分解后的内错角)图形像哪一个英文字母? (4)要求学生说出图1中的内错角是哪两条直线被哪一条直线截得的。 问题3:(1) 观察图1中的∠4和∠5与截线及两条被截直线在位置上有什么特点? (2)图中还有哪些同旁内角?并说出它们是哪两条直线被哪一条直线截得的? 探究活动二:问题:(1)同位角和同旁内角在位置上有什么相同点和不同点?(2)内错角和同旁内角在位置上有什么相同点和不同点?(3)这三类角的共同特征是什么?探究活动三做一做(请一位学生上台展示学习成果)请用三根竹条或小木棍制作一个风筝骨架,观察风筝骨架中(图自己画)有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角 学生讨论、回答:直线AB、CD被直线EF所截。引导学生观察得出这两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同一侧(右侧),这是“同位角”的本质属性。然后,可以用“位置相同”来描述这种位置关系,给出“同位角”的描述性定义。 像这样位置相同的一对角叫做同位角。如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角互为同位角的两个角没有公共顶点和公共边,但有一条边在同一条直线上,然后将上述互为同位角的两个角,从图1中分解出来,画出如下图的草图,从这些简单图形中容易识别出∠1和∠2都是同位角。 图形特征:形如“F”的图形中有同位角。这就是把复杂图形“分解”为简单图形的训练,这种训练能有效地帮助学生掌握识图技能,从而扫除学生识别内错角、同旁内角时可能存在的障碍。 此外,还要训练学生用规范的几何语言描述;如图1中,∠1和∠5是“直线AB和直线CD被直线EF所截得的“同位角”。 在分析同位角的基础上,学生较容易能得出∠3和∠5在直线AB、CD之间,并且分别在直线EF的两侧。“像这样的一对角叫做内错角”。其中“错”为“交错”的意思。 ∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。训练学生分解图形的技能,并可引导学生得出形如“Z”的图形中有内错角。图形特征:在形如“Z”的图形中有内错角。对问题3以小组为单位展开讨论,然后学生间互相评议.进而仿照教学同位角和内错角的过程,进行相应的识图和语言叙的训练。 ∠4和∠5都在直线AB、CD之间,但它们在直线E,F的同一侧像这样的一对角叫同旁内角。 具有类似的位置特征的还有∠3和∠6,因此它们也是同旁内角。图形特征:在形如“n”的图形中有同旁内角。学生组内交流讨论,教师 ( http: / / www.21cnjy.com / " \t "_blank )对学生讨论过程中所发表的意见进行评判,归纳总结.提醒学生:截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中的主线是截线,抓住了截线,再利用在图形结特征(F、Z、U)判断问题就迎刃而解. 让学生自己尝试学习,可以充分发挥学生的积极性、主动性和创造性,几个问题的设计目的是深化教学重点,使学生看书更具有针对性,避免盲目性.学生互相评价可以增加讨论的深度,教师最后评价可以统一学生的观点,学生在议议评评的过程中明理、增智,培养了能力. 根据学生的分析,教师在多媒体上出示表格帮助学生归纳。让学生亲自动手,可增添学生学习的兴趣,在实践中体会这三个角各自的特点归纳:寻找同位角,内错角,同旁内角关键要分清两条直线和截线,然后按相互的位置特征进行判别。
尝试应用 1.如图1,下列说法中错误的是( )
A.∠2与∠6是同位角
B.∠2与∠5是同旁内角
C.∠3与∠5是内错角
D.∠4与∠7是同位角2.如图,∠6和∠2是_________角,∠5和∠6是_________角,∠5和∠7是_________角,∠1和∠5是_________角,∠4和∠6是_________角,∠3和∠1是_________角。 3.如图,∠B的内错角、同旁内角各有哪些?请分别写出来。 本组练习是由“三线八角”图形判断同位角、内错角、同旁内角.这需要进行以下三个步骤,一看角的顶点;二看角的边;三看角的方位.这“三看”又离不开主线——截线的确定,让学生知道:无论图形的位置怎样变动,图形多么复杂,都要以截线为主线(不变),去解决万变的图形,另外遇到较复杂的图形,也可以从分解图形入手,把复杂图形化为若干个基本图形.
补偿提高 3如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?
小结与作业 小结:这节课你有哪些收获?作业:必做题课本第7页练习1、2题选做题如图所示,直线AB截直线CD和EF,构成8个角,指出图中的同位角,内错角,同旁内角。 通过小结,帮助学生全面地理 ( http: / / www.21cnjy.com / " \t "_blank )解掌握所学知识,使知识成为“体系”从而形成新的认知结构。让学有余力的学生进一步做选做题,目的是调动学生的学习和积极性,提高学生思维广度,培养学生良好的学习习惯和思维方式。
达标测评题
1、 选择题
1如图,下列说法错误的是( )
A.∠1和∠B是同位角
B.∠2与∠B是同位角
C.∠2与∠C是内错角
D.∠EAC与∠C是内错角。
二、填空题
2.如图所示:
三、解答题:
3.如图所示,在∠1、∠2、∠3、∠4、∠A、∠C、∠ABC、∠ADC中,找出所有的内错角和同旁内角。
附:检测题答案
1.B
2.(1)DE、BC、AC、同位角;
(2)∠EBC、EB;∠EDB、∠DBC;
(3)∠ABE、∠BEC
3.内错角:∠1和∠4、∠2和∠3;
同旁内角:∠1和∠3、∠1和∠C、∠3和∠C、∠2和∠4、∠2和∠A、∠4和∠A、
∠A和∠ADC、∠A和∠ABC、∠C和∠ABC、∠C和∠ADC。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
