(苏科版八年级上)数学:2.7勾股定理的应用同步练习
文档属性
| 名称 | (苏科版八年级上)数学:2.7勾股定理的应用同步练习 |  | |
| 格式 | rar | ||
| 文件大小 | 79.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-08 17:08:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2.7勾股定理的应用
姓名_____________班级____________学号____________分数_____________
一、选择题
1 .下列各组数中,以a,b,c为边的三角形不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=5
2 .四边形的四条边AB、BC、CD、DA的长分别为3、4、13、12,其中∠B=90°,则四边形的面积是 ( )
A.72 B.66 C.42 D.36[来源:21世纪教育网]
3 .已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
4 .如图,在Rt△ABC中,∠ACB=90O,BC=6,正方形ABDE的面积为100,则正方形ACFG的面积为( )
A.64 B.36 C.82 D.49
5 .如图2,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=5,在AC上取一E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )[21世纪教育网
A.1 B. C.2 D.
二、填空题
6 .已知,中,,则的面积为________.
7 .已知直角三角形的两边长分别为3和4,则第三边长为__________
8 .△ABC中,AB=AC=6,∠A=60°,BD为高,则BD=________.
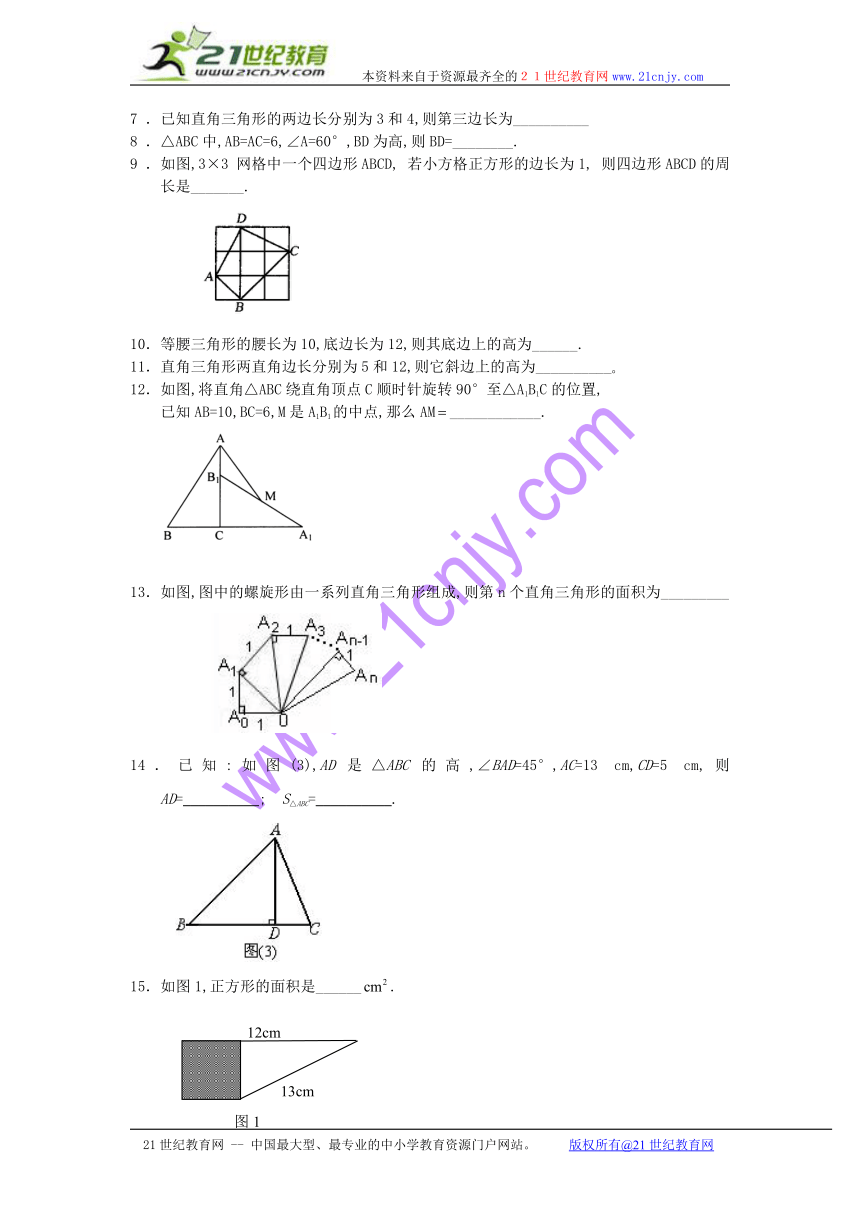
9 .如图,3×3网格中一个四边形ABCD,若小方格正方形的边长为1,则四边形ABCD的周长是_______.
10.等腰三角形的腰长为10,底边长为12,则其底边上的高为______.
11.直角三角形两直角边长分别为5和12,则它斜边上的高为__________
12.如图,将直角△ABC绕直角顶点C顺时针旋转90°至△A1B1C的位置,
已知AB=10,BC=6,M是A1B1的中点,那么AM____________.
13.如图,图中的螺旋形由一系列直角三角形组成,则第n个直角三角形的面积为_________
14.已知:如图(3),AD是△ABC的高,∠BAD=45°,AC=13 cm,CD=5 cm,则AD=__________;?S△ABC=__________.
?
15.如图1,正方形的面积是______.
三、解答题
16.如图9,在四边形中,,
,求四边形的面积
17.如图,中,于D,若求的长
18.一个三角形三条边的比为5∶12∶13,且周长为60cm,求它的面积.
19.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=900,试求∠A的度数
20.如图,要从电线杆离地面12米处向地面拉一条长为13米的钢缆,求地面钢缆固定点A到电线杆底部B的距离.
21.某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方
22.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n (n>1)的代数式表示:
a = ______,b = ______,c = ______.
(2)猜想:以a、b、c为边的三角形是否为直角三角形 并说明你的猜想.
23.木工师傅做一个人字形屋梁,如图所示,上弦AB=AC=4m,跨度BC为6m,现有一根长为3m的木料打算做中柱AD(AD是△ABC的中线),请你通过计算说明这根木料的长度是否适合做中柱AD.(只考虑长度、不计损耗)
24.木工师傅为了让直尺经久耐用,常常在直尺的直角顶点与斜边之间加一个小木条,如下左图所示.下右图为其示意图.若∠BAC=90°,线段AB的长为5,线段AC的长为12,试求出小木条AD的最短长度.[21世纪教育网
25.如图所示,正方形网格中的每个小正方形边长都是1,画出一个周长为5三角形,且使它的每个顶点都在小正方形的顶点上.判断你所画三角形的形状,并说明理由.
21世纪教育网
21世纪教育网
2.7勾股定理的应用参考答案
一、选择题
1 .A 2 .D 3 .A 4 .A 5 .B
二、填空题
6 . 7 .5或 8 .3
9 .3+2 [点拨]四边形ABCD的周长为+++ =3+2.
10.8; 11. 12. 13.
14.12 cm 102 cm2
15.25
三、解答题
16.解:连接AC,在中
在中,
所以直角三角形
17. ;
18.解:三角形的三边的长分别为:
60×=10厘米 60×=24厘米 60×=26厘米
∵102+242=676=262
∴此三角形是直角三角形
∴S= ×10×24=120厘米2
19.解:连接AC,在Rt△ABC中,AB=AC=2
∴ ∠BAC=450,AC2=AB2+BC2=22+22=8
在△DAC中,AD=1,DC=3
∴ AD2+AC2=8+12=9=32=CD2
∴ ∠DAC=900
∴ ∠DAB=∠BAC+∠DAC
=450+900
=1350
20.解:由已知有,在Rt△ABC中
BC=12,AC=13
AB2+BC2=AC2
∴ AB2=AC2-BC2=132-122=25
∴ AB=5
答:地面钢缆固定点A到电线杆底部B的距离为5米
21.解:设AE= x千米,则BE=(25-x)千米,
在Rt△DAE中,DA2+AE2=DE2
在Rt△EBC中,BE2+BC2=CE2
∵ CE=DE
∴ DA2+AE2 = BE2+BC2
∴ 152+x2=102+(25-x)2
解得:x=10千米 ∴ 基地应建在离A站10千米的地方
22.(1)n2-1 2 n n2+1
(2)答:以a、b、c为边的三角形是直角三角形
理由:因为a2+ b2=(n2-1)2+4 n2
= n4-2 n2+1+4 n2= n 4+2 n2+1=( n2+1)2=c2
所以以a、b、c为边的三角形是直角三角形
23..解:∵AB=CD=4 ,AD是△ABC的中线 ,BC=6,
∴AD⊥BC,BD=BC=3
由勾股定理,得
AD=
∵<3,∴这根木料的长度适合做中柱AD
24.当AD⊥BC时,小木条AD的长度最短
此时,因为∠BAC=90°,AB=5,AC=12,所以BC=13
因为三角形ABC的面积=AB×AC=BC×AD,所以AD=
答:小木条AD的最短长度为
25.解:如图,△ABC(或△A’B’C’等)就是所求的三角形.
△ABC是直角三角形.
∵AB=5,AC=,BC=.
∴AC 2 +BC 2 =,
AB 2 =52 =25,
∴AC 2 +BC 2 =AB 2.
∴△ABC是直角三角形.
A
E E
F
G
D
C
B
A
B
C
D
E
图2
图1
13cm
12cm
图9
A
B
D
C
A
D
E
B
C
A
C
B
D
A
B
C
D
A’
B’
C’
C
B
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2.7勾股定理的应用
姓名_____________班级____________学号____________分数_____________
一、选择题
1 .下列各组数中,以a,b,c为边的三角形不是Rt△的是( )
A、a=1.5,b=2,c=3 B、a=7,b=24,c=25 C、a=6,b=8,c=10 D、a=3,b=4,c=5
2 .四边形的四条边AB、BC、CD、DA的长分别为3、4、13、12,其中∠B=90°,则四边形的面积是 ( )
A.72 B.66 C.42 D.36[来源:21世纪教育网]
3 .已知,如图,长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、6cm2 B、8cm2 C、10cm2 D、12cm2
4 .如图,在Rt△ABC中,∠ACB=90O,BC=6,正方形ABDE的面积为100,则正方形ACFG的面积为( )
A.64 B.36 C.82 D.49
5 .如图2,在三角形纸片ABC中,∠ACB=90°,BC=3,AB=5,在AC上取一E,以BE为折痕,使AB的一部分与BC重合,A与BC延长线上的点D重合,则CE的长度为( )[21世纪教育网
A.1 B. C.2 D.
二、填空题
6 .已知,中,,则的面积为________.
7 .已知直角三角形的两边长分别为3和4,则第三边长为__________
8 .△ABC中,AB=AC=6,∠A=60°,BD为高,则BD=________.
9 .如图,3×3网格中一个四边形ABCD,若小方格正方形的边长为1,则四边形ABCD的周长是_______.
10.等腰三角形的腰长为10,底边长为12,则其底边上的高为______.
11.直角三角形两直角边长分别为5和12,则它斜边上的高为__________
12.如图,将直角△ABC绕直角顶点C顺时针旋转90°至△A1B1C的位置,
已知AB=10,BC=6,M是A1B1的中点,那么AM____________.
13.如图,图中的螺旋形由一系列直角三角形组成,则第n个直角三角形的面积为_________
14.已知:如图(3),AD是△ABC的高,∠BAD=45°,AC=13 cm,CD=5 cm,则AD=__________;?S△ABC=__________.
?
15.如图1,正方形的面积是______.
三、解答题
16.如图9,在四边形中,,
,求四边形的面积
17.如图,中,于D,若求的长
18.一个三角形三条边的比为5∶12∶13,且周长为60cm,求它的面积.
19.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,且∠ABC=900,试求∠A的度数
20.如图,要从电线杆离地面12米处向地面拉一条长为13米的钢缆,求地面钢缆固定点A到电线杆底部B的距离.
21.某镇为响应中央关于建设社会主义新农村的号召,决定公路相距25km的A,B两站之间E点修建一个土特产加工基地,如图,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要使C、D两村到E点的距离相等,那么基地E应建在离A站多少km的地方
22.张老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a 22-1 32-1 42-1 52-1 …
b 4 6 8 10 …
c 22+1 32+1 42+1 52+1 …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数n (n>1)的代数式表示:
a = ______,b = ______,c = ______.
(2)猜想:以a、b、c为边的三角形是否为直角三角形 并说明你的猜想.
23.木工师傅做一个人字形屋梁,如图所示,上弦AB=AC=4m,跨度BC为6m,现有一根长为3m的木料打算做中柱AD(AD是△ABC的中线),请你通过计算说明这根木料的长度是否适合做中柱AD.(只考虑长度、不计损耗)
24.木工师傅为了让直尺经久耐用,常常在直尺的直角顶点与斜边之间加一个小木条,如下左图所示.下右图为其示意图.若∠BAC=90°,线段AB的长为5,线段AC的长为12,试求出小木条AD的最短长度.[21世纪教育网
25.如图所示,正方形网格中的每个小正方形边长都是1,画出一个周长为5三角形,且使它的每个顶点都在小正方形的顶点上.判断你所画三角形的形状,并说明理由.
21世纪教育网
21世纪教育网
2.7勾股定理的应用参考答案
一、选择题
1 .A 2 .D 3 .A 4 .A 5 .B
二、填空题
6 . 7 .5或 8 .3
9 .3+2 [点拨]四边形ABCD的周长为+++ =3+2.
10.8; 11. 12. 13.
14.12 cm 102 cm2
15.25
三、解答题
16.解:连接AC,在中
在中,
所以直角三角形
17. ;
18.解:三角形的三边的长分别为:
60×=10厘米 60×=24厘米 60×=26厘米
∵102+242=676=262
∴此三角形是直角三角形
∴S= ×10×24=120厘米2
19.解:连接AC,在Rt△ABC中,AB=AC=2
∴ ∠BAC=450,AC2=AB2+BC2=22+22=8
在△DAC中,AD=1,DC=3
∴ AD2+AC2=8+12=9=32=CD2
∴ ∠DAC=900
∴ ∠DAB=∠BAC+∠DAC
=450+900
=1350
20.解:由已知有,在Rt△ABC中
BC=12,AC=13
AB2+BC2=AC2
∴ AB2=AC2-BC2=132-122=25
∴ AB=5
答:地面钢缆固定点A到电线杆底部B的距离为5米
21.解:设AE= x千米,则BE=(25-x)千米,
在Rt△DAE中,DA2+AE2=DE2
在Rt△EBC中,BE2+BC2=CE2
∵ CE=DE
∴ DA2+AE2 = BE2+BC2
∴ 152+x2=102+(25-x)2
解得:x=10千米 ∴ 基地应建在离A站10千米的地方
22.(1)n2-1 2 n n2+1
(2)答:以a、b、c为边的三角形是直角三角形
理由:因为a2+ b2=(n2-1)2+4 n2
= n4-2 n2+1+4 n2= n 4+2 n2+1=( n2+1)2=c2
所以以a、b、c为边的三角形是直角三角形
23..解:∵AB=CD=4 ,AD是△ABC的中线 ,BC=6,
∴AD⊥BC,BD=BC=3
由勾股定理,得
AD=
∵<3,∴这根木料的长度适合做中柱AD
24.当AD⊥BC时,小木条AD的长度最短
此时,因为∠BAC=90°,AB=5,AC=12,所以BC=13
因为三角形ABC的面积=AB×AC=BC×AD,所以AD=
答:小木条AD的最短长度为
25.解:如图,△ABC(或△A’B’C’等)就是所求的三角形.
△ABC是直角三角形.
∵AB=5,AC=,BC=.
∴AC 2 +BC 2 =,
AB 2 =52 =25,
∴AC 2 +BC 2 =AB 2.
∴△ABC是直角三角形.
A
E E
F
G
D
C
B
A
B
C
D
E
图2
图1
13cm
12cm
图9
A
B
D
C
A
D
E
B
C
A
C
B
D
A
B
C
D
A’
B’
C’
C
B
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
