江苏省徐州六县2010-2011学年度第一学期期中考试高二数学试题(文科)
文档属性
| 名称 | 江苏省徐州六县2010-2011学年度第一学期期中考试高二数学试题(文科) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-10 00:00:00 | ||
图片预览


文档简介
江苏省徐州六县2010~2011学年度第一学期期中考试试卷
高二数学(选修历史)
参考公式:
锥体的体积公式:,其中S是锥体的底面面积,是高。
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.“”是 ▲ 命题.(填写“真”或“假”)
2. 若平面与平面相交于直线,直线与直线相交于点,则直线与平面的公共点的个数可能为 ▲ .
3. 直线的倾斜角大小为 ▲ .
4. 若点B是关于坐标平面的对称点,则AB= ▲ .
5. 过两点的直线的方程的一般式为 ▲ .
6. 已知圆C的圆心坐标为,一条直径的两个端点分别在轴和轴上,则圆C 的标准方程为 ▲ .
7. “”是“函数是R上的奇函数”的 ▲ 条件.(填写“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
8. 空间三条直线.下列正确命题的序号是 ▲ .
①若,则;
②若,则;
③过空间一点有且只有一条直线与直线成60°角;
④与两条异面直线都垂直的直线有无数条.
9. 与直线切于点,且经过点的圆的方程为 ▲ .
10. 下列命题正确的序号是 ▲ .(其中表示直线,表示平面)
①若;
②若;
③若;
④若.
11. 已知点和点分别在直线的两侧,则实数的取值范围为
▲ .
12. 正方体的棱长为,若过作平面,则截面三角形的面积为 ▲ .
13. 在三棱锥中,侧棱、、两两垂直且长度均为,点在上,且,则的值为 ▲ .
14. 若△ABC的一个顶点,的平分线分别为,则直线BC的方程为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分14分)
已知直线和.
(1)若和相交于点,求、的值;
(2)若,求、的值;
(3)若点到直线的距离为1,求的值.
16.(本题满分14分)
如图,已知一个圆锥的底面半径为,高为,在其中有一个高为的内接圆柱(其中均为常数).
(1)当时,求内接圆柱上方的圆锥的体积;
(2)当为何值时,这个内接圆柱的侧面积最大?
并求出其最大值。
17.(本题满分14分)
如图已知在三棱柱ABC——A1B1C1中,AA1⊥平面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
(1)求证:平面平面;
(2)求证:平面PCC1⊥平面MNQ.
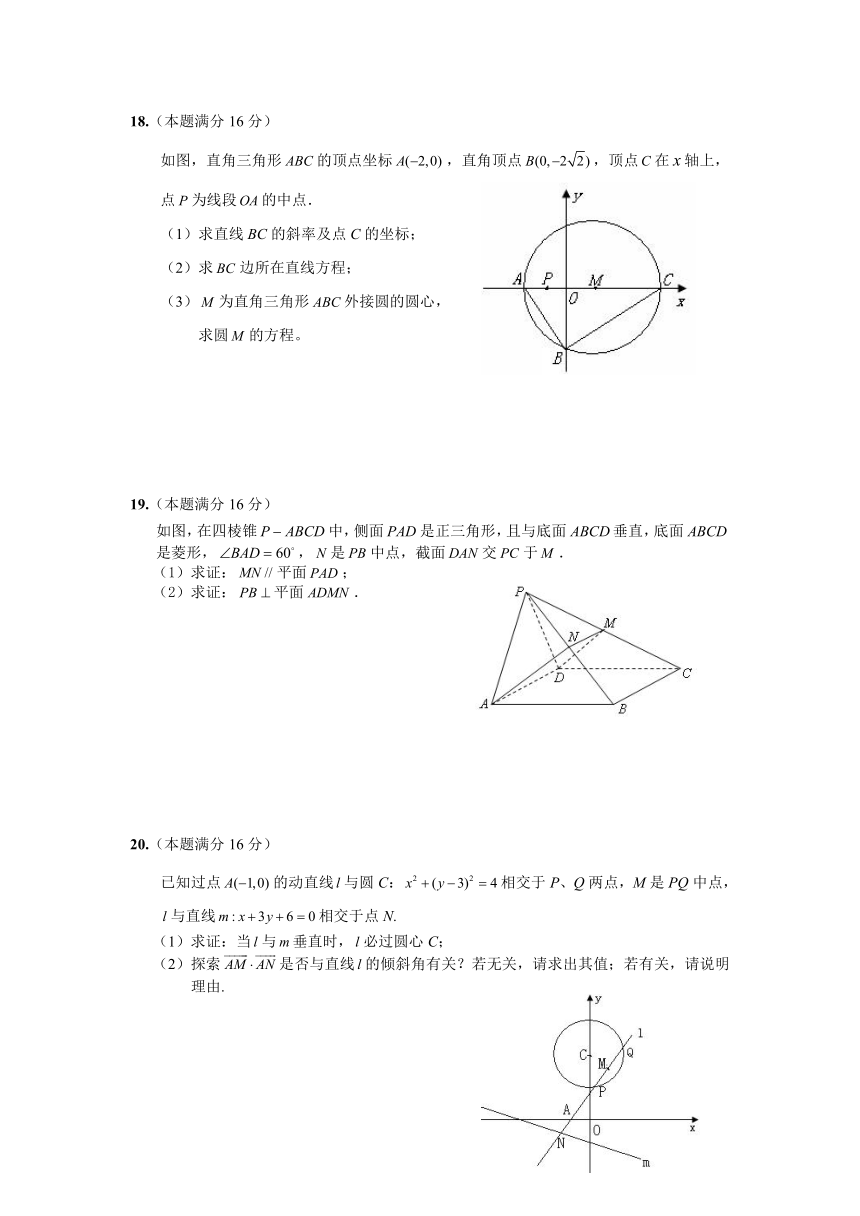
18.(本题满分16分)
如图,直角三角形的顶点坐标,直角顶点,顶点在轴上,点为线段的中点.
(1)求直线BC的斜率及点C的坐标;
(2)求边所在直线方程;
(3)为直角三角形外接圆的圆心,
求圆的方程。
19.(本题满分16分)
如图,在四棱锥中,侧面是正三角形,且与底面垂直,底面是菱形,,是中点,截面交于.
(1)求证:平面;
(2)求证:平面.
20.(本题满分16分)
已知过点的动直线与圆C:相交于P、Q两点,M是PQ中点,与直线相交于点N.
(1)求证:当与垂直时,必过圆心C;
(2)探索是否与直线的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
高二数学(选修历史)参考答案及评分标准
一、填空题
1.假; 2.1个或无数个; 3.120°; 4.6; 5.;
6.; 7.必要不充分; 8.②和④; 9.
10.①、③、④; 11.(-19,-9); 12.; 13.; 14..
二、解答题
15.解:(1)由题意得解得 (4分)
(2)由得或 (10分)
(3)由题意得,解得. (14分)
16.解:圆锥、圆柱的轴截面如图所示,其中
设圆柱底面半径为,则 (3分)
(1)当时,
∴ (8分)
(2)设圆柱的侧面积为.
∵,
∴ (10分)
(12分)
∴当时,. (14分)
17.证明:(1)∵分别是的中点,
∴ (1分)
又∵平面,平面,
∴平面 (4分)
∵平面平面,
∴平面. (5分)
又∵,
∴平面平面. (7分)
(2)∵AC=BC, P是AB的中点,∴AB⊥PC (8分)
∵AA1⊥面ABC,CC1∥AA1,∴CC1⊥面ABC,
而AB在平面ABC内,∴CC1⊥AB, (9分)
∵CC1∩PC=C ∴AB⊥面PCC1; (10分)
又∵M、N分别是AA1、BB1的中点,四边形AA1B1B是平行四边形,MN∥AB,
∴MN⊥面PCC1 (12分)
∵MN在平面MNQ内,∴面PCC1⊥面MNQ; (14分)
18.解:(1)∵,,∴ (3分)
由两点间距离公式得,
由△OAB∽△OBC,得,可求得,
于是在Rt△OBC中可求得,∴ (7分)
(2),由点斜式或两点式可求得.(11分)
(3)在上式中,令,得,∴圆心
又∵,∴外接圆的方程为. (16分)
19.证明:(1),
∴。 (3分)
又∵,,
∴。 (6分)
而,∴ (9分)
(2)取AD中点O,连结BO,BD。
在中,∵,∴ (10分)
在△ABD中,∵AD=AB,,
∴三角形ABD为等边三角形,∴ (11分)
又,,
∴,∴ (14分)
又∵,∴ (16分)
20.解:(1)∵,且,
∴.
故直线的方程为,即 (5分)
∵圆心坐标满足直线的方程,
∴当时,必过圆心C. (7分)
(2)∵,
∴=(9分)
①当轴时,易得,
则 (10分)
又,
∴ (12分)
②当与轴不垂直时,设直线的方程为
,则由得,则 (14分)
∴.
综上所述,与直线的斜率无关,且 (16分)
高二数学(选修历史)
参考公式:
锥体的体积公式:,其中S是锥体的底面面积,是高。
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.
1.“”是 ▲ 命题.(填写“真”或“假”)
2. 若平面与平面相交于直线,直线与直线相交于点,则直线与平面的公共点的个数可能为 ▲ .
3. 直线的倾斜角大小为 ▲ .
4. 若点B是关于坐标平面的对称点,则AB= ▲ .
5. 过两点的直线的方程的一般式为 ▲ .
6. 已知圆C的圆心坐标为,一条直径的两个端点分别在轴和轴上,则圆C 的标准方程为 ▲ .
7. “”是“函数是R上的奇函数”的 ▲ 条件.(填写“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”)
8. 空间三条直线.下列正确命题的序号是 ▲ .
①若,则;
②若,则;
③过空间一点有且只有一条直线与直线成60°角;
④与两条异面直线都垂直的直线有无数条.
9. 与直线切于点,且经过点的圆的方程为 ▲ .
10. 下列命题正确的序号是 ▲ .(其中表示直线,表示平面)
①若;
②若;
③若;
④若.
11. 已知点和点分别在直线的两侧,则实数的取值范围为
▲ .
12. 正方体的棱长为,若过作平面,则截面三角形的面积为 ▲ .
13. 在三棱锥中,侧棱、、两两垂直且长度均为,点在上,且,则的值为 ▲ .
14. 若△ABC的一个顶点,的平分线分别为,则直线BC的方程为 ▲ .
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本题满分14分)
已知直线和.
(1)若和相交于点,求、的值;
(2)若,求、的值;
(3)若点到直线的距离为1,求的值.
16.(本题满分14分)
如图,已知一个圆锥的底面半径为,高为,在其中有一个高为的内接圆柱(其中均为常数).
(1)当时,求内接圆柱上方的圆锥的体积;
(2)当为何值时,这个内接圆柱的侧面积最大?
并求出其最大值。
17.(本题满分14分)
如图已知在三棱柱ABC——A1B1C1中,AA1⊥平面ABC,AC=BC,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.
(1)求证:平面平面;
(2)求证:平面PCC1⊥平面MNQ.
18.(本题满分16分)
如图,直角三角形的顶点坐标,直角顶点,顶点在轴上,点为线段的中点.
(1)求直线BC的斜率及点C的坐标;
(2)求边所在直线方程;
(3)为直角三角形外接圆的圆心,
求圆的方程。
19.(本题满分16分)
如图,在四棱锥中,侧面是正三角形,且与底面垂直,底面是菱形,,是中点,截面交于.
(1)求证:平面;
(2)求证:平面.
20.(本题满分16分)
已知过点的动直线与圆C:相交于P、Q两点,M是PQ中点,与直线相交于点N.
(1)求证:当与垂直时,必过圆心C;
(2)探索是否与直线的倾斜角有关?若无关,请求出其值;若有关,请说明理由.
高二数学(选修历史)参考答案及评分标准
一、填空题
1.假; 2.1个或无数个; 3.120°; 4.6; 5.;
6.; 7.必要不充分; 8.②和④; 9.
10.①、③、④; 11.(-19,-9); 12.; 13.; 14..
二、解答题
15.解:(1)由题意得解得 (4分)
(2)由得或 (10分)
(3)由题意得,解得. (14分)
16.解:圆锥、圆柱的轴截面如图所示,其中
设圆柱底面半径为,则 (3分)
(1)当时,
∴ (8分)
(2)设圆柱的侧面积为.
∵,
∴ (10分)
(12分)
∴当时,. (14分)
17.证明:(1)∵分别是的中点,
∴ (1分)
又∵平面,平面,
∴平面 (4分)
∵平面平面,
∴平面. (5分)
又∵,
∴平面平面. (7分)
(2)∵AC=BC, P是AB的中点,∴AB⊥PC (8分)
∵AA1⊥面ABC,CC1∥AA1,∴CC1⊥面ABC,
而AB在平面ABC内,∴CC1⊥AB, (9分)
∵CC1∩PC=C ∴AB⊥面PCC1; (10分)
又∵M、N分别是AA1、BB1的中点,四边形AA1B1B是平行四边形,MN∥AB,
∴MN⊥面PCC1 (12分)
∵MN在平面MNQ内,∴面PCC1⊥面MNQ; (14分)
18.解:(1)∵,,∴ (3分)
由两点间距离公式得,
由△OAB∽△OBC,得,可求得,
于是在Rt△OBC中可求得,∴ (7分)
(2),由点斜式或两点式可求得.(11分)
(3)在上式中,令,得,∴圆心
又∵,∴外接圆的方程为. (16分)
19.证明:(1),
∴。 (3分)
又∵,,
∴。 (6分)
而,∴ (9分)
(2)取AD中点O,连结BO,BD。
在中,∵,∴ (10分)
在△ABD中,∵AD=AB,,
∴三角形ABD为等边三角形,∴ (11分)
又,,
∴,∴ (14分)
又∵,∴ (16分)
20.解:(1)∵,且,
∴.
故直线的方程为,即 (5分)
∵圆心坐标满足直线的方程,
∴当时,必过圆心C. (7分)
(2)∵,
∴=(9分)
①当轴时,易得,
则 (10分)
又,
∴ (12分)
②当与轴不垂直时,设直线的方程为
,则由得,则 (14分)
∴.
综上所述,与直线的斜率无关,且 (16分)
同课章节目录
