三角形全等的学案
图片预览




文档简介
南县立达中学八年级数学学案 主备人 刘康 同备人:八年级数学组
课题:旋 转 班级 姓名 评价
学习目标 探索旋转的基本性质,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等的性质
学 习 过 程 学习心得
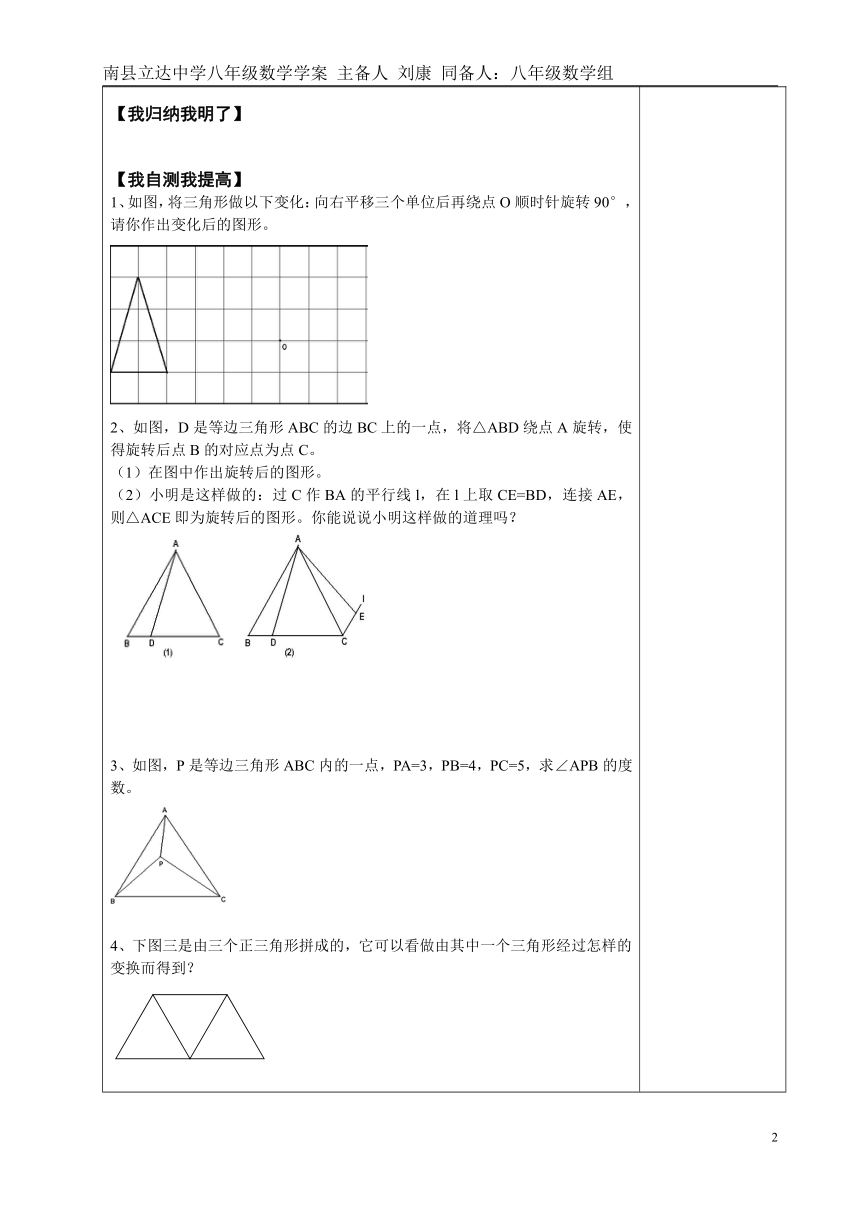
【我预习、我快乐】情景问题,导入课题日常生活中,我们经常见到以下情景(钟表指针的转动、汽车方向盘的转动、辘轳打水的情景等现象)。(1)上面情景中的转动现象,有什么共同特征?(2)钟表的指针、钟摆在转动过程中,其形状、大小、位置是否发生改变?汽车方向盘的转动呢?在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为 (circumrotate)。这个定点称为 ,转动的角称为 。原位置的图形叫 ,新位置的图形叫 ,原位置图形中的点与新位置图形中相对应的点叫 。旋转的基本性质:1、旋转具有不改变图形的大小和形状的特征; 2、任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角彼此相等; 3、对应点到旋转中心的距离相等。【我疑惑、我思考】【我探究、我敢试】1、动手:如下图△ABC绕O点旋转后,顶点A的对应点为点D,试确定顶点B、C对应点的位置,以及旋转后的三角形.2、将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案。3、画出一个正三角形绕它的一个顶点按逆时针方向旋转60°后的图形。【我归纳我明了】【我自测我提高】1、如图,将三角形做以下变化:向右平移三个单位后再绕点O顺时针旋转90°,请你作出变化后的图形。2、如图,D是等边三角形ABC的边BC上的一点,将△ABD绕点A旋转,使得旋转后点B的对应点为点C。(1)在图中作出旋转后的图形。(2)小明是这样做的:过C作BA的平行线l,在l上取CE=BD,连接AE,则△ACE即为旋转后的图形。你能说说小明这样做的道理吗?3、如图,P是等边三角形ABC内的一点,PA=3,PB=4,PC=5,求∠APB的度数。4、下图三是由三个正三角形拼成的,它可以看做由其中一个三角形经过怎样的变换而得到?
课题:图案设计 班级 姓名 评价
学习目标 欣赏图案,掌握图案的设计方法
学 习 过 程 学习心得
【我预习、我会学、我快乐】情景导入欣赏下面的图案回答问题这些美丽的图案有什么特点?怎样设计美丽的图案呢?合作交流,探究新知1 下列图案分别是由哪个基础图形经过怎样的变换画出来的呢? 2 自己来设计,按要求设计A 你设计的图案中要求有一个正方形和一个菱形,且是中心对称图形,又是轴对称图形。B利用下面提供的基本图形,用平移、旋转、轴对称、中心对称等方法进行图案设计,并简要说明自己的设计意图。【我疑惑、我思考】【我探究、我敢试】1、用四块如图所示的瓷砖拼铺成正方形地板,使拼铺的图案成轴对称图形或中心对称图形。2、根据给定基础图形拼图案利用平行四边形和正六边形拼图案,(可以重复使用一个基础图形),并且说明设计意义。如:某同学拼成一部风车。你的设计呢?3 、自由设计,请你先欣赏,再设计如下面的图案,你一定可以设计出更美的图案【我归纳我明了】
课题:旋转的练习课 班级 姓名 评价
学习目标 1、平移的性质,旋转的性质;2、旋转的性质运用。
学 习 过 程 学习心得
【我预习、我会学、我快乐】1、平移改变的是图形的( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2、经过平移,对应点所连的线段 ( )
A 平行 B 相等 C 平行且相等 D 既不平行,又不相等
3、经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同 B 既可能相同也可能不同
C 不同的点移动的距离相同 D 无法确定 小试牛刀,我一定行!1.下列现象中属于旋转的有( )个。地下水位下降;传送带的移动;方向盘的转动;水龙头的开关的转动;钟摆的运动;荡秋千运动A、2 B、3 C、4 D、52、下列现象属于旋转的是( )A、摩托车在急刹车时向前滑动; B飞机起飞后冲向空中的过程。C、转盘转动的过程 ; D、笔直的铁轨上飞驰而过的火车3.△ABC绕着B点旋转后得到△A/BC/。若∠ABC/=130°,∠ABC=80°则旋转角等于( )A、50° B、210° C、50°或120° D、130°4.在图形的旋转中,下列说法错误的是( )A、在图形上的每一点到旋转中心的距离相等; B、在图形上每一点移动的角度相同;C、在图形上可能存在不同的点; D、图形上任意两点的连线与其对应两点的连线长度相等5、如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.6、如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR, (1)指出旋转中心、旋转方向和旋转角度? (2) ACR是否可以直接通过把BQC旋转得到?7.四边形ABCD是边长为了的正方形,且DE=,△ABF是△ADE的旋转图形。问:旋转中心是哪一点?旋转了多少度?AF的长应是多少?连接EF,则AEF是怎样的三角形?【我疑惑、我思考】【我探究、我敢试】题1:将一个已知等边⊿ABC绕A点旋转一定角度后,得到⊿ADE,观察⊿ADE和⊿ABC,回答:⑴线段AB与AD、AC与AE、BC与DE的等量关系?⑵∠BAC与∠DAE的等量关系?⑶⊿ADE和⊿ABC形状大小有什么关系?题2:△ABC绕△ABC外一点 O旋转一定角度的到△A/B/C/线段OA与OA/、OB与OB/、OC与OC/有什么关系?∠AOA/与∠BOB/,∠COC/有什么关系?△ABC与△A/B/C/大小有什么关系?【我归纳我明了】
课题:全等三角形及其性质 班级 姓名 评价
学习目标 1、 全等形和全等三角形的概念及表示法;2 、全等三角形的性质;全等三角形对应边、对应角的确定方法。
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,探究新知观察: 问:(1)我国国徽中四个小五角星能完全重合吗?(2)如果的两幅风景图片是从同一幅图片上复制下来的,能完全重合吗?(3)同一张底片冲洗出来的两种神舟7号飞船照片放在一起能完全重合吗?(4)如上图把三角形ABC绕点A旋转30度得到三角形ADE,三角形ABC与三角形ADE能重合吗? 合作交流、互动探究1 全等形和全等三角形的概念注意:对应点写在对应位置上。考考你:生活中,你还见过哪些全等形,下面图形全等吗 面积相等的两个三角形全等吗?2 全等三角形的性质
【我疑惑、我思考】【我探究、我敢试】做一做:1 把你做的两个三角形顶点标上字母并摆成如图形状,然后按下面要求变换,并指出对应顶点,对应边,对应角,(1)把一个上面△DEF沿着AB边平移(如图2)。(2)把△DEF沿AB 边的垂直平分线作轴反射(如图3); (3)把△DEF绕点A逆时针旋转30度(如图4);(4)把△DEF绕点A逆时针旋转180度(如图5)(5)把△DEF绕AC的重点旋转180度;想一想(1)指出下列全等三角形的对应边和对应角。△ABE与△ACF,△BFO与CEO,△FBC与△ECB(2)找对应边和对应角你有什么经验?【我自测我提高】1 如图,已知△ABE≌△ACD,AB=AC,BE=CD, ∠B=50°,∠AEC=120°,则∠DAC=( )A 120° B 60° C 50° D 70°2 △是由△OAB绕点O逆时针旋转60°得到的,那么△与△OAB是什么关系?若∠AOB=40°,∠B=30°,则∠与是多少度?
课题:全等三角形的判定(一) 班级 姓名 评价
学习目标 1、熟练掌握“边角边”判定的内容,并能应用边角边判定说明两个三角形全等,通过观察几何图形,增强识图能力;2、通过自主学习的发展体验获取数学知识的感受,初步形成勇于创新的精神。
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境(1)画图:问题:已知任意△ABC,画△A1B1C1,使A1B1 = AB,∠B1 = ∠B,B1C1 = BC(2)实验:把所画的△A1B1C1剪下,放在原三角形上,发现什么情况?探究新知,归纳知识全等三角形的判定1: .(简写成“ ”或“ ”).应用格式:已知如图所示在△ABC和△A1B1C1中 = (已知), = (已知), = (已知),所以 ≌ (S.A.S).【我疑惑、我思考】【我探究、我敢试】1 已知线段 BD、A C交于O,如果OA = OD,OB = OC那么△AOB与△DOC全等吗?证明:∵在△AOB与△DOC中 = (已知), = (对顶角相等), = (已知), ∴ ≌ (S.A.S).2 如图,已知AF = CE,AD∥BC,AD = CB,那么△AFD与△CEB全等吗?证明:∵ AD∥BC (已知),∴ = (两直线平行,内错角相等).∴在△AFD与△CEB中 = (已知), = (已求), = (已知),∴ △AFD ≌ △CEB (S.A.S).3 如图,已知A、B、C三点在一条直线上,分别以AB、BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于F,DC交BE于G。求证:AE=DC. 证明:∵△ABD和△BCE为等边⊿,∴ AB= ,BC= ,∠ABD=∠EBC=60°, ∴ = =120°, ∴在△ABE和△DBC中, HYPERLINK "http://" EMBED Equation.3 ∴△ABE≌△DBC(S.A.S.). ∴ = (全等三角形的对应边相等).【我归纳我明了】【我自测我提高】1.如图所示,已知AD∥BC,AD=BC,请你思考一下,△ABC与△CDA有什么关系 ( http: / / )2.如图所示,AB=AC,AD=AE,△ABE与△ACD全等吗 请说明理由.3.如图所示,已知AB∥DC,AB=DC, 求证:AD∥BC. ( http: / / )4.如图所示,M是AB的中点,MC=MD,∠1=∠2.求证:∠C=∠D. 2.在证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形_____来解决.
课题:全等三角形的判定(二) 班级 姓名 评价
学习目标 1、掌握角边角判定、角角边判定的内容;会应用角边角判定及其推论说明两个三角形全等; 2、通过“角边角”和“角角边”判定的运用,提高识图和逻辑思维能力;3、通过几何说明的教学 ( http: / / www. / ),初步养成尊重客观事实和形成质疑的习惯.
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,提出问题问题:一块三角形玻璃碎成如图形状4块,配一块与原来一样的三角形玻璃(1)要不要4块都带去? (2)带哪一块呢?(3)带D块,带去了三角形的几个元素?另外几快呢?探究新知,互动展示判定2在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为“角边角”或“A.S.A”)。问:恢复后的三角形和原三角形全等,那全等的条件是不是就是带去的元素呢?判定3:有两角和其中一角的对边对应相等的两个三角形全等. (简写成“角角边”或“AAS”)【我疑惑、我思考】【我探究、我敢试】1 已知∠BAC=∠DAC,∠BCA=∠DCA,那么△ABC与△ADC全等吗?证明:∵在△ABC与△ADC中= (已知) = (公共边)= (已知)∴ △ABC ≌△ADC (A.S.A)探究:1.想一想:如图,在△ABC与△A’B’C’中,已知∠A=∠A’,∠B=∠B’,AC=A’C’,△ABC与△A’B’C’全等吗?为什么?2已知,M是AB的中点,∠1=∠2,∠C=∠D,问MC=MD吗?说明理由.解:∵ M是AB的中点(已知)∴ = (中点的意义)∴在△AMC与△BMD中= (已知)= (已知) = (已求 )∴ △AMC ≌△BMD (A.A.S)∴ = (全等三角形的对应边相等)【我归纳我明了】【我自测我提高】1、 (1)全等三角形的_________和_________相等;2、如右图,已知AB=DE,∠B=∠DEF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:_____________, 理由是:_____________;这个条件也可以是:_____________, 理由是:_____________;3、已知右图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“ASA”为依据,还缺条件 (2)若以“AAS”为依据,还缺条件 .(3)若以“SAS”为依据,还缺条件 .4、已知△ABC≌△DEF,∠A=70°,∠E=30°,则∠F的度数为 ( )(A) 80° (B) 70° (C) 30° (D) 100°5、在△ABC和△A’B’C’中, AB=A’B’, ∠B=∠B’, 补充条件后仍不一定能保证△ABC≌△A’B’C’, 则补充的这个条件是( ) A.BC=B’C’ B.∠A=∠A’ C.AC=A’C’ D.∠C=∠C’6、如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为 ( )A.15° B.20° C.25° D.30° ( http: / / )7、如果,小强测量河宽AB时,从河岸的A点沿着和AB垂直的方向走到C,并在AC中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D,使D、E、B恰好在一直线上,于是小强说:“CD的长就是河道宽”你能说出这个道理吗?8、如图,已知 AB∥CD,CE∥BF, (1)如果AE=DF,那么BF=CE吗?(2)去掉AE=DF这个条件,请你添一个条件,使得BF=CE成立。
课题:三角形全等的判定(三) 班级 姓名 评价
学习目标 1、掌握已知三边画三角形的方法;掌握边边边判定,能用边边边判定说明两个三角形全等;2、通过判定的初步应用,初步形成逻辑推理能力.
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,提出新知问题:有一块三角形玻璃窗户破碎了,要去配一块新的,你最少要对窗框测量哪几个数据?如果你手头没有测量角度的仪器,只有尺子,你能保证新配的玻璃恰好不大不小吗?探究新知,互动展示问:通过上面问题的分析,满足什么条件的两个三角形全等?全等三角形的判定3:有三边对应相等的两个三角形全等.【我疑惑、我思考】【我探究、我敢试】1、 已知AB = CD,AD = CB,那么△ABD与△CDB全等吗?解:∵在△ABD与△CDB中 = (已知)= (公共边) = (已知)∴ △ABD ≌△CDB (S.S.S)2、 已知,AE = DF,BF = CE,AB = DC,问AB∥DC吗?说明理由.解:∵ = (已知)∴ BF – EF = CE – EF(等式性质)即:BE = CF∴在△ABE与△DCF中 = (已知) = (已求) = (已知)∴ △ABE ≌ △DCF (S.S.S)∴ = (全等三角形的对应角相等)∴ ∥ (内错角相等,两直线平行)【我归纳我明了】【我自测我提高】1、如图,网格中有一个四边形和两个三角形。(1)请你画出三个图形绕点O旋转180°的图形。(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形的对称轴的条数,并求出这个整体图形至少旋转多少度才能与自身重合。2.如图所示,要证明△ACF≌△ BDE,根据给定的条件和指明的依据,将应当添加的条件填在横线上.(1)AC=BD,AC∥BD,__________(A.S.A.);(2)AC=BD,AC∥BD,___________(A.A.S.);(3)CE=DF_________,____________(A.S.A.);(4)AC∥BD,AF∥EB,__________(A.A.S.).3.能够________的两个图形叫做全等形.两个三角形重合时,互相_______的顶点叫做对应顶点.记两个三角形全等时,通常把________顶点的字母写在_____的位置上. 4.如图△ABC≌△ADE,若∠D=∠B,∠C=∠AED 则∠DAE=_________,∠DAB=___________. 5.如图△ABD≌△CDB,若AB=4,AD=5,BD=6,则BC=______,CD=______.6.如图△ABD≌△EBC,AB=3cm,BC=5cm,求DE的长. 5、如图所示,已知AB、CD相交于点O,并且△ACO≌△BDO,CE∥DF.求证:CE=DF.
课题:直角三角形的性质(一) 班级 姓名 评价
学习目标 1、掌握“直角三角形的两个锐角互余”定理。2、巩固利用添辅助线证明有关几何问题的方法。
学 习 过 程 学习心得
【我预习、我会学、我快乐】合作交流互动展示1 什么叫直角三角形?2 直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质 3 看图形:∠A与∠B有何关系?为什么?4 归纳小结:直角三角形的性质定理1:直角三角形的 。5 实验操作: 已知直角三角形ABC的纸片,∠ACB=90°(l)量一量斜边AB的长度 (2)找到斜边的中点,用字母D表示 (3)画出斜边上的中线 (4)量一量斜边上的中线的长度 猜想斜边上的中线与斜边长度之间有何关系?归纳小结:直角三角形的性质定理2:直角三角形中,斜边上的中线 斜边的 。【我疑惑、我思考】【我探究、我敢试】(1)在直角三角形中,有一个锐角为52°,那么另一个锐角度数 (2)在Rt△ABC中,∠C=90°,∠A -∠B =30°,那么∠A= ,∠B= 。(3) 如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,那么,(1)与∠B互余的角有 (2)与∠A相等的角有 。(3)与∠B相等的角有 。(4)在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有_________,与∠A相等的角有_________,若∠A=35°,那么∠ECB= _________。【我归纳我明了】【我自测我提高】1 已知:∠ABC=∠ADC=90°,E是AC中点。求证:(1)ED=EB (2)∠EBD=∠EDB 2 如图,已知⊿ABC和⊿ADC都是直角三角形,∠ABC=90°,∠ADC=90°,点E是线段AC的中点,则下图中有哪些等腰三角形?并说明理由 3 已知:在△ABC中,BD、CE分别是边AC、AB上的高, M是BC的中点。如果连接DE,取DE的中点 O,那么MO 与DE有什么样的关系存在
课题:直角三角形的性质(二) 班级 姓名 评价
学习目标 1、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用。2、巩固利用添辅助线证明有关几何问题的方法。3、通过图形的变换,引导学生发现并提出新问题,进行类比联想,促进学生的思维向多层次多方位发散。培养学生的创新精神和创造能力。
学 习 过 程 学习心得
【我预习、我会学、我快乐】【情景导入、激发兴趣】如果你是设计师: 2011年益阳将建造一个地铁站,设计师设想把地铁站的出口建造在离附近的三个公交站点45路、13路、23路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。你会把地铁站的出口建造在哪里?说说你的设计理由【合作交流互动展示】已知:如图,在△ABC中,∠B=∠C,AD是∠BAC的平分线,E、F分别AB、AC的中点。求证:DE=DF 命题:直角三角形斜边上的中线等于斜边的一半【我疑惑、我思考】【我探究、我敢试】已知:在△ABC中,BD、CE分别是边AC、AB上的高,F是BC的中点。求证:FD=FE练习引申:(1)若连接DE,能得出什么结论?说明理由(2)若O是DE的中点,则MO与DE存在什么结论吗?说明理由【我归纳我明了】【我自测我提高】1、如果两个直角三角形共用一条斜边,两个直角三角形位于斜边的同侧。如果共用一条斜边,两个直角三角形位于斜边的两侧我们又会有哪些结论? 试说明理由2、已知:∠ABC=∠ADC=90 ,E是AC中点。你能得到什么结论?并说明理由
课题:直角三角形全等判定定理 班级 姓名 评价
学习目标 1.理解判定两个直角三角形全等可用已经学过的全等三角形判定方法来判定;2.掌握“HL”公理,并能熟练地利用和一般三角形全等的判定方法来判定两个直角三角形全等.
学 习 过 程 学习心得
【我预习、我会学、我快乐】【情景导入、激发兴趣】复习提问1.三角形全等的判定方法有哪几种?2.三角形按角的分类为3.如图3-43,在△ABC与△A'B'C'中,若AB=A'B',AC=△A'C',∠C=∠C'=Rt∠,这时Rt△ABC与Rt△A'B'C'是否全等?斜边、直角边公理:有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).【我疑惑、我思考】【我探究、我敢试】1具有下列条件的Rt△ABC与Rt△A'B'C'(其中∠C=∠C'=Rt∠)是否全等?如果全等在( )里填写理由,如果不全等在( )里打“×”.(1)AC=A'C',∠A=∠A' ( )(2)AC=A'C', BC=B'C' ( )(3)∠A=∠A',∠B=∠B' ( )(4) AB=A'B',∠B=∠B' ( )(5) AC=A'C', AB=A'B' ( )2.如图3-46,已知∠ACB=∠BDA=Rt∠,若要使△ACB ≌△BDA,还需要什么条件?把它们分别写出来(有几种不同的方法就写几种). INCLUDEPICTURE "http://192.168.0.45:8080/Resource/CZ/CZSX/JAJC/CEJH/tbjxd220ZW_0010_4.gif" \* MERGEFORMATINET 理由:( )( )( )( )3.已知在△ABC和△A'B'C'中,CD、C'D'分别是高,并且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.求证:△ABC≌△A'B'C'.【我归纳我明了】【我自测我提高】1、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?2、如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。【我反思我颖悟】
课题:直角三角形全等 班级 姓名 评价
学习目标 1、探索两个直角三角形全等的条件 ;2、掌握两个直角三角形全等的条件(HL):斜边和一条直角边对应相等的两个直角三角形全等 ;3、了解角平分线的性质:角的内部,到角两边距离相等的点,在这个角的平分线上,在这个角的平分线上,及其简单应用
学 习 过 程 学习心得
【我预习、我会学、我快乐】【合作探究,共同展示】1.判断满足下列条件的两个直角三角形是否全等.若全等,画“√”号;若不全等,画“×”号. (1)一个锐角和这个锐角的对边对应相等. ( ) (2)一个锐角和锐角相邻的直角边对应相等. ( ) (3)一个锐角和一条斜边对应相等. ( ) (4)两直角边对应相等. ( ) (5)两锐角对应相等. ( )2.如图所示,要证明△ACF≌△ BDE,根据给定的条件和指明的依据,将应当添加的条件填在横线上.(1)AC=BD,AC∥BD,__________(A.S.A.);(2)AC=BD,AC∥BD,___________(A.A.S.);(3)CE=DF_________,____________(A.S.A.);(4)AC∥BD,AF∥EB,__________(A.A.S.).【我疑惑、我思考】【我探究、我敢试】1.如图所示,已知AB、CD相交于点O,并且△ACO≌△BDO,CE∥DF.求证:CE=DF. 2.如图所示,已知∠1=∠2,∠ 3=∠4.求证:AB=AC. ( http: / / )3.如图所示,已知AB∥DC,AB=CD,BF=DE.求证:AE∥CF,AF∥CE. ( http: / / )【我归纳我明了】【我自测我提高】1.如图所示,已知EF⊥AD于E,CB⊥AD于B,EF=BC,AE=BD.求证:∠C=∠F. 2.如图所示,△ABC是等腰直角三角形,即AC=BC,∠BAC=∠B=45°,∠ACB=90°.AD是BC边上的中线,过C作AD的垂线,交AB于点E.交AD于点F,试判断∠ADC与∠BDE的大小关系. ( http: / / )
O
D
C
B
A
B
C
P
R
A
A
D
C
B
F
E
A
B
C
B1
C1
A1
A
B
C
D
E
F
D
B
C
A
M
A
B
C
D
1
2
F
C
D
B
A
E
A
B
C
D
E
F
A
C
B
A
C
B
D
PAGE
22
课题:旋 转 班级 姓名 评价
学习目标 探索旋转的基本性质,理解旋转前后两个图形对应点到旋转中心的距离相等,对应点与旋转中心的连线所成的角彼此相等的性质
学 习 过 程 学习心得
【我预习、我快乐】情景问题,导入课题日常生活中,我们经常见到以下情景(钟表指针的转动、汽车方向盘的转动、辘轳打水的情景等现象)。(1)上面情景中的转动现象,有什么共同特征?(2)钟表的指针、钟摆在转动过程中,其形状、大小、位置是否发生改变?汽车方向盘的转动呢?在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,这样的图形运动称为 (circumrotate)。这个定点称为 ,转动的角称为 。原位置的图形叫 ,新位置的图形叫 ,原位置图形中的点与新位置图形中相对应的点叫 。旋转的基本性质:1、旋转具有不改变图形的大小和形状的特征; 2、任意一对对应点与旋转中心的连线所成的角都是旋转角,旋转角彼此相等; 3、对应点到旋转中心的距离相等。【我疑惑、我思考】【我探究、我敢试】1、动手:如下图△ABC绕O点旋转后,顶点A的对应点为点D,试确定顶点B、C对应点的位置,以及旋转后的三角形.2、将下图中大写字母N绕它右下侧的顶点按顺时针方向旋转90 ,作出旋转后的图案。3、画出一个正三角形绕它的一个顶点按逆时针方向旋转60°后的图形。【我归纳我明了】【我自测我提高】1、如图,将三角形做以下变化:向右平移三个单位后再绕点O顺时针旋转90°,请你作出变化后的图形。2、如图,D是等边三角形ABC的边BC上的一点,将△ABD绕点A旋转,使得旋转后点B的对应点为点C。(1)在图中作出旋转后的图形。(2)小明是这样做的:过C作BA的平行线l,在l上取CE=BD,连接AE,则△ACE即为旋转后的图形。你能说说小明这样做的道理吗?3、如图,P是等边三角形ABC内的一点,PA=3,PB=4,PC=5,求∠APB的度数。4、下图三是由三个正三角形拼成的,它可以看做由其中一个三角形经过怎样的变换而得到?
课题:图案设计 班级 姓名 评价
学习目标 欣赏图案,掌握图案的设计方法
学 习 过 程 学习心得
【我预习、我会学、我快乐】情景导入欣赏下面的图案回答问题这些美丽的图案有什么特点?怎样设计美丽的图案呢?合作交流,探究新知1 下列图案分别是由哪个基础图形经过怎样的变换画出来的呢? 2 自己来设计,按要求设计A 你设计的图案中要求有一个正方形和一个菱形,且是中心对称图形,又是轴对称图形。B利用下面提供的基本图形,用平移、旋转、轴对称、中心对称等方法进行图案设计,并简要说明自己的设计意图。【我疑惑、我思考】【我探究、我敢试】1、用四块如图所示的瓷砖拼铺成正方形地板,使拼铺的图案成轴对称图形或中心对称图形。2、根据给定基础图形拼图案利用平行四边形和正六边形拼图案,(可以重复使用一个基础图形),并且说明设计意义。如:某同学拼成一部风车。你的设计呢?3 、自由设计,请你先欣赏,再设计如下面的图案,你一定可以设计出更美的图案【我归纳我明了】
课题:旋转的练习课 班级 姓名 评价
学习目标 1、平移的性质,旋转的性质;2、旋转的性质运用。
学 习 过 程 学习心得
【我预习、我会学、我快乐】1、平移改变的是图形的( )
A 位置 B 大小 C 形状 D 位置、大小和形状
2、经过平移,对应点所连的线段 ( )
A 平行 B 相等 C 平行且相等 D 既不平行,又不相等
3、经过平移,图形上每个点都沿同一个方向移动了一段距离下面说法正确的是 ( )
A 不同的点移动的距离不同 B 既可能相同也可能不同
C 不同的点移动的距离相同 D 无法确定 小试牛刀,我一定行!1.下列现象中属于旋转的有( )个。地下水位下降;传送带的移动;方向盘的转动;水龙头的开关的转动;钟摆的运动;荡秋千运动A、2 B、3 C、4 D、52、下列现象属于旋转的是( )A、摩托车在急刹车时向前滑动; B飞机起飞后冲向空中的过程。C、转盘转动的过程 ; D、笔直的铁轨上飞驰而过的火车3.△ABC绕着B点旋转后得到△A/BC/。若∠ABC/=130°,∠ABC=80°则旋转角等于( )A、50° B、210° C、50°或120° D、130°4.在图形的旋转中,下列说法错误的是( )A、在图形上的每一点到旋转中心的距离相等; B、在图形上每一点移动的角度相同;C、在图形上可能存在不同的点; D、图形上任意两点的连线与其对应两点的连线长度相等5、如图,△ABC为等边三角形,D是△ABC内一点,若将△ABD经过旋转后到△ACP位置,则旋转中心是__________,旋转角等于_________度,△ADP是___________三角形.6、如图:P是等边ABC内的一点,把ABP按不同的方向通过旋转得到BQC和ACR, (1)指出旋转中心、旋转方向和旋转角度? (2) ACR是否可以直接通过把BQC旋转得到?7.四边形ABCD是边长为了的正方形,且DE=,△ABF是△ADE的旋转图形。问:旋转中心是哪一点?旋转了多少度?AF的长应是多少?连接EF,则AEF是怎样的三角形?【我疑惑、我思考】【我探究、我敢试】题1:将一个已知等边⊿ABC绕A点旋转一定角度后,得到⊿ADE,观察⊿ADE和⊿ABC,回答:⑴线段AB与AD、AC与AE、BC与DE的等量关系?⑵∠BAC与∠DAE的等量关系?⑶⊿ADE和⊿ABC形状大小有什么关系?题2:△ABC绕△ABC外一点 O旋转一定角度的到△A/B/C/线段OA与OA/、OB与OB/、OC与OC/有什么关系?∠AOA/与∠BOB/,∠COC/有什么关系?△ABC与△A/B/C/大小有什么关系?【我归纳我明了】
课题:全等三角形及其性质 班级 姓名 评价
学习目标 1、 全等形和全等三角形的概念及表示法;2 、全等三角形的性质;全等三角形对应边、对应角的确定方法。
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,探究新知观察: 问:(1)我国国徽中四个小五角星能完全重合吗?(2)如果的两幅风景图片是从同一幅图片上复制下来的,能完全重合吗?(3)同一张底片冲洗出来的两种神舟7号飞船照片放在一起能完全重合吗?(4)如上图把三角形ABC绕点A旋转30度得到三角形ADE,三角形ABC与三角形ADE能重合吗? 合作交流、互动探究1 全等形和全等三角形的概念注意:对应点写在对应位置上。考考你:生活中,你还见过哪些全等形,下面图形全等吗 面积相等的两个三角形全等吗?2 全等三角形的性质
【我疑惑、我思考】【我探究、我敢试】做一做:1 把你做的两个三角形顶点标上字母并摆成如图形状,然后按下面要求变换,并指出对应顶点,对应边,对应角,(1)把一个上面△DEF沿着AB边平移(如图2)。(2)把△DEF沿AB 边的垂直平分线作轴反射(如图3); (3)把△DEF绕点A逆时针旋转30度(如图4);(4)把△DEF绕点A逆时针旋转180度(如图5)(5)把△DEF绕AC的重点旋转180度;想一想(1)指出下列全等三角形的对应边和对应角。△ABE与△ACF,△BFO与CEO,△FBC与△ECB(2)找对应边和对应角你有什么经验?【我自测我提高】1 如图,已知△ABE≌△ACD,AB=AC,BE=CD, ∠B=50°,∠AEC=120°,则∠DAC=( )A 120° B 60° C 50° D 70°2 △是由△OAB绕点O逆时针旋转60°得到的,那么△与△OAB是什么关系?若∠AOB=40°,∠B=30°,则∠与是多少度?
课题:全等三角形的判定(一) 班级 姓名 评价
学习目标 1、熟练掌握“边角边”判定的内容,并能应用边角边判定说明两个三角形全等,通过观察几何图形,增强识图能力;2、通过自主学习的发展体验获取数学知识的感受,初步形成勇于创新的精神。
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境(1)画图:问题:已知任意△ABC,画△A1B1C1,使A1B1 = AB,∠B1 = ∠B,B1C1 = BC(2)实验:把所画的△A1B1C1剪下,放在原三角形上,发现什么情况?探究新知,归纳知识全等三角形的判定1: .(简写成“ ”或“ ”).应用格式:已知如图所示在△ABC和△A1B1C1中 = (已知), = (已知), = (已知),所以 ≌ (S.A.S).【我疑惑、我思考】【我探究、我敢试】1 已知线段 BD、A C交于O,如果OA = OD,OB = OC那么△AOB与△DOC全等吗?证明:∵在△AOB与△DOC中 = (已知), = (对顶角相等), = (已知), ∴ ≌ (S.A.S).2 如图,已知AF = CE,AD∥BC,AD = CB,那么△AFD与△CEB全等吗?证明:∵ AD∥BC (已知),∴ = (两直线平行,内错角相等).∴在△AFD与△CEB中 = (已知), = (已求), = (已知),∴ △AFD ≌ △CEB (S.A.S).3 如图,已知A、B、C三点在一条直线上,分别以AB、BC为边在AC同侧作等边⊿ABD和等边⊿BCE,AE交BD于F,DC交BE于G。求证:AE=DC. 证明:∵△ABD和△BCE为等边⊿,∴ AB= ,BC= ,∠ABD=∠EBC=60°, ∴ = =120°, ∴在△ABE和△DBC中, HYPERLINK "http://" EMBED Equation.3 ∴△ABE≌△DBC(S.A.S.). ∴ = (全等三角形的对应边相等).【我归纳我明了】【我自测我提高】1.如图所示,已知AD∥BC,AD=BC,请你思考一下,△ABC与△CDA有什么关系 ( http: / / )2.如图所示,AB=AC,AD=AE,△ABE与△ACD全等吗 请说明理由.3.如图所示,已知AB∥DC,AB=DC, 求证:AD∥BC. ( http: / / )4.如图所示,M是AB的中点,MC=MD,∠1=∠2.求证:∠C=∠D. 2.在证明分别属于两个三角形的线段相等或角相等的问题,常常通过证明这两个三角形_____来解决.
课题:全等三角形的判定(二) 班级 姓名 评价
学习目标 1、掌握角边角判定、角角边判定的内容;会应用角边角判定及其推论说明两个三角形全等; 2、通过“角边角”和“角角边”判定的运用,提高识图和逻辑思维能力;3、通过几何说明的教学 ( http: / / www. / ),初步养成尊重客观事实和形成质疑的习惯.
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,提出问题问题:一块三角形玻璃碎成如图形状4块,配一块与原来一样的三角形玻璃(1)要不要4块都带去? (2)带哪一块呢?(3)带D块,带去了三角形的几个元素?另外几快呢?探究新知,互动展示判定2在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为“角边角”或“A.S.A”)。问:恢复后的三角形和原三角形全等,那全等的条件是不是就是带去的元素呢?判定3:有两角和其中一角的对边对应相等的两个三角形全等. (简写成“角角边”或“AAS”)【我疑惑、我思考】【我探究、我敢试】1 已知∠BAC=∠DAC,∠BCA=∠DCA,那么△ABC与△ADC全等吗?证明:∵在△ABC与△ADC中= (已知) = (公共边)= (已知)∴ △ABC ≌△ADC (A.S.A)探究:1.想一想:如图,在△ABC与△A’B’C’中,已知∠A=∠A’,∠B=∠B’,AC=A’C’,△ABC与△A’B’C’全等吗?为什么?2已知,M是AB的中点,∠1=∠2,∠C=∠D,问MC=MD吗?说明理由.解:∵ M是AB的中点(已知)∴ = (中点的意义)∴在△AMC与△BMD中= (已知)= (已知) = (已求 )∴ △AMC ≌△BMD (A.A.S)∴ = (全等三角形的对应边相等)【我归纳我明了】【我自测我提高】1、 (1)全等三角形的_________和_________相等;2、如右图,已知AB=DE,∠B=∠DEF,若要使△ABC≌△DEF,那么还要需要一个条件,这个条件可以是:_____________, 理由是:_____________;这个条件也可以是:_____________, 理由是:_____________;3、已知右图,∠B=∠DEF,AB=DE,要说明△ABC≌△DEF,(1)若以“ASA”为依据,还缺条件 (2)若以“AAS”为依据,还缺条件 .(3)若以“SAS”为依据,还缺条件 .4、已知△ABC≌△DEF,∠A=70°,∠E=30°,则∠F的度数为 ( )(A) 80° (B) 70° (C) 30° (D) 100°5、在△ABC和△A’B’C’中, AB=A’B’, ∠B=∠B’, 补充条件后仍不一定能保证△ABC≌△A’B’C’, 则补充的这个条件是( ) A.BC=B’C’ B.∠A=∠A’ C.AC=A’C’ D.∠C=∠C’6、如图,在△ABC中,D、E分别是边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为 ( )A.15° B.20° C.25° D.30° ( http: / / )7、如果,小强测量河宽AB时,从河岸的A点沿着和AB垂直的方向走到C,并在AC中点E处立一根标杆,然后从C点沿着和AC垂直的方向走到D,使D、E、B恰好在一直线上,于是小强说:“CD的长就是河道宽”你能说出这个道理吗?8、如图,已知 AB∥CD,CE∥BF, (1)如果AE=DF,那么BF=CE吗?(2)去掉AE=DF这个条件,请你添一个条件,使得BF=CE成立。
课题:三角形全等的判定(三) 班级 姓名 评价
学习目标 1、掌握已知三边画三角形的方法;掌握边边边判定,能用边边边判定说明两个三角形全等;2、通过判定的初步应用,初步形成逻辑推理能力.
学 习 过 程 学习心得
【我预习、我会学、我快乐】创设情境,提出新知问题:有一块三角形玻璃窗户破碎了,要去配一块新的,你最少要对窗框测量哪几个数据?如果你手头没有测量角度的仪器,只有尺子,你能保证新配的玻璃恰好不大不小吗?探究新知,互动展示问:通过上面问题的分析,满足什么条件的两个三角形全等?全等三角形的判定3:有三边对应相等的两个三角形全等.【我疑惑、我思考】【我探究、我敢试】1、 已知AB = CD,AD = CB,那么△ABD与△CDB全等吗?解:∵在△ABD与△CDB中 = (已知)= (公共边) = (已知)∴ △ABD ≌△CDB (S.S.S)2、 已知,AE = DF,BF = CE,AB = DC,问AB∥DC吗?说明理由.解:∵ = (已知)∴ BF – EF = CE – EF(等式性质)即:BE = CF∴在△ABE与△DCF中 = (已知) = (已求) = (已知)∴ △ABE ≌ △DCF (S.S.S)∴ = (全等三角形的对应角相等)∴ ∥ (内错角相等,两直线平行)【我归纳我明了】【我自测我提高】1、如图,网格中有一个四边形和两个三角形。(1)请你画出三个图形绕点O旋转180°的图形。(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形的对称轴的条数,并求出这个整体图形至少旋转多少度才能与自身重合。2.如图所示,要证明△ACF≌△ BDE,根据给定的条件和指明的依据,将应当添加的条件填在横线上.(1)AC=BD,AC∥BD,__________(A.S.A.);(2)AC=BD,AC∥BD,___________(A.A.S.);(3)CE=DF_________,____________(A.S.A.);(4)AC∥BD,AF∥EB,__________(A.A.S.).3.能够________的两个图形叫做全等形.两个三角形重合时,互相_______的顶点叫做对应顶点.记两个三角形全等时,通常把________顶点的字母写在_____的位置上. 4.如图△ABC≌△ADE,若∠D=∠B,∠C=∠AED 则∠DAE=_________,∠DAB=___________. 5.如图△ABD≌△CDB,若AB=4,AD=5,BD=6,则BC=______,CD=______.6.如图△ABD≌△EBC,AB=3cm,BC=5cm,求DE的长. 5、如图所示,已知AB、CD相交于点O,并且△ACO≌△BDO,CE∥DF.求证:CE=DF.
课题:直角三角形的性质(一) 班级 姓名 评价
学习目标 1、掌握“直角三角形的两个锐角互余”定理。2、巩固利用添辅助线证明有关几何问题的方法。
学 习 过 程 学习心得
【我预习、我会学、我快乐】合作交流互动展示1 什么叫直角三角形?2 直角三角形是一类特殊的三角形,除了具备三角形的性质外,还具备哪些性质 3 看图形:∠A与∠B有何关系?为什么?4 归纳小结:直角三角形的性质定理1:直角三角形的 。5 实验操作: 已知直角三角形ABC的纸片,∠ACB=90°(l)量一量斜边AB的长度 (2)找到斜边的中点,用字母D表示 (3)画出斜边上的中线 (4)量一量斜边上的中线的长度 猜想斜边上的中线与斜边长度之间有何关系?归纳小结:直角三角形的性质定理2:直角三角形中,斜边上的中线 斜边的 。【我疑惑、我思考】【我探究、我敢试】(1)在直角三角形中,有一个锐角为52°,那么另一个锐角度数 (2)在Rt△ABC中,∠C=90°,∠A -∠B =30°,那么∠A= ,∠B= 。(3) 如图,在△ABC中,∠ACB=90°,CD是斜边AB上的高,那么,(1)与∠B互余的角有 (2)与∠A相等的角有 。(3)与∠B相等的角有 。(4)在△ABC中, ∠ACB=90 °,CE是AB边上的中线,那么与CE相等的线段有_________,与∠A相等的角有_________,若∠A=35°,那么∠ECB= _________。【我归纳我明了】【我自测我提高】1 已知:∠ABC=∠ADC=90°,E是AC中点。求证:(1)ED=EB (2)∠EBD=∠EDB 2 如图,已知⊿ABC和⊿ADC都是直角三角形,∠ABC=90°,∠ADC=90°,点E是线段AC的中点,则下图中有哪些等腰三角形?并说明理由 3 已知:在△ABC中,BD、CE分别是边AC、AB上的高, M是BC的中点。如果连接DE,取DE的中点 O,那么MO 与DE有什么样的关系存在
课题:直角三角形的性质(二) 班级 姓名 评价
学习目标 1、掌握“直角三角形斜边上的中线等于斜边的一半”定理以及应用。2、巩固利用添辅助线证明有关几何问题的方法。3、通过图形的变换,引导学生发现并提出新问题,进行类比联想,促进学生的思维向多层次多方位发散。培养学生的创新精神和创造能力。
学 习 过 程 学习心得
【我预习、我会学、我快乐】【情景导入、激发兴趣】如果你是设计师: 2011年益阳将建造一个地铁站,设计师设想把地铁站的出口建造在离附近的三个公交站点45路、13路、23路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。你会把地铁站的出口建造在哪里?说说你的设计理由【合作交流互动展示】已知:如图,在△ABC中,∠B=∠C,AD是∠BAC的平分线,E、F分别AB、AC的中点。求证:DE=DF 命题:直角三角形斜边上的中线等于斜边的一半【我疑惑、我思考】【我探究、我敢试】已知:在△ABC中,BD、CE分别是边AC、AB上的高,F是BC的中点。求证:FD=FE练习引申:(1)若连接DE,能得出什么结论?说明理由(2)若O是DE的中点,则MO与DE存在什么结论吗?说明理由【我归纳我明了】【我自测我提高】1、如果两个直角三角形共用一条斜边,两个直角三角形位于斜边的同侧。如果共用一条斜边,两个直角三角形位于斜边的两侧我们又会有哪些结论? 试说明理由2、已知:∠ABC=∠ADC=90 ,E是AC中点。你能得到什么结论?并说明理由
课题:直角三角形全等判定定理 班级 姓名 评价
学习目标 1.理解判定两个直角三角形全等可用已经学过的全等三角形判定方法来判定;2.掌握“HL”公理,并能熟练地利用和一般三角形全等的判定方法来判定两个直角三角形全等.
学 习 过 程 学习心得
【我预习、我会学、我快乐】【情景导入、激发兴趣】复习提问1.三角形全等的判定方法有哪几种?2.三角形按角的分类为3.如图3-43,在△ABC与△A'B'C'中,若AB=A'B',AC=△A'C',∠C=∠C'=Rt∠,这时Rt△ABC与Rt△A'B'C'是否全等?斜边、直角边公理:有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).【我疑惑、我思考】【我探究、我敢试】1具有下列条件的Rt△ABC与Rt△A'B'C'(其中∠C=∠C'=Rt∠)是否全等?如果全等在( )里填写理由,如果不全等在( )里打“×”.(1)AC=A'C',∠A=∠A' ( )(2)AC=A'C', BC=B'C' ( )(3)∠A=∠A',∠B=∠B' ( )(4) AB=A'B',∠B=∠B' ( )(5) AC=A'C', AB=A'B' ( )2.如图3-46,已知∠ACB=∠BDA=Rt∠,若要使△ACB ≌△BDA,还需要什么条件?把它们分别写出来(有几种不同的方法就写几种). INCLUDEPICTURE "http://192.168.0.45:8080/Resource/CZ/CZSX/JAJC/CEJH/tbjxd220ZW_0010_4.gif" \* MERGEFORMATINET 理由:( )( )( )( )3.已知在△ABC和△A'B'C'中,CD、C'D'分别是高,并且AC=A'C',CD=C'D',∠ACB=∠A'C'B'.求证:△ABC≌△A'B'C'.【我归纳我明了】【我自测我提高】1、如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?2、如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。【我反思我颖悟】
课题:直角三角形全等 班级 姓名 评价
学习目标 1、探索两个直角三角形全等的条件 ;2、掌握两个直角三角形全等的条件(HL):斜边和一条直角边对应相等的两个直角三角形全等 ;3、了解角平分线的性质:角的内部,到角两边距离相等的点,在这个角的平分线上,在这个角的平分线上,及其简单应用
学 习 过 程 学习心得
【我预习、我会学、我快乐】【合作探究,共同展示】1.判断满足下列条件的两个直角三角形是否全等.若全等,画“√”号;若不全等,画“×”号. (1)一个锐角和这个锐角的对边对应相等. ( ) (2)一个锐角和锐角相邻的直角边对应相等. ( ) (3)一个锐角和一条斜边对应相等. ( ) (4)两直角边对应相等. ( ) (5)两锐角对应相等. ( )2.如图所示,要证明△ACF≌△ BDE,根据给定的条件和指明的依据,将应当添加的条件填在横线上.(1)AC=BD,AC∥BD,__________(A.S.A.);(2)AC=BD,AC∥BD,___________(A.A.S.);(3)CE=DF_________,____________(A.S.A.);(4)AC∥BD,AF∥EB,__________(A.A.S.).【我疑惑、我思考】【我探究、我敢试】1.如图所示,已知AB、CD相交于点O,并且△ACO≌△BDO,CE∥DF.求证:CE=DF. 2.如图所示,已知∠1=∠2,∠ 3=∠4.求证:AB=AC. ( http: / / )3.如图所示,已知AB∥DC,AB=CD,BF=DE.求证:AE∥CF,AF∥CE. ( http: / / )【我归纳我明了】【我自测我提高】1.如图所示,已知EF⊥AD于E,CB⊥AD于B,EF=BC,AE=BD.求证:∠C=∠F. 2.如图所示,△ABC是等腰直角三角形,即AC=BC,∠BAC=∠B=45°,∠ACB=90°.AD是BC边上的中线,过C作AD的垂线,交AB于点E.交AD于点F,试判断∠ADC与∠BDE的大小关系. ( http: / / )
O
D
C
B
A
B
C
P
R
A
A
D
C
B
F
E
A
B
C
B1
C1
A1
A
B
C
D
E
F
D
B
C
A
M
A
B
C
D
1
2
F
C
D
B
A
E
A
B
C
D
E
F
A
C
B
A
C
B
D
PAGE
22
同课章节目录
