多项式乘法
图片预览




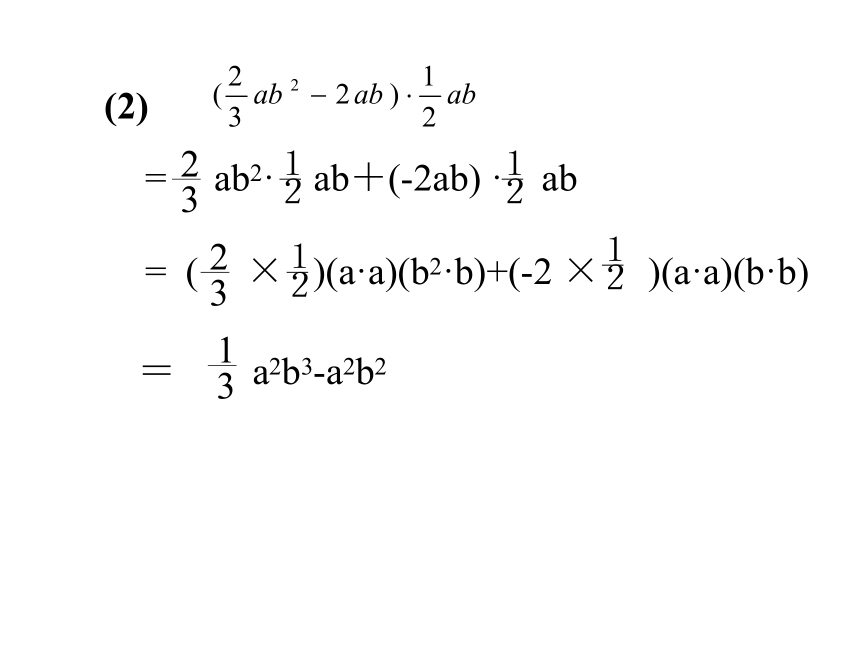


文档简介
课件22张PPT。多项式乘以多项式课前练习(1)(-x)3·(-x)3·(-x)5=______;
(2) (x2)4=_______;
(3) (x3y5)4=______;
(4) (-3x3y)(-5x4y2z4)=_______;-x11x8x12y2015x7y3z4问题:三家连锁店以相同的价格m(单位:元/瓶)销售某种商品,它们在一个月内的销售量(单位:瓶)分别是a,b,c你能用不同的方法计算它们在这个月内销售这种商品的总收入吗?由于①②均表示总收入,所以:m﹙a+b+c﹚=ma+mb+mc单项式与多项式相乘,就是用单项式去乘多项式的每一项,把所得的积相加。 m﹙a+b+c﹚mambmc﹙a+b+c﹚解:(1) (-4x2). (3x+1)
= (-4x2). (3x)+ (-4x2)·1
=(-4×3).(x2. x)+(-4x2)
=-12x3 -4x2 (2)
练习:1、计算
(1)3a(5a-2b) (2)(x-3y)(-6x)
2、化简:x(x-1)+2x(x+1)-3x(2x-5)答案:1、(1)15a2-6ab (2)-6x2+18yx
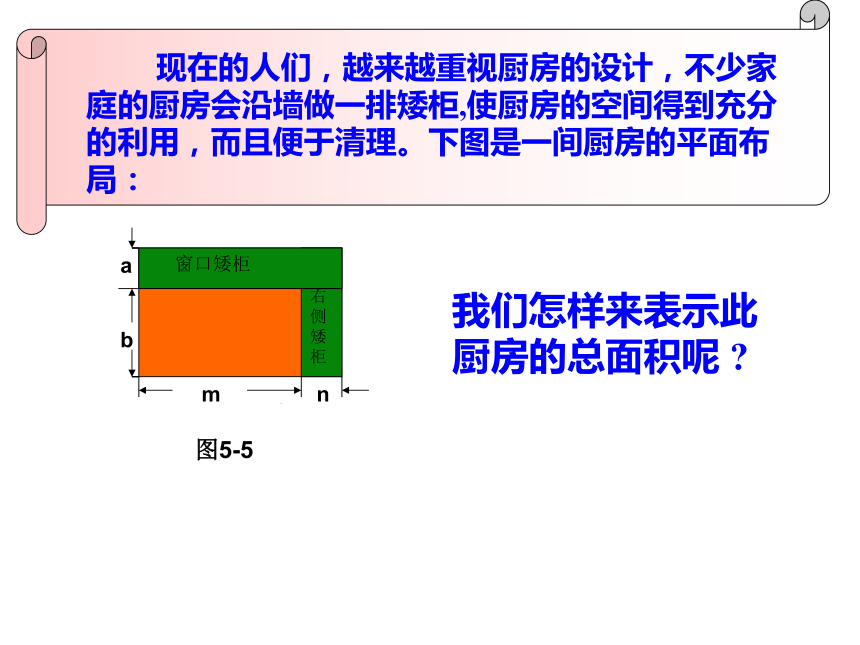
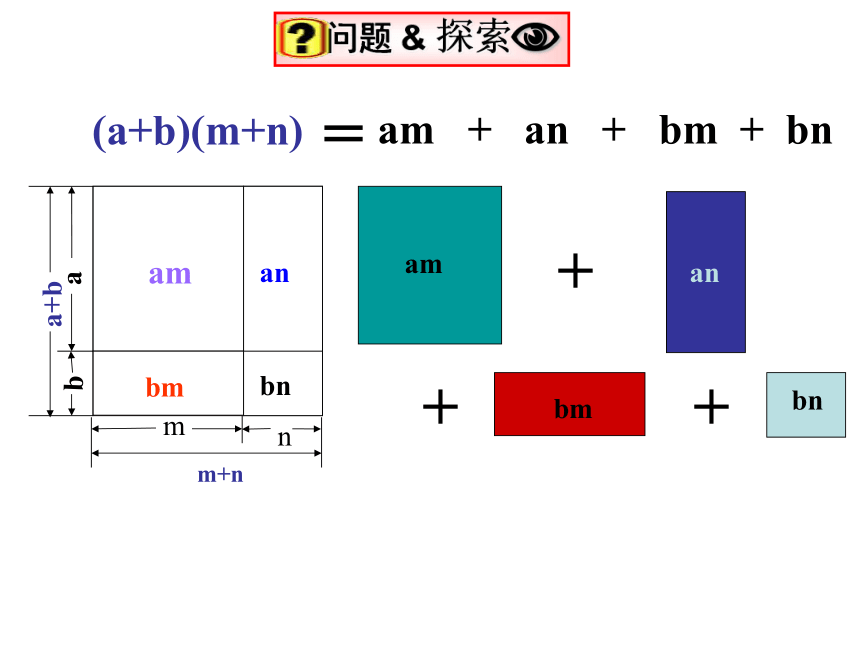
2、-3x2+16xb窗口矮柜右侧矮柜mn图5-5a我们怎样来表示此厨房的总面积呢 ?a+bm+nabambmmab窗口矮柜右侧矮柜mn图5-5图5-6图5-7由图5-6,可得总面积为 (a+b)(m+n);由图5-7,可得总面积为 a(m+n)+b(m+n) 或 am+an+bm+nn.anbnna(1) (2) (3) anbm a+babanbmam + an + bm + bn=+++(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:(1) (x+2y)(5a+3b) ;(2) (2x–3)(x+4) ;解:(x+2y)(5a+3b) ==解:(2x–3)(x+4)2x2 +8x –3x –12=2x2 +5x例1 计算:=–12x ·5a +x ·3b +2y ·5a +2y ·3b5ax+3bx+10ay+6by 练习一、计算:(1) (2n+6)(n–3);(2) (2x+3)(3x–1);例2,先化简,再求值:
(2a-3)(3a+1)-6a(a-4),其中a=解:原式=17a-3,则当a=
17a-3=1练习二、计算: 1、漏乘 需要注意的几个问题2、符号问题 3、最后结果应化成最简形式。判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由。解:原式延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:学了这节课,你有什么收获? 说一说:小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式想乘的展开式中,有同类项要合并同类项. 能力拓展若(x3+mx+n)(x2-5x+3)展开后不含x3和x2项,试求m,n的值.
(2) (x2)4=_______;
(3) (x3y5)4=______;
(4) (-3x3y)(-5x4y2z4)=_______;-x11x8x12y2015x7y3z4问题:三家连锁店以相同的价格m(单位:元/瓶)销售某种商品,它们在一个月内的销售量(单位:瓶)分别是a,b,c你能用不同的方法计算它们在这个月内销售这种商品的总收入吗?由于①②均表示总收入,所以:m﹙a+b+c﹚=ma+mb+mc单项式与多项式相乘,就是用单项式去乘多项式的每一项,把所得的积相加。 m﹙a+b+c﹚mambmc﹙a+b+c﹚解:(1) (-4x2). (3x+1)
= (-4x2). (3x)+ (-4x2)·1
=(-4×3).(x2. x)+(-4x2)
=-12x3 -4x2 (2)
练习:1、计算
(1)3a(5a-2b) (2)(x-3y)(-6x)
2、化简:x(x-1)+2x(x+1)-3x(2x-5)答案:1、(1)15a2-6ab (2)-6x2+18yx
2、-3x2+16xb窗口矮柜右侧矮柜mn图5-5a我们怎样来表示此厨房的总面积呢 ?a+bm+nabambmmab窗口矮柜右侧矮柜mn图5-5图5-6图5-7由图5-6,可得总面积为 (a+b)(m+n);由图5-7,可得总面积为 a(m+n)+b(m+n) 或 am+an+bm+nn.anbnna(1) (2) (3) anbm a+babanbmam + an + bm + bn=+++(a+b)(m+n)=am1234+an+bm+bn多项式的乘法法则:(1) (x+2y)(5a+3b) ;(2) (2x–3)(x+4) ;解:(x+2y)(5a+3b) ==解:(2x–3)(x+4)2x2 +8x –3x –12=2x2 +5x例1 计算:=–12x ·5a +x ·3b +2y ·5a +2y ·3b5ax+3bx+10ay+6by 练习一、计算:(1) (2n+6)(n–3);(2) (2x+3)(3x–1);例2,先化简,再求值:
(2a-3)(3a+1)-6a(a-4),其中a=解:原式=17a-3,则当a=
17a-3=1练习二、计算: 1、漏乘 需要注意的几个问题2、符号问题 3、最后结果应化成最简形式。判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由。解:原式判别下列解法是否正确,若错请说出理由。解:原式延伸训练:填空:观察上面四个等式,你能发现什么规律?你能根据这个规律解决下面的问题吗?5 61 (-6)(-1) (-6)(-5) 6口答:学了这节课,你有什么收获? 说一说:小结:
1.运用多项式的乘法法则时,必须做到不重不漏.
2.多项式与多项式相乘,仍得多项式.
3.注意确定积中的每一项的符号,多项式中每一项都包含它前面的符号,“同号得正,异号得负”.
4.多项式与多项式想乘的展开式中,有同类项要合并同类项. 能力拓展若(x3+mx+n)(x2-5x+3)展开后不含x3和x2项,试求m,n的值.
