生活中的优化问题举例

课件26张PPT。人教A版高中数学选修1-1
多媒体课件 3.4
生活中的优化问题举例第三章 导数及其应用生活中经常遇到求利润最大、用料最省、
效率最高等问题，这些问题通常被称为
优化问题。例1、汽油的使用效率何时最高汽油的消耗量w（单位：L）与汽车的速度
v（单位：km/h）之间有一定的关系，汽油
的消耗量w是汽车速度v的函数。
根据你的生活经验，思考下面两个问题：(1)是不是汽车的速度越快，汽油的消耗量
越大？(2)“汽油的使用效率最高”的含义是什么？分析：
汽油的使用效率（单位：L/km）
=汽油消耗量÷汽车行驶路程如果用G表示每千米平均的汽油消耗量，
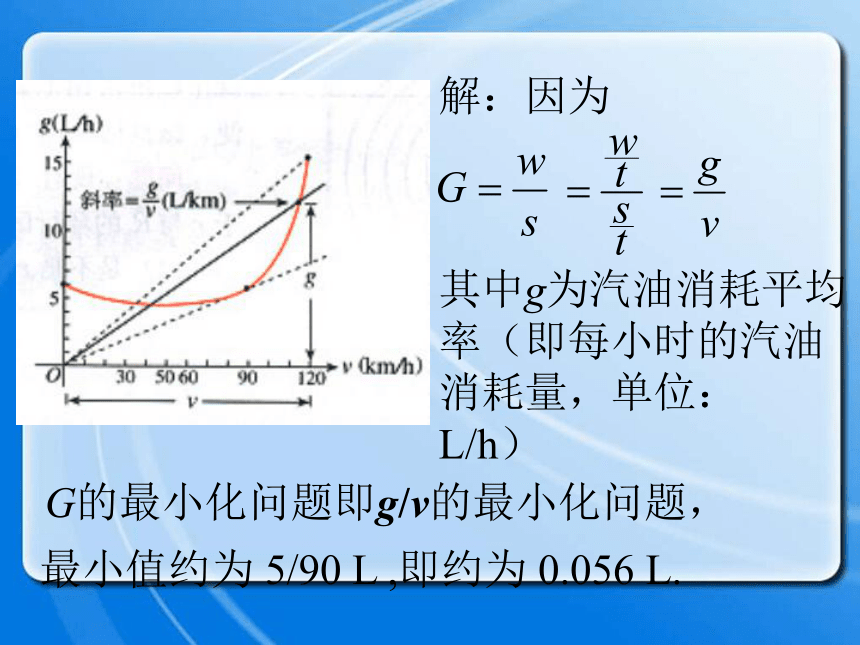
s表示汽车行驶的路程(单位：km),则解：因为其中g为汽油消耗平均率（即每小时的汽油消耗量，单位：
L/h）G的最小化问题即g/v的最小化问题，最小值约为 5/90 L ,即约为 0.056 L.例2、磁盘的最大存储量问题(1) 你知道计算机是如何存储、检索信息的吗？
(2) 你知道磁盘的结构吗？(3)如何使一个圆环状的磁
盘存储尽可能多的信息？问题：现有一张半径为R的磁盘，它的存储区是半径介于r与R的环行区域。是不是r越小，磁盘的存
储量越大？(2) r为多少时，磁盘具有最大存储量
（最外面的磁道不存储任何信息）？解：存储量=磁道数×每磁道的比特数(1) 它是一个关于r的二次函数，从函数的解析式可以判断，不是r越小，磁盘的存储量越大。(2) 为求f(r)的最大值，先计算解得例3、饮料瓶大小对饮料公司利润的影响你是否注意过，市场上等量的小包装
的物品一般比大包装的要贵些？你想从数
学上知道它的道理吗？(2) 是不是饮料瓶越大，饮料公司的利润
越大？某制造商制造并出售球形瓶装的某种饮料，瓶子的制造成本是0.8?r2分，其中r 是瓶子的半径，单位是厘米，已知每出售1 ml的饮料，制造商可获利0.2分，且制造商能制作的瓶子的最大半径为6 cm.问题：(1)瓶子半径多大时，能使每瓶饮料的利润最大？
(2)瓶子半径多大时，每瓶饮料的利润最 小？解:由于瓶子的半径为r,
所以每瓶饮料的利润是1、当半径为2cm时,利润最小,这时f(2)<0,2、当半径为6cm时，利润最大。从图中可以看出:从图中，你还能看出什么吗？解决优化问题的基本思路：优化问题用导数解决
数学问题优化问题
的答案用函数表示的
数学问题练习1、一条长为l的铁丝截成两段，分别
弯成两个正方形，要使两个正方形
的面积和最小，两段铁丝的长度分
别是多少？则两个正方形面积和为由问题的实际意义可知：练习2、 如图,在二次函数f(x)=4x-x2的图象与x轴所围成的图形中有一个内接矩形ABCD,求这个矩形的最大面积.解:设B(x,0)(0 则 A(x, 4x-x2).从而|AB|= 4x-x2,
|BC|=2(2-x).
故矩形ABCD的面积为:
S(x)=|AB||BC|=2x3-12x2+16x(0矩形的最大面积是令 ,得所以当 时,练习3、用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.解:设容器底面短边长为xm,则另一边长为
(x+0.5)m,容器的高为
[14.8-4x-4(x+0.5)]/4=3.2-2x.由问题的实际意义,要求x>0,3.2-2x>0,
解得x的取值范围是0则y=x(x+0.5)(3.2-2x) (0即有y=-2x3+2.2x2+1.6x (0得y最大=-2+2.2+1.6=1.8,
这时容器的高为3.2-2x=1.2. 小结解决优化问题的基本思路：优化问题用导数解决
数学问题优化问题
的答案用函数表示的
数学问题再见