空间向量的数乘运算
图片预览




文档简介
课件23张PPT。第三章 空间向量与立体几何3.1空间向量及其运算
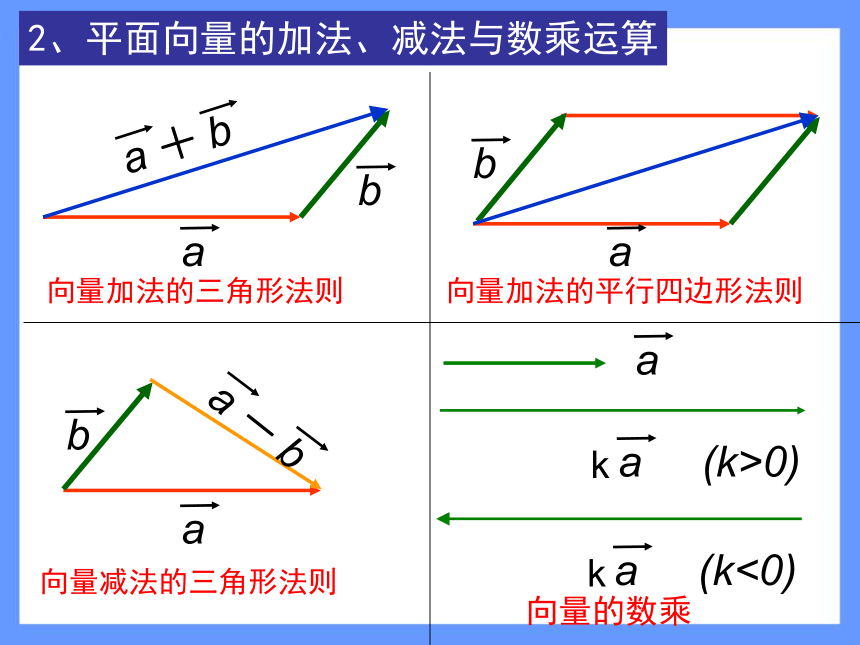
3.1.2空间向量的数乘运算2、平面向量的加法、减法与数乘运算向量加法的三角形法则加法
减法
数乘
运算数乘:ka,k为正数,负数,零数乘分配律平面向量概念运
算
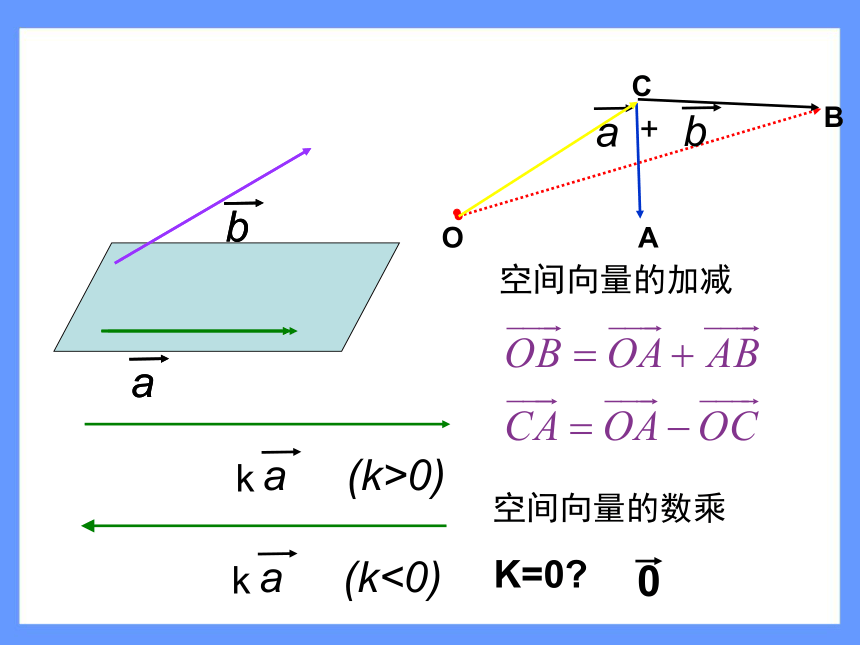
律减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律具有大小和方向的量空间向量及其加减运算空间向量的数乘K=0?0OABC空间向量的加减数乘分配律数乘:ka,k为正数,负数,零加法
减法
数乘
运算数乘:ka,k为正数,负数,零数乘分配律平面向量概念运
算
律减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律具有大小和方向的量空间向量及其加减运算加法交换律加法:三角形法则或
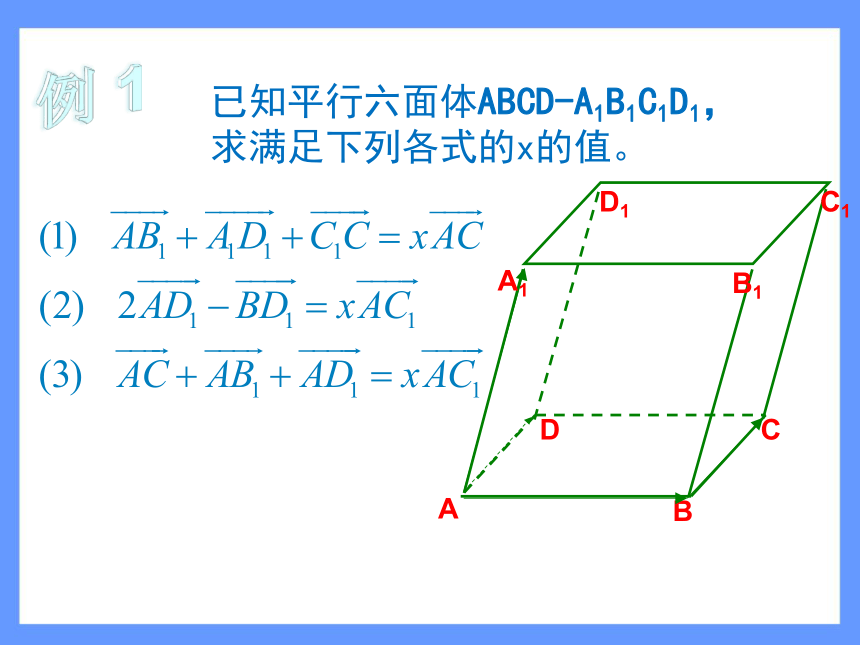
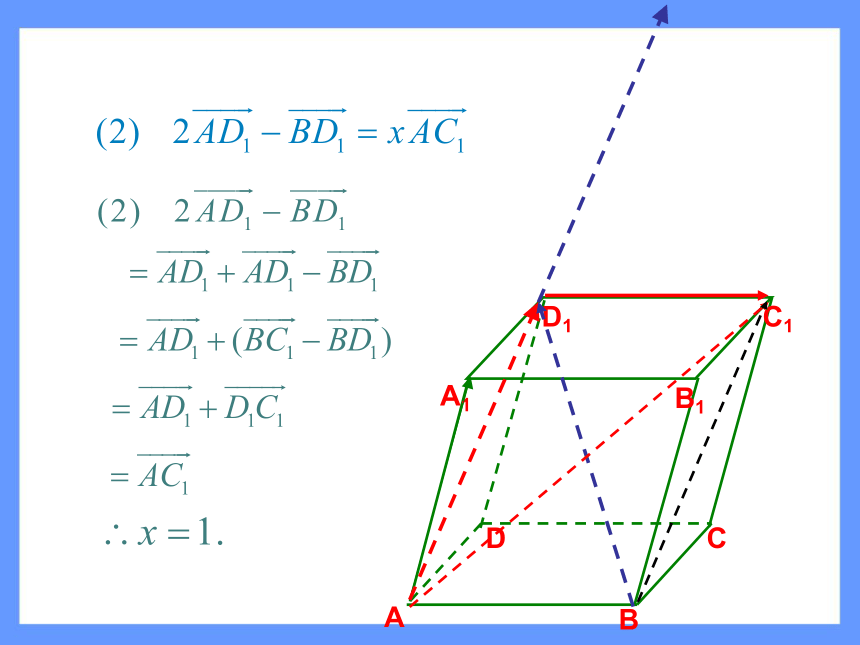
平行四边形法则减法:三角形法则加法结合律已知平行六面体ABCD-A1B1C1D1,
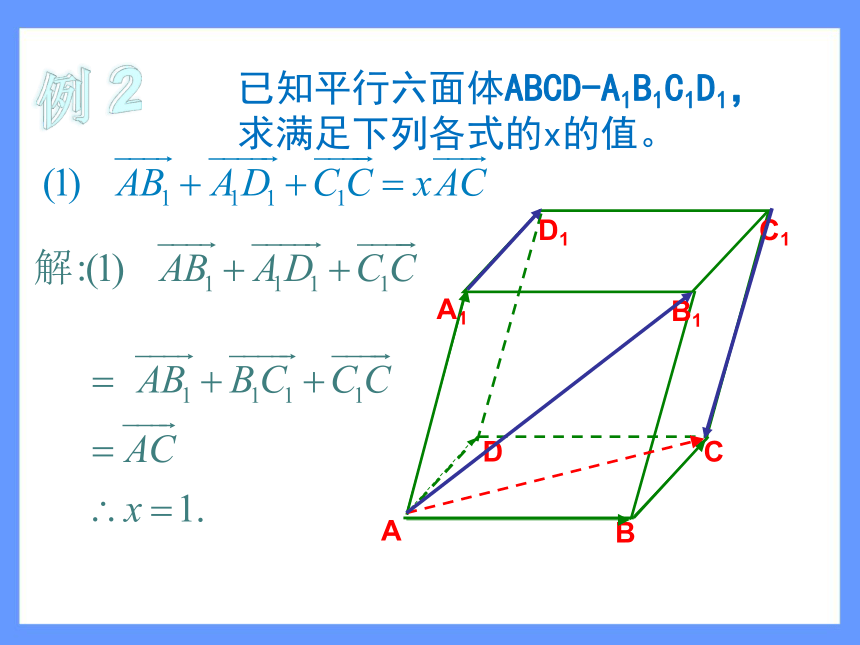
求满足下列各式的x的值。例 1已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例 2一、共线向量:零向量与任意向量共线.共线向量与共面向量 若P为A,B中点, 则1.下列说明正确的是:
A.在平面内共线的向量在空间不一定共线
B.在空间共线的向量在平面内不一定共线
C.在平面内共线的向量在空间一定不共线
D.在空间共线的向量在平面内一定共线2.下列说法正确的是:
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面
C.空间的任意两个向量都共面
D.空间的任意三个向量都共面练习 一DC例1 已知A、B、P三点共线,O为空间任
意一点,且 ,求 的值. 二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。2.共面向量定理:如果两个向量
不共线,则向量 与向量 共面的充要
条件是存在实数对 使 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使
或对空间任一点O,有
练习 二D例3 对空间任意一点O和不共线的三点
A、B、C,试问满足向量关系式
(其中 )的四点P、A、B、
C是否共面?例4 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?例1.已知三点 不共线,对平面外任一点P,满足条件, 试判断:点P与是否一定共面?空间向量的数乘运算小结123共线向量的概念与共线向量定理共面向量的概念与共面向量定理谢谢
3.1.2空间向量的数乘运算2、平面向量的加法、减法与数乘运算向量加法的三角形法则加法
减法
数乘
运算数乘:ka,k为正数,负数,零数乘分配律平面向量概念运
算
律减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律具有大小和方向的量空间向量及其加减运算空间向量的数乘K=0?0OABC空间向量的加减数乘分配律数乘:ka,k为正数,负数,零加法
减法
数乘
运算数乘:ka,k为正数,负数,零数乘分配律平面向量概念运
算
律减法:三角形法则加法:三角形法则或平行四边形法则空间向量具有大小和方向的量加法交换律加法结合律具有大小和方向的量空间向量及其加减运算加法交换律加法:三角形法则或
平行四边形法则减法:三角形法则加法结合律已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例 1已知平行六面体ABCD-A1B1C1D1,
求满足下列各式的x的值。例 2一、共线向量:零向量与任意向量共线.共线向量与共面向量 若P为A,B中点, 则1.下列说明正确的是:
A.在平面内共线的向量在空间不一定共线
B.在空间共线的向量在平面内不一定共线
C.在平面内共线的向量在空间一定不共线
D.在空间共线的向量在平面内一定共线2.下列说法正确的是:
A.平面内的任意两个向量都共线
B.空间的任意三个向量都不共面
C.空间的任意两个向量都共面
D.空间的任意三个向量都共面练习 一DC例1 已知A、B、P三点共线,O为空间任
意一点,且 ,求 的值. 二.共面向量:1.共面向量:平行于同一平面的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。2.共面向量定理:如果两个向量
不共线,则向量 与向量 共面的充要
条件是存在实数对 使 推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使
或对空间任一点O,有
练习 二D例3 对空间任意一点O和不共线的三点
A、B、C,试问满足向量关系式
(其中 )的四点P、A、B、
C是否共面?例4 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?例1.已知三点 不共线,对平面外任一点P,满足条件, 试判断:点P与是否一定共面?空间向量的数乘运算小结123共线向量的概念与共线向量定理共面向量的概念与共面向量定理谢谢
