空间向量的数量积运算
图片预览






文档简介
课件18张PPT。第三章 空间向量与立体几何3.1空间向量及其运算
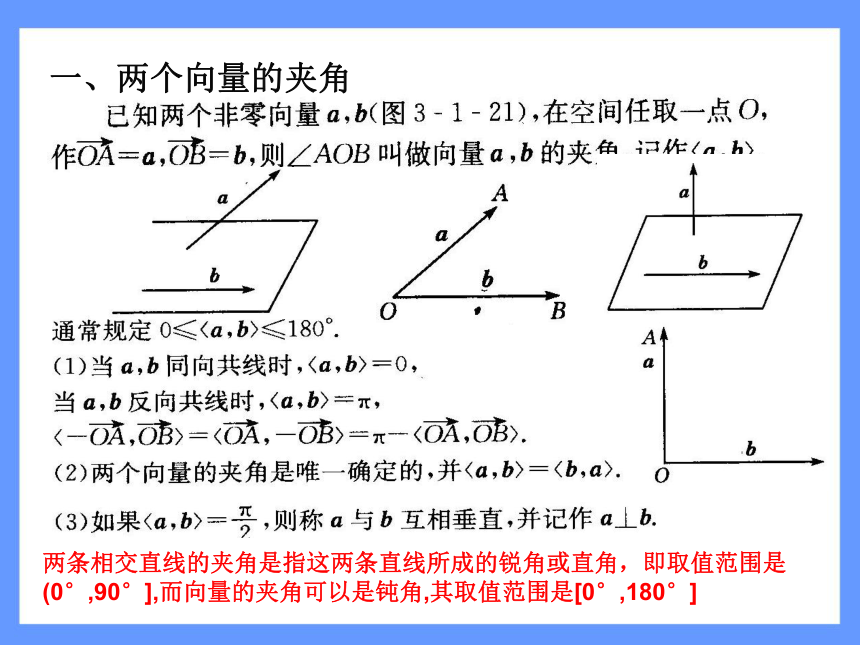
3.1.3空间向量的数量积运算一、两个向量的夹角两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]练习 1二、两个向量的数量积注意:
(1)两个向量的数量积,其结果是个数量,而不是向量,它的值为两向量的模与两向量夹角的余弦的乘积,其符号由夹角的余弦值决定.
(2)两个向量的数量积是两个向量之间的一种乘法,与以前学过的数的乘法是有区别的,因此我们书写向量的数量积时,只能用符号a·b,而不能用a×b,也不能用ab.练习 2三、空间两个向量的数量积的性质(1)空间向量的数量积具有和平面向量的数量积完全相同的性质
(2)性质(2)是用来判断两个向量是否垂直,性质(5)是用来求
两个向量的夹角.
(3)性质(3)是实数与向量之间转化的依据.已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.证明:例 1四、空间向量数量积的运算律与平面向量一样,空间向量的数量积满足如下运算律: 向量数量积的运算适合乘法结合律吗?
即(a?b)c一定等于a(b·c)吗?已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,计算:(1)(a+2b)·(2n-b);(2)|4a一2b|.例 2Aa在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。已知:如图,PO,PA分别是平面α的垂线,斜线,AO是PA在平面α内的射影,例 3如图,m,n是平面α内的两条相交直线。如果l⊥m,l⊥n,求证:l⊥α例 4五、三垂线定理及其逆定理 (1)相关概念
①正射影:已知平面a和一点A,过点A作a的垂线l与a
相交于点A’,则A’就是点A在平面a内的正射影,简称射影. ②斜线:如果一条直线AB和平面a相交点B,但不和a垂直,那么直线AB叫做这个平面的斜线,斜线和平面的交点B叫做斜足,斜线上一点A与斜足B之间的线段叫做斜线段AB.(2)三垂线定理:在平面内的一 条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
(3)三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.(1)三垂线定理及其逆定理中都出现了四条线AB,AC,BC,l,定理中所描述的是AC(斜线)、BC(射影)、l(面内的直线)之间的关系.
在三垂线定理及其逆定理中,涉及上面四条线,三个垂直
关系①垂线AB和平面a垂直;
②射影BC和直线l垂直;
③斜线AC和直线l垂直,
所以定理称为“三垂线定理”.(2)两个定理的区别
①从两个定理的条件和结论上区分,三垂线定理是“线与射影垂直推出 线与斜线垂直”,逆定理相反.
②从两个定理的作用上区分,三垂线定理解决已知“共面直线垂直推出 异面直线垂直”,逆定理相反. (3)利用三垂线定理及其逆定理的关键是要善于从各种图
形中找出“平面的垂线”“平面的斜线”“斜线的射影”.
(4)三垂线正逆定理是立体几何中重要定理,是共面两直线的垂直关系与空间两直线的垂直关系之间相互转化的判定定理,
它的实质是通过线线垂直得到线面垂直又转化为线线垂直,它是证线线垂直的重要方法,
它的用途是在作图中,作二面角的平面角;在证题中,证线线垂直;在计算中,用归面法归拢已知条件便于计算.在四面体ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.练习 3两个向量的夹角小结123两个向量的数量积空间向量数量积的运算律4三垂线定理谢谢
3.1.3空间向量的数量积运算一、两个向量的夹角两条相交直线的夹角是指这两条直线所成的锐角或直角,即取值范围是(0°,90°],而向量的夹角可以是钝角,其取值范围是[0°,180°]练习 1二、两个向量的数量积注意:
(1)两个向量的数量积,其结果是个数量,而不是向量,它的值为两向量的模与两向量夹角的余弦的乘积,其符号由夹角的余弦值决定.
(2)两个向量的数量积是两个向量之间的一种乘法,与以前学过的数的乘法是有区别的,因此我们书写向量的数量积时,只能用符号a·b,而不能用a×b,也不能用ab.练习 2三、空间两个向量的数量积的性质(1)空间向量的数量积具有和平面向量的数量积完全相同的性质
(2)性质(2)是用来判断两个向量是否垂直,性质(5)是用来求
两个向量的夹角.
(3)性质(3)是实数与向量之间转化的依据.已知空间四边形OABC中,M,N,P,Q分别为BC,AC,OA,OB的中点,若AB=OC,求证:PM⊥QN.证明:例 1四、空间向量数量积的运算律与平面向量一样,空间向量的数量积满足如下运算律: 向量数量积的运算适合乘法结合律吗?
即(a?b)c一定等于a(b·c)吗?已知空间向量a,b满足|a|=4,|b|=8,a与b的夹角是150°,计算:(1)(a+2b)·(2n-b);(2)|4a一2b|.例 2Aa在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。已知:如图,PO,PA分别是平面α的垂线,斜线,AO是PA在平面α内的射影,例 3如图,m,n是平面α内的两条相交直线。如果l⊥m,l⊥n,求证:l⊥α例 4五、三垂线定理及其逆定理 (1)相关概念
①正射影:已知平面a和一点A,过点A作a的垂线l与a
相交于点A’,则A’就是点A在平面a内的正射影,简称射影. ②斜线:如果一条直线AB和平面a相交点B,但不和a垂直,那么直线AB叫做这个平面的斜线,斜线和平面的交点B叫做斜足,斜线上一点A与斜足B之间的线段叫做斜线段AB.(2)三垂线定理:在平面内的一 条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直.
(3)三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在平面内的射影垂直.(1)三垂线定理及其逆定理中都出现了四条线AB,AC,BC,l,定理中所描述的是AC(斜线)、BC(射影)、l(面内的直线)之间的关系.
在三垂线定理及其逆定理中,涉及上面四条线,三个垂直
关系①垂线AB和平面a垂直;
②射影BC和直线l垂直;
③斜线AC和直线l垂直,
所以定理称为“三垂线定理”.(2)两个定理的区别
①从两个定理的条件和结论上区分,三垂线定理是“线与射影垂直推出 线与斜线垂直”,逆定理相反.
②从两个定理的作用上区分,三垂线定理解决已知“共面直线垂直推出 异面直线垂直”,逆定理相反. (3)利用三垂线定理及其逆定理的关键是要善于从各种图
形中找出“平面的垂线”“平面的斜线”“斜线的射影”.
(4)三垂线正逆定理是立体几何中重要定理,是共面两直线的垂直关系与空间两直线的垂直关系之间相互转化的判定定理,
它的实质是通过线线垂直得到线面垂直又转化为线线垂直,它是证线线垂直的重要方法,
它的用途是在作图中,作二面角的平面角;在证题中,证线线垂直;在计算中,用归面法归拢已知条件便于计算.在四面体ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.练习 3两个向量的夹角小结123两个向量的数量积空间向量数量积的运算律4三垂线定理谢谢
