函数的单调性说课件
图片预览





文档简介
课件25张PPT。石脑中学 吴超火 北师大版普通高中课程标准实验教科书数学(必修1) 《函数的单调性》
(说课)一.说教材本课是北师大版数学(必修1)第二章第3节的内容。函数的单调性是函数的重要性质,利用函数的单调性可以比较两个数的大小,求函数的值域等等。所以这是一节非常重要的内容,在教材中起到承上启下的作用。理解函数单调性意义;会判断和证明简单函数的单调性。 培养学生观察问题、分析问题和解决问题的能力,培养学生数形结合的思想。一.说教材培养学生细心观察、认真分析、严谨论证的良好思维习惯。 函数单调性的概念 根据定义证明函数的单调性一.说教材由于判断和证明函数的单调性时,常常要综合运用一些知识(如不等式、因式分解以及数形结合的思想方法等),因此函数单调性的判断或证明是本节的一个难点。多媒体投影
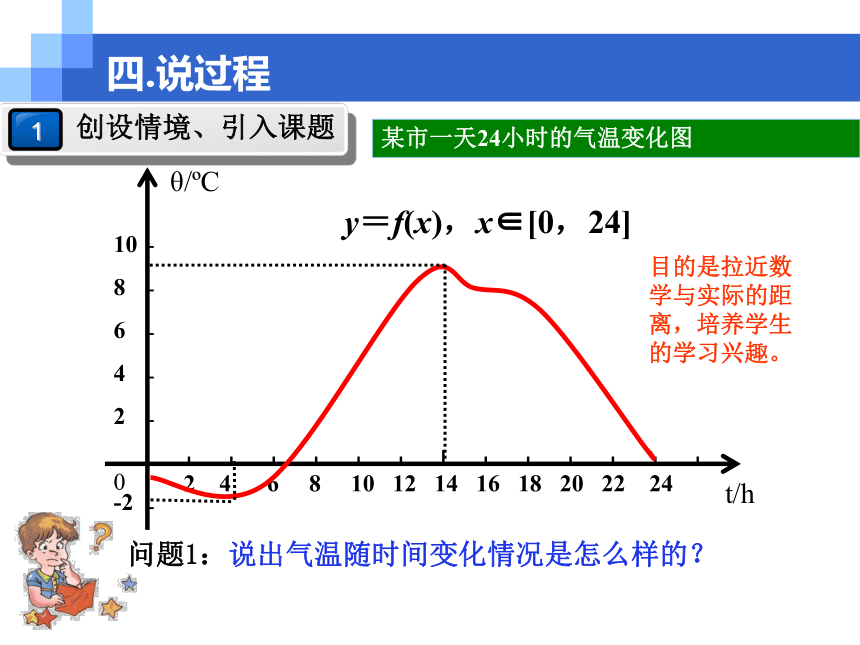
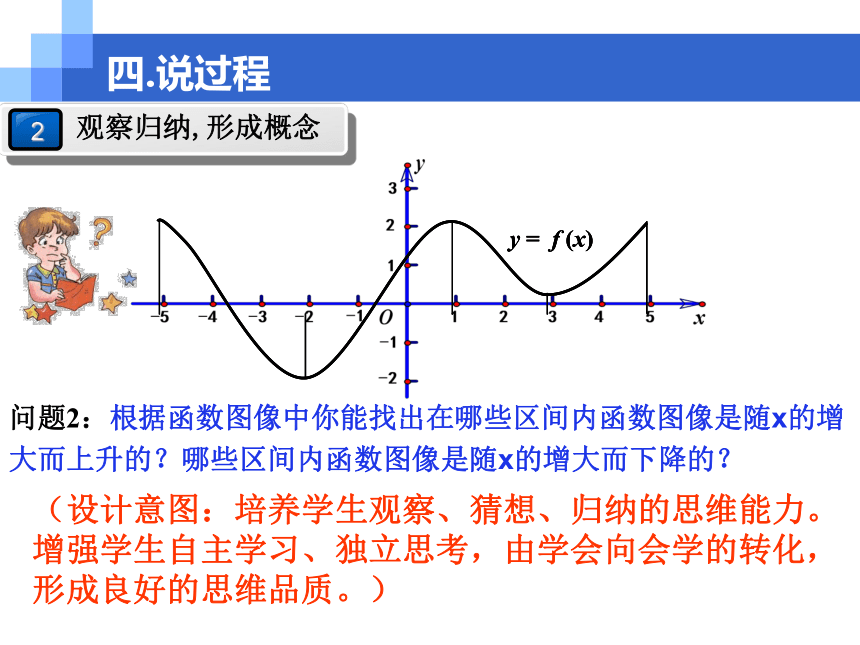
二.说教法启发引导式教学方法 三.说学法 其次,利用直观图形启迪学生思维,并通过例题和练习,来完成从感性认 识到理性认识的飞跃。 首先,普通班学生基础一般较差,采用多媒体教学,能够激发学生的学习兴趣。 另外,让学生从问题中质疑、尝试、归纳、总结。培养学生发现问题、研 究问题和解决问题的能力。四.说过程y=f(x),x∈[0,24]问题1:说出气温随时间变化情况是怎么样的?四.说过程某市一天24小时的气温变化图 目的是拉近数学与实际的距离,培养学生的学习兴趣。 问题2:根据函数图像中你能找出在哪些区间内函数图像是随x的增大而上升的?哪些区间内函数图像是随x的增大而下降的?四.说过程(设计意图:培养学生观察、猜想、归纳的思维能力。增强学生自主学习、独立思考,由学会向会学的转化,形成良好的思维品质。)
问题3:根据观察结果如何使用数学语言进行归纳?四.说过程(设计意图:这是一个难点,应让学生充分讨论,拿出自己的思路。在此过程中教师可以引导有关“增大”,“减小”等概念是怎样用数学符号体现出来的,比较是体现增大或减小的一种方式.)
四.说过程函数的单调性定义最后由教师板书定义,给出函数单调性的概念。(让学生自己先进行思考交流)一般地,函数f(x)的定义域为I:四.说过程问题4:在定义中我们应该抓住哪些关键词语?(设计意图:使学生更透彻的理解单调性定义)理解概念应抓住关键词:“给定区间”,“属于”,“任意”,“都有”这几个关键词语。这一区间叫函数的单调区间问题5:单调区间图像特征是怎么样的呢?在单调增区间上函数的图像是上升的。在单调减区间上函数的图像是下降的。四.说过程(设计意图:使学生更准确地把握概念,理解函数的单调性是对某个区间而言的,它是一个局部概念。函数的单调性其实也叫做函数的增减性)
mn
y=f(x)yyY=2x+1增区间为增区间为减区间为例1:写出函数的单调区间四.说过程增区间为写出函数的单调区间四.说过程(设计意图:使学生了解,从图象上观察是判断函数在某一区间上是否具有单调性的一种常用而又直观的方法,通过本例可以培养学生数形结合的思想)
【即时训练】
1、判断函数f(x)=1/x在(-∞,0)上是递增的还是递减的?
递减的2、判断函数f(x)=1/x在(0,+∞)上是递增的还是递减的?
递减的【想一想】能否说函数y=f(x)=1/x在(-∞,+∞)上是递减的?
答:不能. 因为x=0不属于f(x)=1/x的定义域.四.说过程(设计意图) 通过学生观察、讨论,教师的引导来巩固 新知。同时提醒学生在写单调区间时不要轻易用并集的符号连接,而应用“和”连接。1. 取值:2.作差、变形:
3.定号、下结论:问题6:怎么判断函数单调性?(师生共同探讨) f(x 1)-f(x 2)变形要化到最简单形式 在给定区间上任取两个实数x1 , x2 , 且x1 < x2 。结论一定要指出在哪个区间上。四.说过程(设计意图:通过问题6与学生共同探讨得出判断函数单调性的解题基本步骤,从而突破本节难点,并为接下来的例2作铺垫)例2: 证明:函数 f ( x ) = 3x+2 在 R上是单调增函数。证明:设 x 1 ,x 2是R上的任意两个值,且x 1 < x 2,则 f ( x 1 ) -f ( x 2 )= 3 (x 1 -x 2 )∵x 1 < x 2 ,∴x 1 - x 2< 0∴f ( x 1 ) -f ( x 2 ) < 0即f ( x 1 ) < f ( x 2 )所以,函数 f ( x ) = 3x+2 在 R上是单调增函数。四.说过程(设计意图:通过例2可引导学生进一步概括出证明函数单调性方法及步骤,从而突破本节的难点,同时提示学生注意证明过程的规范性及严谨性。)→作差→取值→变形→定号→下结论课堂练习: 课本P39:4
(设计意图):通过课堂练习使学生进一步掌握证明函数单调性的方法和步骤,从而达到消化、巩固新知的目的。)
四.说过程4.作函数f ( x ) = -3x+4的图像, 并证明它是 R上是增函数。这节课我们的收获是什么?四.说过程
这节课我们学习了函数单调性的定义,
要特别注意定义中“给定区间”,“属于”,“任意”“都有”这几个关键词语;在写单调区间时不要轻易用并集的符号连接;最后在用定义证明函数的单调性时,应该注意证明的几个步骤。四.说过程这里我让学生集体回顾,归纳,同时教师补充整理。小结:通过小结,使学生对本节课所学知识的结构有 一个明晰的认识,使能抓住重点进行课后复习。四.说过程反思:上完这节课后,我发现利用多媒体教学能够激发学生的学习兴趣;另外基于普通班的学生基础较差,使学生达到教学目标有点难度。课本第39页练习第5题板书设计、作业课后作业:课后思考:B组第2题(设计意图:考虑到学生的差异性我对课后作业我实行分层设置,包括书面作业、课后思考题两部分. 这样既使学生掌握基础知识,又使学有余力的学生有所提高。)函数的单调性
函数单调性定义 例题讲解
例1: 课堂作业
证明函数单调性的步骤 例2: 布置作业
注意 小结
1、
2、
3、板书设计欢迎各位领导老师批评、指正
谢谢!
(说课)一.说教材本课是北师大版数学(必修1)第二章第3节的内容。函数的单调性是函数的重要性质,利用函数的单调性可以比较两个数的大小,求函数的值域等等。所以这是一节非常重要的内容,在教材中起到承上启下的作用。理解函数单调性意义;会判断和证明简单函数的单调性。 培养学生观察问题、分析问题和解决问题的能力,培养学生数形结合的思想。一.说教材培养学生细心观察、认真分析、严谨论证的良好思维习惯。 函数单调性的概念 根据定义证明函数的单调性一.说教材由于判断和证明函数的单调性时,常常要综合运用一些知识(如不等式、因式分解以及数形结合的思想方法等),因此函数单调性的判断或证明是本节的一个难点。多媒体投影
二.说教法启发引导式教学方法 三.说学法 其次,利用直观图形启迪学生思维,并通过例题和练习,来完成从感性认 识到理性认识的飞跃。 首先,普通班学生基础一般较差,采用多媒体教学,能够激发学生的学习兴趣。 另外,让学生从问题中质疑、尝试、归纳、总结。培养学生发现问题、研 究问题和解决问题的能力。四.说过程y=f(x),x∈[0,24]问题1:说出气温随时间变化情况是怎么样的?四.说过程某市一天24小时的气温变化图 目的是拉近数学与实际的距离,培养学生的学习兴趣。 问题2:根据函数图像中你能找出在哪些区间内函数图像是随x的增大而上升的?哪些区间内函数图像是随x的增大而下降的?四.说过程(设计意图:培养学生观察、猜想、归纳的思维能力。增强学生自主学习、独立思考,由学会向会学的转化,形成良好的思维品质。)
问题3:根据观察结果如何使用数学语言进行归纳?四.说过程(设计意图:这是一个难点,应让学生充分讨论,拿出自己的思路。在此过程中教师可以引导有关“增大”,“减小”等概念是怎样用数学符号体现出来的,比较是体现增大或减小的一种方式.)
四.说过程函数的单调性定义最后由教师板书定义,给出函数单调性的概念。(让学生自己先进行思考交流)一般地,函数f(x)的定义域为I:四.说过程问题4:在定义中我们应该抓住哪些关键词语?(设计意图:使学生更透彻的理解单调性定义)理解概念应抓住关键词:“给定区间”,“属于”,“任意”,“都有”这几个关键词语。这一区间叫函数的单调区间问题5:单调区间图像特征是怎么样的呢?在单调增区间上函数的图像是上升的。在单调减区间上函数的图像是下降的。四.说过程(设计意图:使学生更准确地把握概念,理解函数的单调性是对某个区间而言的,它是一个局部概念。函数的单调性其实也叫做函数的增减性)
mn
y=f(x)yyY=2x+1增区间为增区间为减区间为例1:写出函数的单调区间四.说过程增区间为写出函数的单调区间四.说过程(设计意图:使学生了解,从图象上观察是判断函数在某一区间上是否具有单调性的一种常用而又直观的方法,通过本例可以培养学生数形结合的思想)
【即时训练】
1、判断函数f(x)=1/x在(-∞,0)上是递增的还是递减的?
递减的2、判断函数f(x)=1/x在(0,+∞)上是递增的还是递减的?
递减的【想一想】能否说函数y=f(x)=1/x在(-∞,+∞)上是递减的?
答:不能. 因为x=0不属于f(x)=1/x的定义域.四.说过程(设计意图) 通过学生观察、讨论,教师的引导来巩固 新知。同时提醒学生在写单调区间时不要轻易用并集的符号连接,而应用“和”连接。1. 取值:2.作差、变形:
3.定号、下结论:问题6:怎么判断函数单调性?(师生共同探讨) f(x 1)-f(x 2)变形要化到最简单形式 在给定区间上任取两个实数x1 , x2 , 且x1 < x2 。结论一定要指出在哪个区间上。四.说过程(设计意图:通过问题6与学生共同探讨得出判断函数单调性的解题基本步骤,从而突破本节难点,并为接下来的例2作铺垫)例2: 证明:函数 f ( x ) = 3x+2 在 R上是单调增函数。证明:设 x 1 ,x 2是R上的任意两个值,且x 1 < x 2,则 f ( x 1 ) -f ( x 2 )= 3 (x 1 -x 2 )∵x 1 < x 2 ,∴x 1 - x 2< 0∴f ( x 1 ) -f ( x 2 ) < 0即f ( x 1 ) < f ( x 2 )所以,函数 f ( x ) = 3x+2 在 R上是单调增函数。四.说过程(设计意图:通过例2可引导学生进一步概括出证明函数单调性方法及步骤,从而突破本节的难点,同时提示学生注意证明过程的规范性及严谨性。)→作差→取值→变形→定号→下结论课堂练习: 课本P39:4
(设计意图):通过课堂练习使学生进一步掌握证明函数单调性的方法和步骤,从而达到消化、巩固新知的目的。)
四.说过程4.作函数f ( x ) = -3x+4的图像, 并证明它是 R上是增函数。这节课我们的收获是什么?四.说过程
这节课我们学习了函数单调性的定义,
要特别注意定义中“给定区间”,“属于”,“任意”“都有”这几个关键词语;在写单调区间时不要轻易用并集的符号连接;最后在用定义证明函数的单调性时,应该注意证明的几个步骤。四.说过程这里我让学生集体回顾,归纳,同时教师补充整理。小结:通过小结,使学生对本节课所学知识的结构有 一个明晰的认识,使能抓住重点进行课后复习。四.说过程反思:上完这节课后,我发现利用多媒体教学能够激发学生的学习兴趣;另外基于普通班的学生基础较差,使学生达到教学目标有点难度。课本第39页练习第5题板书设计、作业课后作业:课后思考:B组第2题(设计意图:考虑到学生的差异性我对课后作业我实行分层设置,包括书面作业、课后思考题两部分. 这样既使学生掌握基础知识,又使学有余力的学生有所提高。)函数的单调性
函数单调性定义 例题讲解
例1: 课堂作业
证明函数单调性的步骤 例2: 布置作业
注意 小结
1、
2、
3、板书设计欢迎各位领导老师批评、指正
谢谢!
