不等式的性质(一)

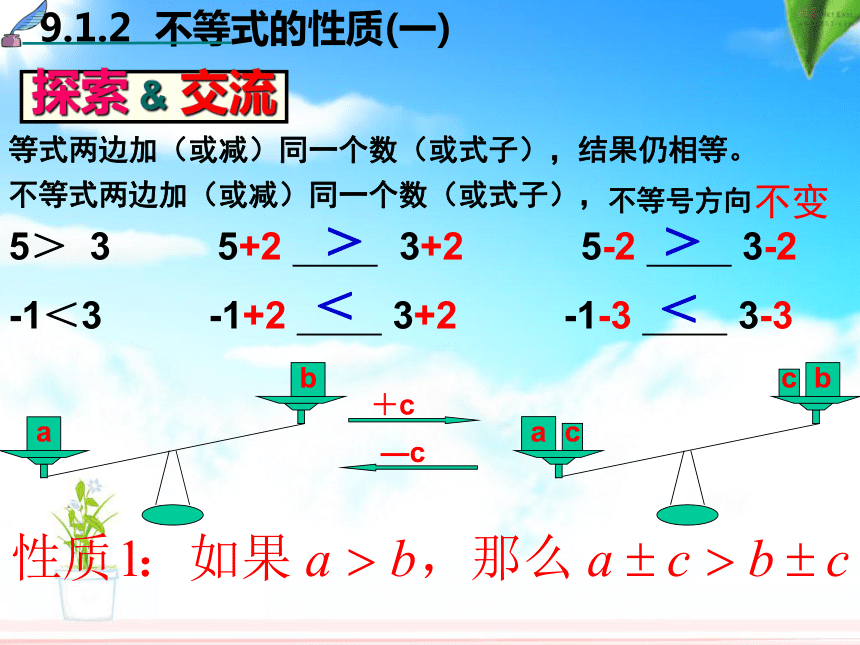
课件17张PPT。不等式的性质（一）问题：刘翔想在12.8秒以内跑到110米栏的终点,那么他平均每秒钟至少要跑多少米呢?解：设平均每秒钟至少要跑x米，则由题意得：12.8x＞110?同学们还记得等式的性质吗?(1)等式两边加 (或减)同一个数（或式子）, 结果仍相等. (2)等式两边都乘以同一个数，或除以同一个不为0的数, 结果仍相等.若 a=b,则 a+c = b+c(或a-c=b-c)等式两边加（或减）同一个数（或式子），结果仍相等。不等式两边加（或减）同一个数（或式子），不等号方向不变5＞ 3 5+2 3+2 5-2 3-2
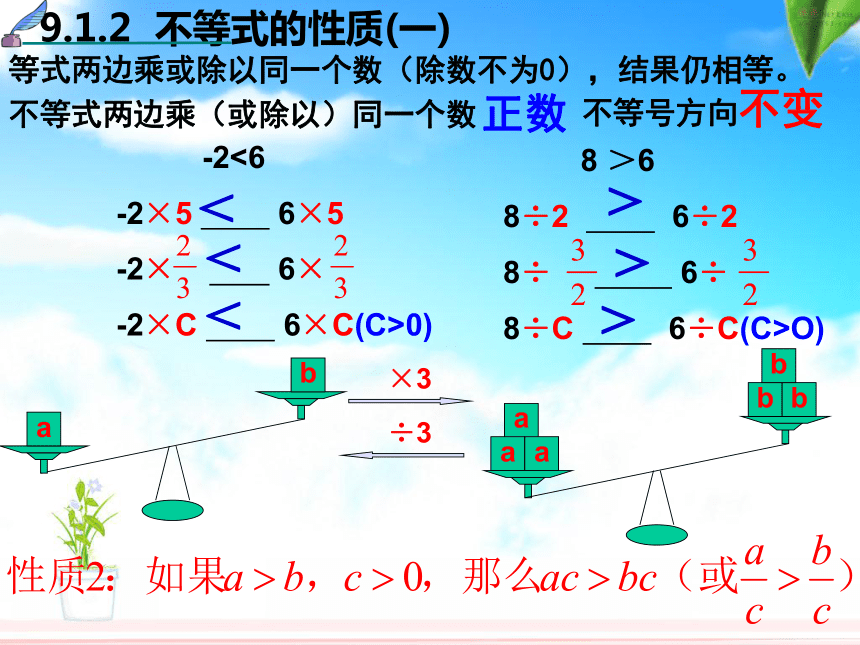
-1＜3 -1+2 3+2 -1-3 3-3＞＞＜＜探索 & 交流等式两边乘或除以同一个数（除数不为0），结果仍相等。＞＞＞＜＜＜不等式两边乘（或除以）同一个数正数不等号方向不变 8 ＞6
8÷2 6÷2
8÷ 6÷
8÷C 6÷C(C>O) -2<6
-2×5 6×5
-2× 6×
-2×C 6×C(C>0)＞＞＞＜＜＜不等式两边乘（或除以）同一个负数不等号方向改变 2<6
2×(-5) 6×(-5)
2× 6×
2×C 6×C(C<0) 8 ＞-6
8÷(-2) -6÷(-2 )
8÷ -6÷
8÷C -6÷C(C 括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
∴ a 2b( ) ∴ a 9( ) ＞＞＞＜＜＜不等式
性质1不等式
性质3不等式
性质3不等式
性质2不等式
性质1不等式
性质3判断对错并说明理由1. 若a < b,则3a < 3b ( )2. 若-6a<-6b,则a < b ( )3. 若a > 0,则3a > 2a ( )√√×? 说一说 ? 4. 若ab < 0,则a<0,b>0 ( )5. 若a-b > a,则b < 0 ( )6. 若ab+c ( )7. 若ac b,则ac2 > bc2 ( )9. 若a>b, c>d ,则a+c>b+d ( )10.若a>b, c>d ,则a-c>b-d ( )×××××√√(1)由xmy的条件是( )
A、m≥0 B、m≤0 C、m＞0 D、m＜0
(2)若 mx< m,且x>1,则应为( )
A、m<0 B、m>0 C、m≤0 D、m≥0
(3)若m是有理数,则-7m与3m的大小关系应是( )
A、-7m<3m B、-7m>3m C、-7m≤3m D、不能确定DAD看谁做得对又快例1. 根据不等式的性质,把下列不等式化成 x>a 或 x -5（4）–4x > 3
思考探索1、若不等式（a-1）x>a-1的解集是x<1,求a应满足什么条件？
思考探索2、已知不等式3x-a 0的正整数解是 1，2，3，求a的范围.利用不等式的性质解下列不等式你知道了什么？请 你 谈 收 获学会了什么？发现了什么？谢谢同学们！再见！