(苏科版八年级上)数学:第四章数量、位置的变化复习学案
文档属性
| 名称 | (苏科版八年级上)数学:第四章数量、位置的变化复习学案 |  | |
| 格式 | rar | ||
| 文件大小 | 235.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-14 18:45:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第四章数量、位置的变化
一、知识点:
1、数量的变化:
⑴生活中处处有变化的数量关系,并且这些变化的数量之间往往有一定的联系;感受用变化的观点分析数字信息的重要意义。
⑵实际问题中的数量常常会发生变化,表示这种变化通常有3种各具特色的表达方式——表格、图形、式子,可根据实际情况灵活选用。
2、位置的变化:
现实生活中,人们既关心事物的数量变化,也关心事物的位置变化,如行驶中的车辆、飞行中的火箭、航行中的船只、移动中的台风等位置的变化。
3、平面直角坐标系:
⑴有关概念:平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称直角坐标系。
水平方向的数轴称为x轴或横轴;竖直方向的数轴称为y轴或纵轴。它们统称坐标轴。公共原点O称为坐标原点。
⑵确定点的位置(点坐标)
①若平面内有一点P(如图),我们应该如何确定它的位置?
(过点P分别作x、y轴的垂线,将垂足对应的数组合起来形成一对有序实数,这样的有序实数对叫做点的坐标,可表示为P(a,b)
②若已知点Q的坐标为(m,n),该如何确定点Q的位置?
(分别过x、y轴上表示m、n的点作x、y轴的垂线,两线的交点即为点Q)
例:分别在平面直角坐标系内确定点A(3,2)、B(2,3)的位置。21世纪教育网
4、点坐标的特征:
⑴四个象限内点坐标的特征:
两条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别记作第一、二、三、四象限。
⑵数轴上点坐标的特征:
x轴上的点的纵坐标为0,可表示为(a,0);
y轴上的点的横坐标为0,可表示为(0,b)。
⑶象限角平分线上点坐标的特征:
第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a)。
⑷对称点坐标的特征:
P(a,b)关于x轴对称的点的坐标为(a,-b);
P(a,b)关于y轴对称的点的坐标为(-a,b);
P(a,b)关于原点对称的点的坐标为(-a,-b)。21世纪教育网
二、举例:
例1:研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮服的施用量有如下关系:
氮肥施用量/(千克/公顷) 0 34 67 101 135 202 259 336 404 471
土豆产量/(吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75[来源:21世纪教育网]
(1)上表反映了哪两个变量之间的关系?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
例2:温度的变化,是人们经常谈论的话题,请你根据下图,与同伴交流讨论某地某天的温度变化的情况。
(1) 上午9时的温度是多少?12时呢?
(2) 这一天的最高温度是多少?是在几时达到的?最低温度是多少?
(3) 这一天的的温差是多少?从最低温度到最高温度经过了多少时间?
(4) 在什么时间范围内温度在上升?在什么时间范围内温度在下降?
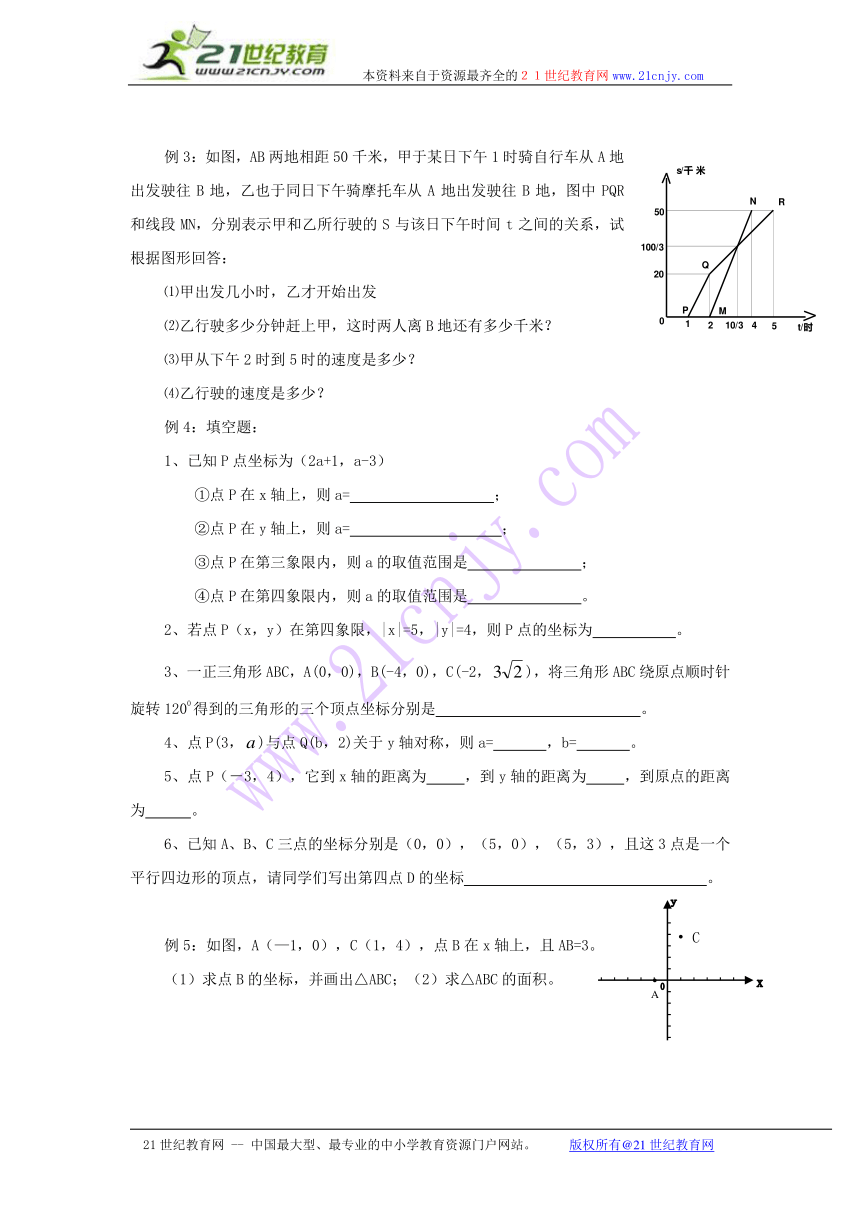
例3:如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
⑴甲出发几小时,乙才开始出发
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
例4:填空题:
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 。
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 。
3、一正三角形ABC,A(0,0),B(-4,0),C(-2,),将三角形ABC绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是 。
4、点P(3,)与点Q(b,2)关于y轴对称,则a= ,b= 。
5、点P(-3,4),它到x轴的距离为 ,到y轴的距离为 ,到原点的距离为 。[来源:21世纪教育网]
6、已知A、B、C三点的坐标分别是(0,0),(5,0),(5,3),且这3点是一个平行四边形的顶点,请同学们写出第四点D的坐标 。
例5:如图,A(—1,0),C(1,4),点B在x轴上,且AB=3。
(1)求点B的坐标,并画出△ABC;(2)求△ABC的面积。
例6:已知两点A(0,2),B(4,1),点P是x轴上的一点,求P A+PB的最小值。
1、 例7:如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,
AB=6,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标。
例8:如图表示甲、乙两名选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
(1)求比赛开始多少分钟时,两人第一次相遇;
(2)求这次比赛的全程是多少千米;
(3)求比赛开始多少分钟时,两人第二次相遇。
三、作业:
数量x(g) 售价c(元)
100 0.9+0.1
200 1.8+0.1
300 2.7+0.1
400 3.6+0.1
1、商店出售一种瓜子,数量x(g)与售价c(元)之间的关系如下表:
表中售价栏中的0.1是塑料袋的价钱。
(1)写出售价c(元)与数量x(g)之间的关系式是 ;
(2)当数量由1kg变化到3kg时,售价的变化范围是 元。
2、 如图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的关系,根据图中提供的信息,求:①汽车共行驶了多少千米?②汽车在行驶途中停留了几小时?③汽车在整个行驶过程中的平均速度是多少?④汽车自出发后3小时至4.5小时之间行驶的速度是多少?
3、 已知平面直角坐标系中两点A(x,1)、B(一5,y)
(1)若点A、B关于x轴对称,则x=____,y=____;
(2)若点A、B关于y轴对称,则x=____,y=_____;
(3)若点A、B关于原点对称,则x=____,y=_____
4、已知点P(2m一5,m一1),当m为何值时:
(1)点P在二、四象限的角平分线上;
(2)点P在一、三象限的角平分线上
5、如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,AB与y轴的交点坐标D为(0,4)。求A、B的坐标。
6、如图,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限,OA与
x轴的夹角为30°。求A、B、C的坐标。
O
x
y
4
2
3
1
4
3
2
1
-2
-3
-1
-4
-3
-2
-1
-4
P(a,b)
·
a
b
O
x
y
第四象限
第三象限
第二象限
第一象限
A
C
y
x
O
E
D
C
M
B
A
·
y
x
O
D
B
A
y
x
O
C
B
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第四章数量、位置的变化
一、知识点:
1、数量的变化:
⑴生活中处处有变化的数量关系,并且这些变化的数量之间往往有一定的联系;感受用变化的观点分析数字信息的重要意义。
⑵实际问题中的数量常常会发生变化,表示这种变化通常有3种各具特色的表达方式——表格、图形、式子,可根据实际情况灵活选用。
2、位置的变化:
现实生活中,人们既关心事物的数量变化,也关心事物的位置变化,如行驶中的车辆、飞行中的火箭、航行中的船只、移动中的台风等位置的变化。
3、平面直角坐标系:
⑴有关概念:平面上有公共原点且互相垂直的2条数轴构成平面直角坐标系,简称直角坐标系。
水平方向的数轴称为x轴或横轴;竖直方向的数轴称为y轴或纵轴。它们统称坐标轴。公共原点O称为坐标原点。
⑵确定点的位置(点坐标)
①若平面内有一点P(如图),我们应该如何确定它的位置?
(过点P分别作x、y轴的垂线,将垂足对应的数组合起来形成一对有序实数,这样的有序实数对叫做点的坐标,可表示为P(a,b)
②若已知点Q的坐标为(m,n),该如何确定点Q的位置?
(分别过x、y轴上表示m、n的点作x、y轴的垂线,两线的交点即为点Q)
例:分别在平面直角坐标系内确定点A(3,2)、B(2,3)的位置。21世纪教育网
4、点坐标的特征:
⑴四个象限内点坐标的特征:
两条坐标轴将平面分成4个区域称为象限,按逆时针顺序分别记作第一、二、三、四象限。
⑵数轴上点坐标的特征:
x轴上的点的纵坐标为0,可表示为(a,0);
y轴上的点的横坐标为0,可表示为(0,b)。
⑶象限角平分线上点坐标的特征:
第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a)。
⑷对称点坐标的特征:
P(a,b)关于x轴对称的点的坐标为(a,-b);
P(a,b)关于y轴对称的点的坐标为(-a,b);
P(a,b)关于原点对称的点的坐标为(-a,-b)。21世纪教育网
二、举例:
例1:研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮服的施用量有如下关系:
氮肥施用量/(千克/公顷) 0 34 67 101 135 202 259 336 404 471
土豆产量/(吨/公顷) 15.18 21.36 25.72 32.29 34.03 39.45 43.15 43.46 40.83 30.75[来源:21世纪教育网]
(1)上表反映了哪两个变量之间的关系?
(2)当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施氮肥呢?
(3)根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
例2:温度的变化,是人们经常谈论的话题,请你根据下图,与同伴交流讨论某地某天的温度变化的情况。
(1) 上午9时的温度是多少?12时呢?
(2) 这一天的最高温度是多少?是在几时达到的?最低温度是多少?
(3) 这一天的的温差是多少?从最低温度到最高温度经过了多少时间?
(4) 在什么时间范围内温度在上升?在什么时间范围内温度在下降?
例3:如图,AB两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车从A地出发驶往B地,图中PQR和线段MN,分别表示甲和乙所行驶的S与该日下午时间t之间的关系,试根据图形回答:
⑴甲出发几小时,乙才开始出发
⑵乙行驶多少分钟赶上甲,这时两人离B地还有多少千米?
⑶甲从下午2时到5时的速度是多少?
⑷乙行驶的速度是多少?
例4:填空题:
1、已知P点坐标为(2a+1,a-3)
①点P在x轴上,则a= ;
②点P在y轴上,则a= ;
③点P在第三象限内,则a的取值范围是 ;
④点P在第四象限内,则a的取值范围是 。
2、若点P(x,y)在第四象限,|x|=5,|y|=4,则P点的坐标为 。
3、一正三角形ABC,A(0,0),B(-4,0),C(-2,),将三角形ABC绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是 。
4、点P(3,)与点Q(b,2)关于y轴对称,则a= ,b= 。
5、点P(-3,4),它到x轴的距离为 ,到y轴的距离为 ,到原点的距离为 。[来源:21世纪教育网]
6、已知A、B、C三点的坐标分别是(0,0),(5,0),(5,3),且这3点是一个平行四边形的顶点,请同学们写出第四点D的坐标 。
例5:如图,A(—1,0),C(1,4),点B在x轴上,且AB=3。
(1)求点B的坐标,并画出△ABC;(2)求△ABC的面积。
例6:已知两点A(0,2),B(4,1),点P是x轴上的一点,求P A+PB的最小值。
1、 例7:如图,已知ΔABC在坐标平面内的顶点C(2,0),∠ACB=90°,∠B=30°,
AB=6,∠BCD=45°。①求A、B的坐标;②求AB中点M的坐标。
例8:如图表示甲、乙两名选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图象(全程),根据图象回答下列问题:
(1)求比赛开始多少分钟时,两人第一次相遇;
(2)求这次比赛的全程是多少千米;
(3)求比赛开始多少分钟时,两人第二次相遇。
三、作业:
数量x(g) 售价c(元)
100 0.9+0.1
200 1.8+0.1
300 2.7+0.1
400 3.6+0.1
1、商店出售一种瓜子,数量x(g)与售价c(元)之间的关系如下表:
表中售价栏中的0.1是塑料袋的价钱。
(1)写出售价c(元)与数量x(g)之间的关系式是 ;
(2)当数量由1kg变化到3kg时,售价的变化范围是 元。
2、 如图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的关系,根据图中提供的信息,求:①汽车共行驶了多少千米?②汽车在行驶途中停留了几小时?③汽车在整个行驶过程中的平均速度是多少?④汽车自出发后3小时至4.5小时之间行驶的速度是多少?
3、 已知平面直角坐标系中两点A(x,1)、B(一5,y)
(1)若点A、B关于x轴对称,则x=____,y=____;
(2)若点A、B关于y轴对称,则x=____,y=_____;
(3)若点A、B关于原点对称,则x=____,y=_____
4、已知点P(2m一5,m一1),当m为何值时:
(1)点P在二、四象限的角平分线上;
(2)点P在一、三象限的角平分线上
5、如图,直角三角形OAB中,∠AOB=90°,∠A=60°∠xOA=30°,AB与y轴的交点坐标D为(0,4)。求A、B的坐标。
6、如图,已知边长为1的正方形OABC在直角坐标系中,A、B两点在第一象限,OA与
x轴的夹角为30°。求A、B、C的坐标。
O
x
y
4
2
3
1
4
3
2
1
-2
-3
-1
-4
-3
-2
-1
-4
P(a,b)
·
a
b
O
x
y
第四象限
第三象限
第二象限
第一象限
A
C
y
x
O
E
D
C
M
B
A
·
y
x
O
D
B
A
y
x
O
C
B
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
