(苏科版八年级上)数学:3.4平行四边形课件(1)
文档属性
| 名称 | (苏科版八年级上)数学:3.4平行四边形课件(1) |  | |
| 格式 | rar | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-14 18:46:00 | ||
图片预览








文档简介
课件32张PPT。 在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
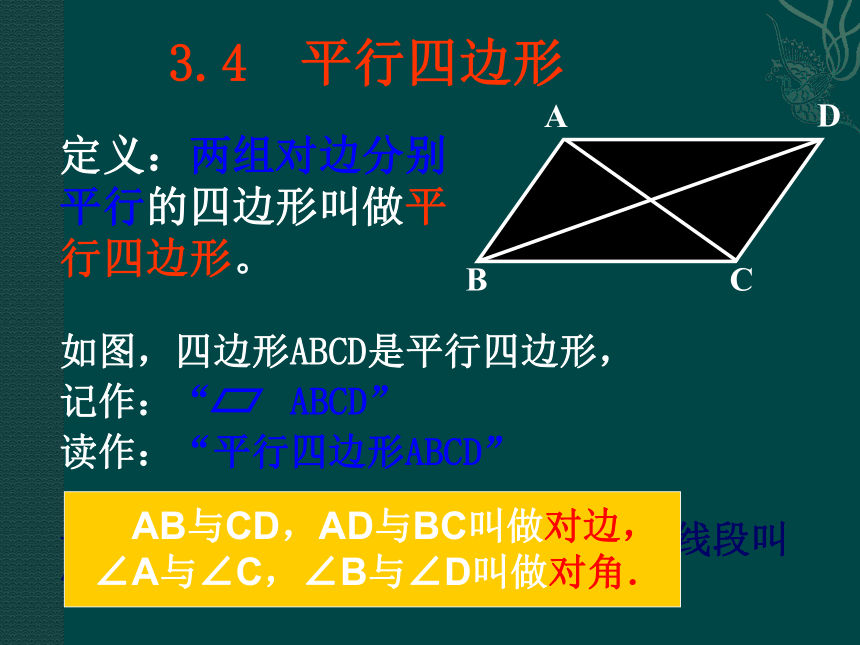
把一个平面图形绕某一点旋转1800,如果它能够与原来图形重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.中心对称图形比如:这些图片中有你熟悉的图形吗?定义:两组对边分别平行的四边形叫做平行四边形。平行四边形不相邻的两个顶点连成的线段叫它的对角线。BADC3.4 平行四边形如图,四边形ABCD是平行四边形,
记作:“ ABCD”
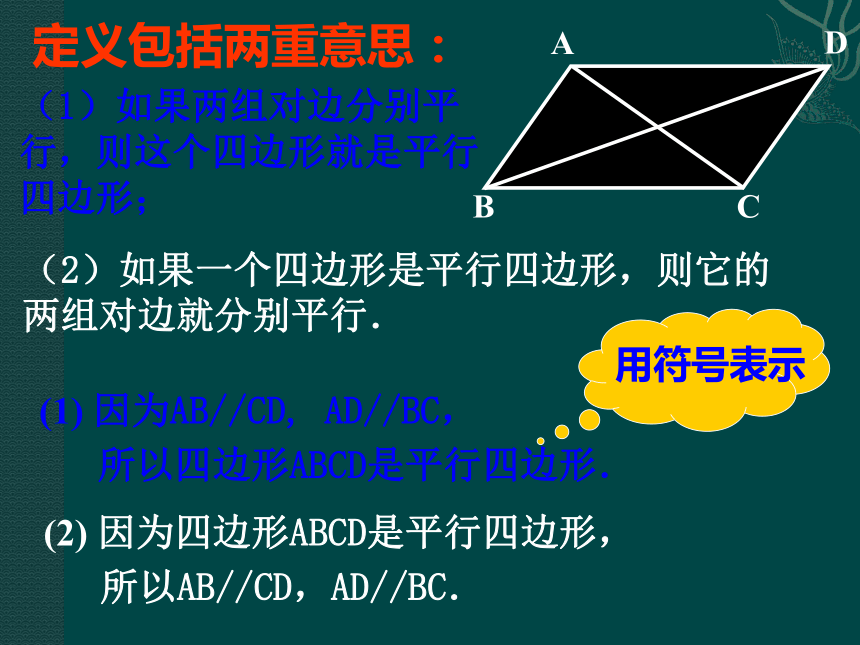
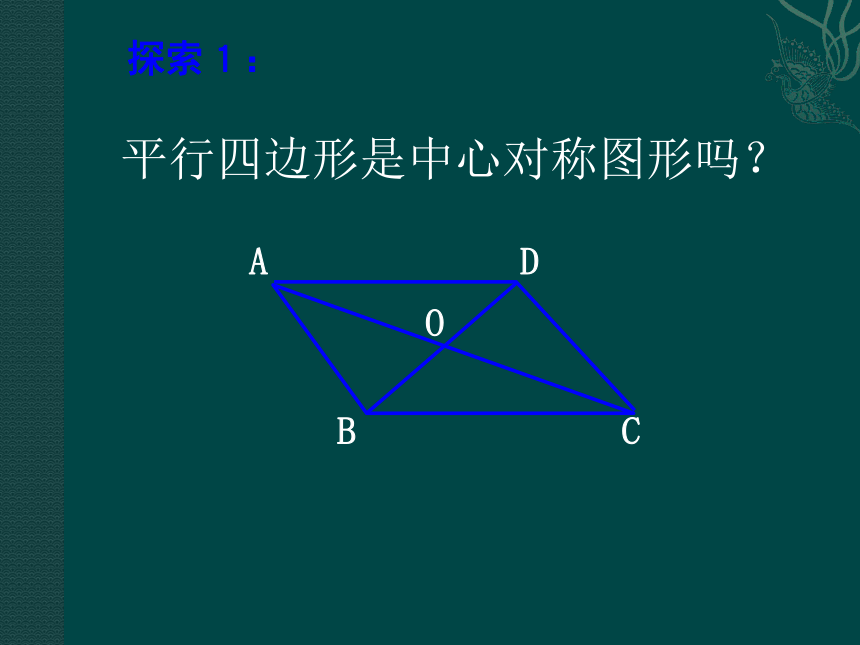
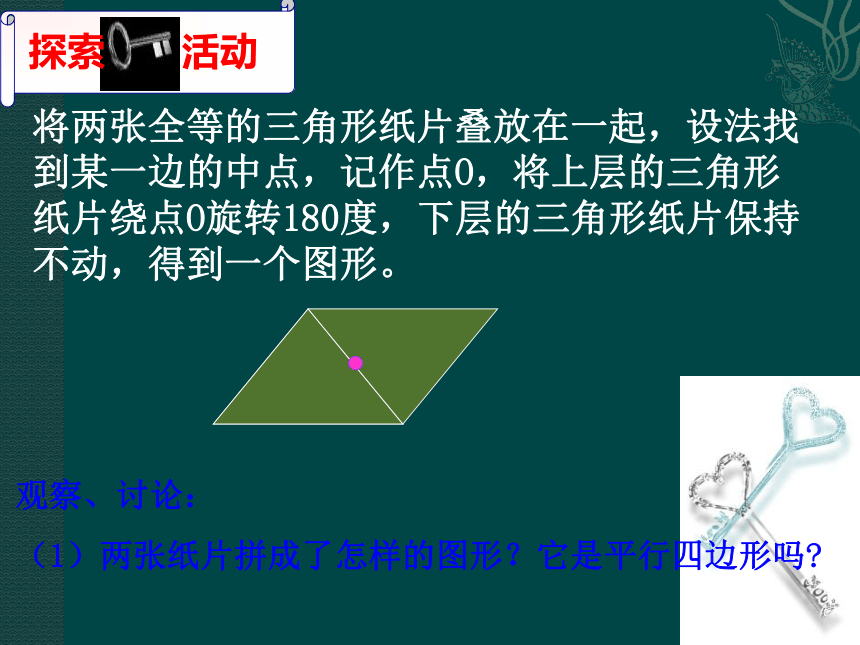
读作:“平行四边形ABCD”(1)如果两组对边分别平行,则这个四边形就是平行四边形;(2)如果一个四边形是平行四边形,则它的 两组对边就分别平行.(1) 因为AB//CD, AD//BC,所以四边形ABCD是平行四边形.(2) 因为四边形ABCD是平行四边形,所以AB//CD,AD//BC.定义包括两重意思:平行四边形是中心对称图形吗?探索1: 请同学合作讨论,利用一个三角形绕一个定点旋转180°,能得到一个平行四边形吗?你们是怎么做的?请派小组代表展示你们的成果。 实验:将两张全等的三角形纸片叠放在一起,设法找到某一边的中点,记作点O,将上层的三角形纸片绕点O旋转180度,下层的三角形纸片保持不动,得到一个图形。观察、讨论:
(1)两张纸片拼成了怎样的图形?它是平行四边形吗?探索 活动由△ABC绕点O旋转180°得到△CDA,可知:
△ABC≌ △CDA. 因此∠1= ∠2, ∠3= ∠4,
从而AB∥CD、AD ∥ CB。理由是:内错角相等,两直线平行。
所以,四边形ABCD是平行四边形.理由是:两组对边分别平行的四边形叫做平行四边形。ABCDO1.四边形ABCD是平行四边形吗?1234ABCDO2.平行四边形ABCD是中心对称图形吗?1234交流讨论这个图形中的△CDA可以看作是△ABC绕点O旋转180°得到的,因此,四边形ABCD是中心对称图形,点O是它的对称中心.BACD演示:平行四边形是中心对称图形平行四边形是一个中心对称图形。对角线的交点是它的对称中心。(D)(A)(B)(C)O平行四边形的边、角、对角线还有哪些特征?探索2:BACD演示:平行四边形的性质平行四边形的对边相等。平行四边形的对角线互相平分。 (D)(A)(B)(C)O平行四边形的对角相等。几何语言:因为四边形ABCD是平行四边形所以AB=CD, AD=BC平行四边形的对边相等.理由是:平行四边形的对边相等.
平行四边形的对角相等.因为四边形ABCD是平行四边形,所以∠A=∠C,∠B=∠D.理由是:平行四边形的对角相等.
因为四边形ABCD是平行四边形所以OA=OC, OB=OD.平行四边形的对角线互相平分.理由是:平行四边形的对角线互相平分.
帮帮忙! 学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢?ABCA’B’C’例题:如图,A’B’∥AB,B’C’∥BC,C’A’∥CA,图中有几个平行四边形?将它们表示出来,并说明理由。解:图中共有3个平行四边形: □ABCB’、□ C’BCA、□ABA’C。因为A’B’∥AB,B’C’∥BC
所以四边形ABCB’是平行四边形。
理由是:两组对边分别平行的四边形是平行四边形。同样可以得到:四边形C’BCA、四边形ABA’C也是平行四边形。如图,A’B’∥AB,B’C’∥BC,C’A’∥CA.上图中,AB与B’C, ∠ABC与∠B’相等吗? 为什么?你还能得到哪些结论?B1.如图, ABCD中,∠B=50°因为四边形ABCD是平行四边形
所以AD∥ BC
理由是:平行四边形的对边互相平行
所以∠A+∠B=180°(两直线平行,同旁内角互补)
即∠A=180°- ∠B =130 °
所以∠C =∠A =130° .
理由是:平行四边形的对角相等.
练兵场:因为四边形ABCD是平行四边形,
所以∠ D =∠ B =50° .
理由是:平行四边形的对角相等.
你能知道什么呢?解:在平行四边形ABCD中,已知
∠A+∠C=260°,你能很快求出 ∠A、∠B、∠C、∠D的度数吗?若将已知条件改成:练兵场:2、如图,□ABCD的对角线相交于点O,BC=7cm,BD=10cm,AC=6cm,你还能知道什么?练兵场:解: △AOB的周长是15 cm.因为四边形ABCD是平行四边形,所以OA=OC=3 cm , OB=OD=5cm.理由是:平行四边形的对角线互相平分.又因为AD=BC= 7cm,理由是:平行四边形的对边相等.所以△AOD的周长= 15 cm.3.如图,口ABCD中,点E在边AD上,将△ABE 沿BE折叠,点A正好落在CD上的点F.F练兵场:你能求出CF的长吗?已知△FDE的周长为8,△FCB的周长为22.你能求出什么?口ABCD的周长是30.CF的长是7.请你画一条直线,将已知的平行四边形分成面积相等的两部分。你有多少种方法?有无数种画法,这些直线都经过对角线的交点回归生活: 课后思考:如果是分成面积相等的四部分呢?
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S、S1、S2之间有什么样的关系,并说明理由.
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.平行四边形平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等 平行四边形的对角线
互相平分说说你的收获(中心对称图形,对称中心是对角线的交点) 如图,村子里有一四边形的池塘,在它的四个角的顶点A、B、C、D处均种了一棵大核桃树。村子准备开挖池塘建养鱼塘,想使池塘的面积扩大1倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一构想?若能,请你画出图形;若不能,请说明理由。
课后思考题
——毕达哥拉斯
把一个平面图形绕某一点旋转1800,如果它能够与原来图形重合,那么这个图形叫做中心对称图形.这个点就是它的对称中心.中心对称图形比如:这些图片中有你熟悉的图形吗?定义:两组对边分别平行的四边形叫做平行四边形。平行四边形不相邻的两个顶点连成的线段叫它的对角线。BADC3.4 平行四边形如图,四边形ABCD是平行四边形,
记作:“ ABCD”
读作:“平行四边形ABCD”(1)如果两组对边分别平行,则这个四边形就是平行四边形;(2)如果一个四边形是平行四边形,则它的 两组对边就分别平行.(1) 因为AB//CD, AD//BC,所以四边形ABCD是平行四边形.(2) 因为四边形ABCD是平行四边形,所以AB//CD,AD//BC.定义包括两重意思:平行四边形是中心对称图形吗?探索1: 请同学合作讨论,利用一个三角形绕一个定点旋转180°,能得到一个平行四边形吗?你们是怎么做的?请派小组代表展示你们的成果。 实验:将两张全等的三角形纸片叠放在一起,设法找到某一边的中点,记作点O,将上层的三角形纸片绕点O旋转180度,下层的三角形纸片保持不动,得到一个图形。观察、讨论:
(1)两张纸片拼成了怎样的图形?它是平行四边形吗?探索 活动由△ABC绕点O旋转180°得到△CDA,可知:
△ABC≌ △CDA. 因此∠1= ∠2, ∠3= ∠4,
从而AB∥CD、AD ∥ CB。理由是:内错角相等,两直线平行。
所以,四边形ABCD是平行四边形.理由是:两组对边分别平行的四边形叫做平行四边形。ABCDO1.四边形ABCD是平行四边形吗?1234ABCDO2.平行四边形ABCD是中心对称图形吗?1234交流讨论这个图形中的△CDA可以看作是△ABC绕点O旋转180°得到的,因此,四边形ABCD是中心对称图形,点O是它的对称中心.BACD演示:平行四边形是中心对称图形平行四边形是一个中心对称图形。对角线的交点是它的对称中心。(D)(A)(B)(C)O平行四边形的边、角、对角线还有哪些特征?探索2:BACD演示:平行四边形的性质平行四边形的对边相等。平行四边形的对角线互相平分。 (D)(A)(B)(C)O平行四边形的对角相等。几何语言:因为四边形ABCD是平行四边形所以AB=CD, AD=BC平行四边形的对边相等.理由是:平行四边形的对边相等.
平行四边形的对角相等.因为四边形ABCD是平行四边形,所以∠A=∠C,∠B=∠D.理由是:平行四边形的对角相等.
因为四边形ABCD是平行四边形所以OA=OC, OB=OD.平行四边形的对角线互相平分.理由是:平行四边形的对角线互相平分.
帮帮忙! 学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢?ABCA’B’C’例题:如图,A’B’∥AB,B’C’∥BC,C’A’∥CA,图中有几个平行四边形?将它们表示出来,并说明理由。解:图中共有3个平行四边形: □ABCB’、□ C’BCA、□ABA’C。因为A’B’∥AB,B’C’∥BC
所以四边形ABCB’是平行四边形。
理由是:两组对边分别平行的四边形是平行四边形。同样可以得到:四边形C’BCA、四边形ABA’C也是平行四边形。如图,A’B’∥AB,B’C’∥BC,C’A’∥CA.上图中,AB与B’C, ∠ABC与∠B’相等吗? 为什么?你还能得到哪些结论?B1.如图, ABCD中,∠B=50°因为四边形ABCD是平行四边形
所以AD∥ BC
理由是:平行四边形的对边互相平行
所以∠A+∠B=180°(两直线平行,同旁内角互补)
即∠A=180°- ∠B =130 °
所以∠C =∠A =130° .
理由是:平行四边形的对角相等.
练兵场:因为四边形ABCD是平行四边形,
所以∠ D =∠ B =50° .
理由是:平行四边形的对角相等.
你能知道什么呢?解:在平行四边形ABCD中,已知
∠A+∠C=260°,你能很快求出 ∠A、∠B、∠C、∠D的度数吗?若将已知条件改成:练兵场:2、如图,□ABCD的对角线相交于点O,BC=7cm,BD=10cm,AC=6cm,你还能知道什么?练兵场:解: △AOB的周长是15 cm.因为四边形ABCD是平行四边形,所以OA=OC=3 cm , OB=OD=5cm.理由是:平行四边形的对角线互相平分.又因为AD=BC= 7cm,理由是:平行四边形的对边相等.所以△AOD的周长= 15 cm.3.如图,口ABCD中,点E在边AD上,将△ABE 沿BE折叠,点A正好落在CD上的点F.F练兵场:你能求出CF的长吗?已知△FDE的周长为8,△FCB的周长为22.你能求出什么?口ABCD的周长是30.CF的长是7.请你画一条直线,将已知的平行四边形分成面积相等的两部分。你有多少种方法?有无数种画法,这些直线都经过对角线的交点回归生活: 课后思考:如果是分成面积相等的四部分呢?
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S、S1、S2之间有什么样的关系,并说明理由.
如图,M是 ABCD边AD上任一点,若 △CBM的面积为S, △ABM的面积为S1, △CDM的面积为S2,请猜测一下S,S1,S2之间有什么样的关系,并说明理由.平行四边形平行四边形的对边平行平行四边形的对边相等平行四边形的对角相等 平行四边形的对角线
互相平分说说你的收获(中心对称图形,对称中心是对角线的交点) 如图,村子里有一四边形的池塘,在它的四个角的顶点A、B、C、D处均种了一棵大核桃树。村子准备开挖池塘建养鱼塘,想使池塘的面积扩大1倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形的形状,请问能否实现这一构想?若能,请你画出图形;若不能,请说明理由。
课后思考题
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
