2.3直线与平面垂直的判定以及性质周练(无答案)
文档属性
| 名称 | 2.3直线与平面垂直的判定以及性质周练(无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 89.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-12-16 21:48:00 | ||
图片预览

文档简介
2.3直线、平面垂直的判定及其性质
2010-12-11
例1:线线垂直线面垂直
已知:空间四边形,,,求证:
例2:线面成角(斜线与射影的夹角)
已知是矩形,平面,,,为的中点.
求直线与平面所成的角.
例3:二面角的大小(能够作出二面角的平面角)
如图,在四面体ABCD中,△ABD、△ACD、△BCD、△ABC都全等,且,BC=2,求以BC为棱、以面BCD和面BCA为面的二面角的大小.
例4:面面垂直的判定(线线垂直线面垂直面面垂直)
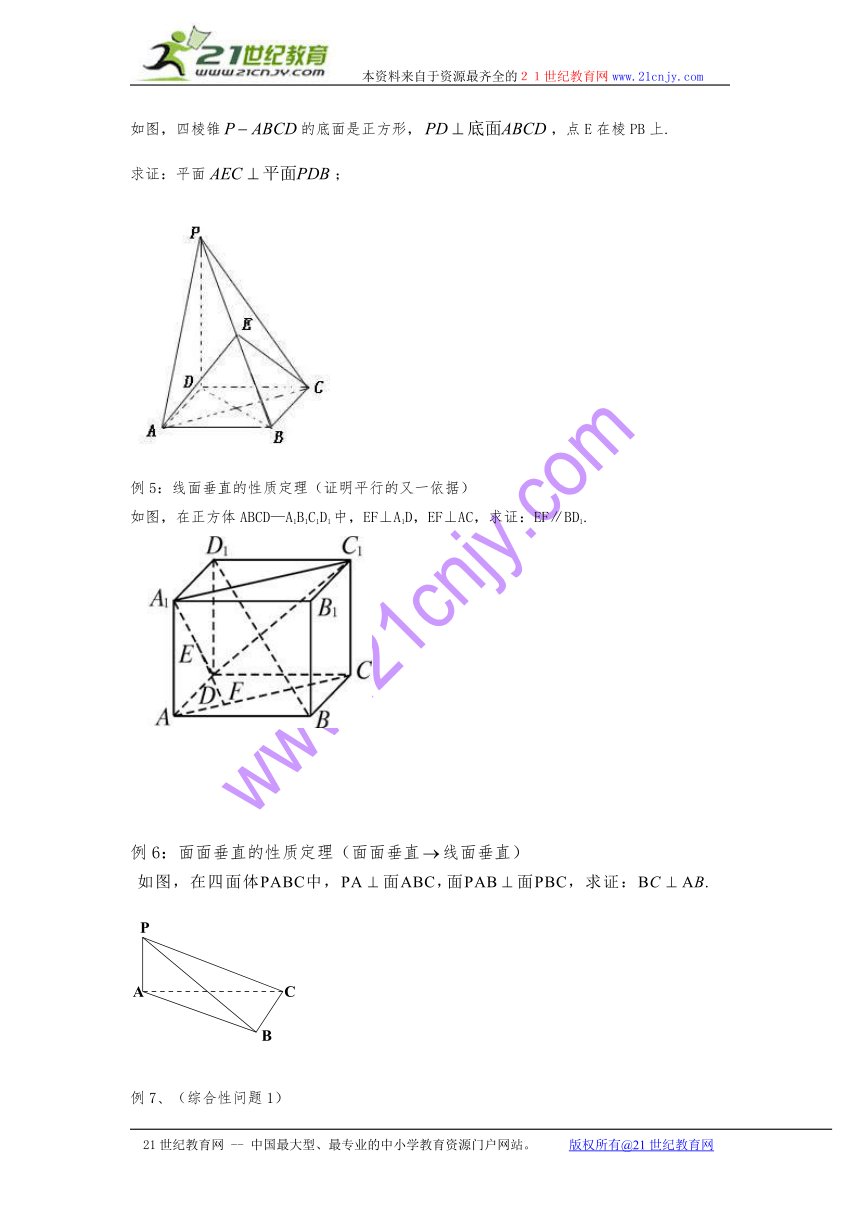
如图,四棱锥的底面是正方形,,点E在棱PB上.
求证:平面;
例5:线面垂直的性质定理(证明平行的又一依据)
如图,在正方体ABCD—A1B1C1D1中,EF⊥A1D,EF⊥AC,求证:EF∥BD1.
例6:面面垂直的性质定理(面面垂直线面垂直)
例7、(综合性问题1)
18.如图,在正方体中,是的中点.
(1)求证:平面
(2)求证:平面平面.
例8、(综合性问题2)
如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
1、一条直线与平面(的一条垂线垂直,则直线与平面(的位置关系是 ( )
A、(( B、⊥( C、∥( D、((或∥(
2、直线l⊥平面(,①若直线m⊥l,则m∥(;②若m⊥(,则m∥l;
③若m∥(,则m⊥l④若m∥l,则m⊥(,上述判断正确的是( )
A、①②③ B、②③④ C、①③④ D、②④
3、P是△ABC所在平面α外一点,且P到△ABC三边的距离都相等,PO⊥α于O,
O在△ABC内,则O是△ABC的( )
A、外心 B、内心 C、重心 D、垂心
4、正方体ABCD-A1B 1C1D1中与AD1垂直的平面是 ( )
A、平面DD1C1C B、平面A1DB1 C、平面A1B1C1D1 D、平面A1DB
5、菱形ABCD在平面内,PC⊥,则PA与BD的位置关系是 ( )
A、平行 B、相交 C、垂直相交 D、异面垂直
6、下列命题正确的是 ( )
(A) (B) (C) (D)
7、(1)过直线外一点作直线的垂线有 条;垂面有 个;平行线有 条;平行平面有 个;
(2)过平面外一点作该平面的垂线有 条;垂面有 个;平行线有 条;平行平面有 个;
(3)过平面α的一条斜线可作 个平面与平面α垂直;
(4)过平面α的一条平行线可作 个平面与平面α垂直。
8、点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( ) (A)内心 (B)外心 (C)重心 (D)垂心
9、P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是(??? )
A.平面PAB与平面PBC、平面PAD都垂直
B.它们两两都垂直
C.平面PAB与平面PBC垂直、与平面PAD不垂直
D.平面PAB与平面PBC、平面PAD都不垂直
10、线段AB的长等于它在平面α内射影长的2倍,则AB所在直线与平面α所成的角为( )
A.30°???????????? B.45°???????????? C.60°???????????? D.120°
2010-12-11
例1:线线垂直线面垂直
已知:空间四边形,,,求证:
例2:线面成角(斜线与射影的夹角)
已知是矩形,平面,,,为的中点.
求直线与平面所成的角.
例3:二面角的大小(能够作出二面角的平面角)
如图,在四面体ABCD中,△ABD、△ACD、△BCD、△ABC都全等,且,BC=2,求以BC为棱、以面BCD和面BCA为面的二面角的大小.
例4:面面垂直的判定(线线垂直线面垂直面面垂直)
如图,四棱锥的底面是正方形,,点E在棱PB上.
求证:平面;
例5:线面垂直的性质定理(证明平行的又一依据)
如图,在正方体ABCD—A1B1C1D1中,EF⊥A1D,EF⊥AC,求证:EF∥BD1.
例6:面面垂直的性质定理(面面垂直线面垂直)
例7、(综合性问题1)
18.如图,在正方体中,是的中点.
(1)求证:平面
(2)求证:平面平面.
例8、(综合性问题2)
如图,在底面为平行四边形的四棱锥中,,平面,且,点是的中点.
(Ⅰ)求证:;
(Ⅱ)求证:平面;
(Ⅲ)求二面角的大小.
1、一条直线与平面(的一条垂线垂直,则直线与平面(的位置关系是 ( )
A、(( B、⊥( C、∥( D、((或∥(
2、直线l⊥平面(,①若直线m⊥l,则m∥(;②若m⊥(,则m∥l;
③若m∥(,则m⊥l④若m∥l,则m⊥(,上述判断正确的是( )
A、①②③ B、②③④ C、①③④ D、②④
3、P是△ABC所在平面α外一点,且P到△ABC三边的距离都相等,PO⊥α于O,
O在△ABC内,则O是△ABC的( )
A、外心 B、内心 C、重心 D、垂心
4、正方体ABCD-A1B 1C1D1中与AD1垂直的平面是 ( )
A、平面DD1C1C B、平面A1DB1 C、平面A1B1C1D1 D、平面A1DB
5、菱形ABCD在平面内,PC⊥,则PA与BD的位置关系是 ( )
A、平行 B、相交 C、垂直相交 D、异面垂直
6、下列命题正确的是 ( )
(A) (B) (C) (D)
7、(1)过直线外一点作直线的垂线有 条;垂面有 个;平行线有 条;平行平面有 个;
(2)过平面外一点作该平面的垂线有 条;垂面有 个;平行线有 条;平行平面有 个;
(3)过平面α的一条斜线可作 个平面与平面α垂直;
(4)过平面α的一条平行线可作 个平面与平面α垂直。
8、点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( ) (A)内心 (B)外心 (C)重心 (D)垂心
9、P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是(??? )
A.平面PAB与平面PBC、平面PAD都垂直
B.它们两两都垂直
C.平面PAB与平面PBC垂直、与平面PAD不垂直
D.平面PAB与平面PBC、平面PAD都不垂直
10、线段AB的长等于它在平面α内射影长的2倍,则AB所在直线与平面α所成的角为( )
A.30°???????????? B.45°???????????? C.60°???????????? D.120°
