导数的几何意义
图片预览





文档简介
课件12张PPT。3.1.3导数及其几何意义我们把物体在某一时刻的速度称为瞬时速度.从函数y=f(x)在x=x0处的瞬时变化率是: 一、知识回顾:从函数y=f(x)在x=x0处的导数是一个确定的数,当x变化时,f(x)便是x的一个函数,我们称它为f(x)的导函数(简称导数)即: 二、导函数的定义由导数的意义可知,求函数y=f(x)导数的基本方法是:注意:这里的增量不是一般意义上的增量,它可正也可负.
自变量的增量Δx的形式是多样的,但不论Δx选择
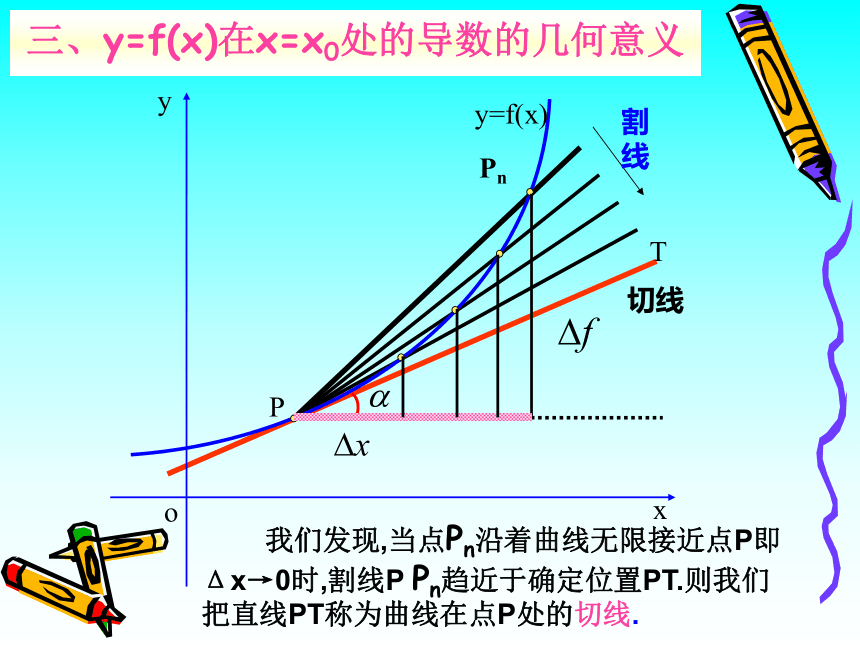
哪种形式, Δy也必须选择与之相对应的形式.类比例1:求函数 的导数。 练习:求下列函数的导数。 PPn割线切线T三、y=f(x)在x=x0处的导数的几何意义 我们发现,当点Pn沿着曲线无限接近点P即Δx→0时,割线P Pn趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.问题:割线PPn的斜率kn与切线PT的斜率k
有什么关系?割线PPn的斜率:设相对于 的增加量为 , ,则 当点Pn无限趋近于点P即Δx→0时,
kn无限趋近于切线PT的斜率k.那么当Δx→0时,割线P Pn的斜率,称为曲线在点P处的切线的斜率.即:这个概念: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.因此,函数f(x)在x=x0处的
导数就是切线PT的斜率.
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
例2:求曲线y=f(x)=x2在点P(1,2)处的切线方程.y-2=2(x-1)即y=2x.练习:
求曲线f(x)= 在点P(1,1)处的切线方程.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即1.求切线方程的步骤:小结: 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念。
2.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态。
自变量的增量Δx的形式是多样的,但不论Δx选择
哪种形式, Δy也必须选择与之相对应的形式.类比例1:求函数 的导数。 练习:求下列函数的导数。 PPn割线切线T三、y=f(x)在x=x0处的导数的几何意义 我们发现,当点Pn沿着曲线无限接近点P即Δx→0时,割线P Pn趋近于确定位置PT.则我们把直线PT称为曲线在点P处的切线.问题:割线PPn的斜率kn与切线PT的斜率k
有什么关系?割线PPn的斜率:设相对于 的增加量为 , ,则 当点Pn无限趋近于点P即Δx→0时,
kn无限趋近于切线PT的斜率k.那么当Δx→0时,割线P Pn的斜率,称为曲线在点P处的切线的斜率.即:这个概念: ①提供了求曲线上某点切线的斜率的一种方法;
②切线斜率的本质——函数在x=x0处的导数.因此,函数f(x)在x=x0处的
导数就是切线PT的斜率.
圆的切线定义并不适用于一般的曲线。
通过逼近的方法,将割线趋于的确定位置的直线定义为切线(交点可能不惟一)适用于各种曲线。所以,这种定义才真正反映了切线的直观本质。
例2:求曲线y=f(x)=x2在点P(1,2)处的切线方程.y-2=2(x-1)即y=2x.练习:
求曲线f(x)= 在点P(1,1)处的切线方程.(1)求出函数在点x0处的变化率 ,得到曲线
在点(x0,f(x0))的切线的斜率。(2)根据直线方程的点斜式写出切线方程,即1.求切线方程的步骤:小结: 无限逼近的极限思想是建立导数概念、用导数定义求 函数的导数的基本思想,丢掉极限思想就无法理解导 数概念。
2.导数是从众多实际问题中抽象出来的具有相同的数
学表达式的一个重要概念,要从它的几何意义和物
理意义了认识这一概念的实质,学会用事物在全过
程中的发展变化规律来确定它在某一时刻的状态。
