圆周角

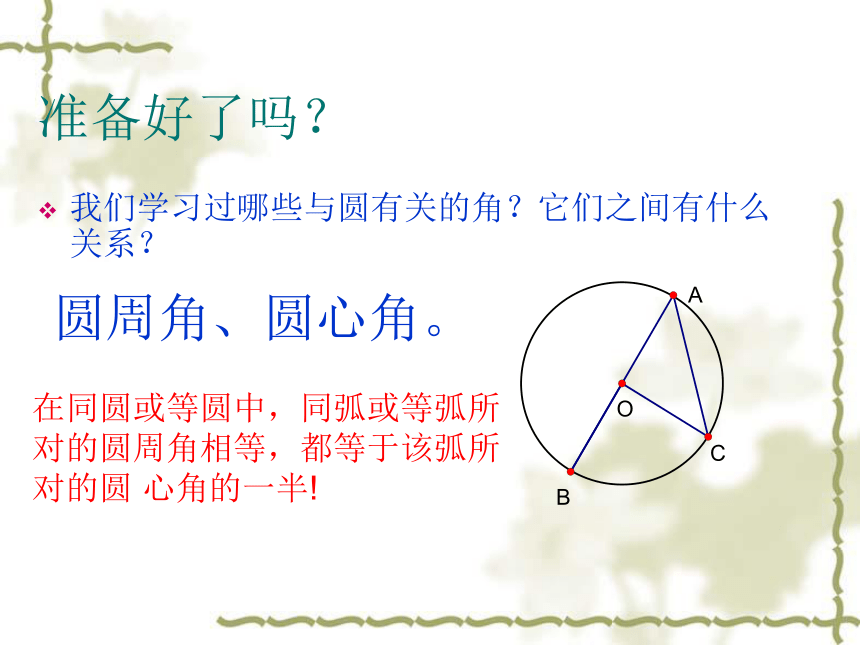
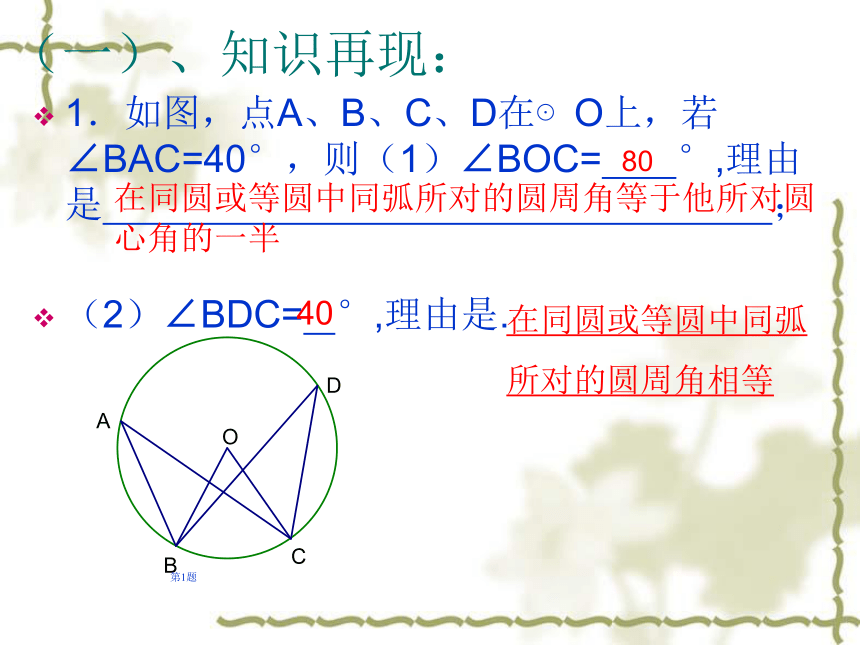
课件12张PPT。 圆周角2欢迎来到数学课堂准备好了吗？我们学习过哪些与圆有关的角？它们之间有什么关系？圆周角、圆心角。在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆 心角的一半!（一）、知识再现：1．如图，点A、B、C、D在⊙O上，若∠BAC=40°，则（1）∠BOC= °,理由是 ；
（2）∠BDC= °,理由是. 第1题80在同圆或等圆中同弧所对的圆周角等于他所对圆心角的一半40在同圆或等圆中同弧
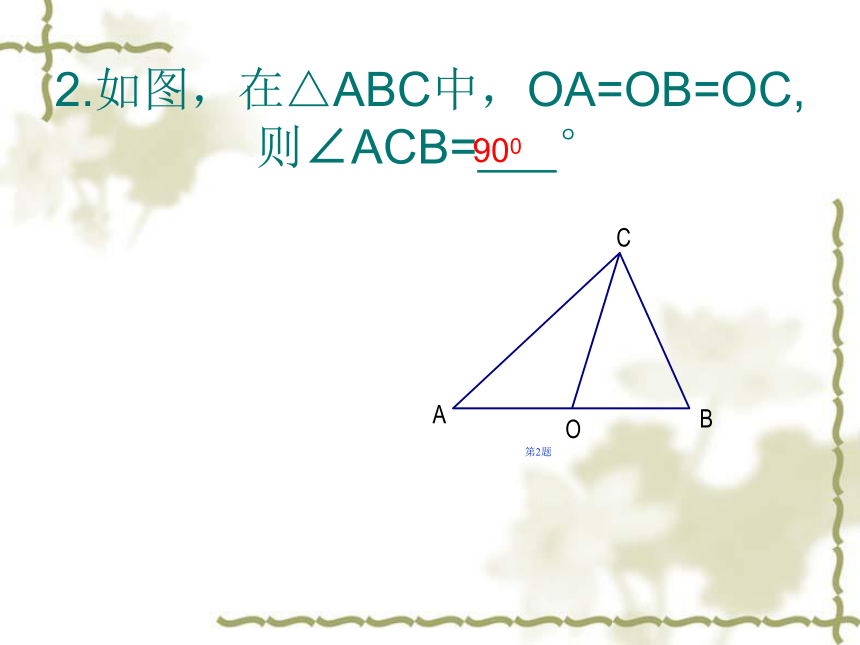
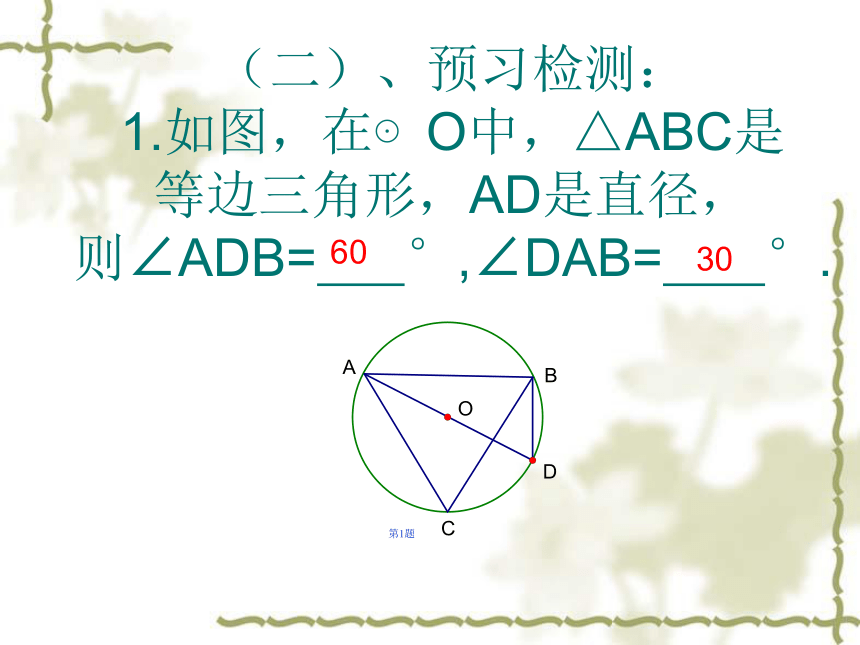
所对的圆周角相等2.如图，在△ABC中，OA=OB=OC,则∠ACB= ° 第2题900（二）、预习检测：1.如图，在⊙O中，△ABC是等边三角形，AD是直径，则∠ADB= °,∠DAB= °. 第1题60302. 如图，AB是⊙O的直径，若AB=AC，求证：BD=CD 第2题证明：连结AD∵ AB是⊙O的直径
∴∠ADB=900(直径或半圆所对的圆周角是直角。)又∵AB=AC
∴BD=CD(等腰三角形三线合一)探索活动一如图，BC为⊙O的直径，它所对的圆周角是锐角、钝角，还是直角？为什么？半圆所对的圆心角∠BOC=1800所以∠BAC=900（在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于该弧所对的圆 心角的一半）如图，圆周角∠A=90°，弦BC经过圆心吗？为什么？连结OB、OC探索活动二归纳自己的结论：1、直径或半圆所对的圆周角是直角,
2、900的圆周角所对的弦是直径。由圆周角∠A=90°，得∠BOC＝1800
，即BOC在一条直线上。例题1.如图，AB是⊙O的直径，弦CD与AB相交于点E，∠ACD=60°，∠ADC=50°,求∠CEB的度数.感受新知：小提示：利用直径所对的圆周角是直角的性质 解：连结BD∵AB是⊙O的直径
∴∠ADB=900(直径所对的圆周角是直角)
∵∠ADC＝500
∴∠EDB=∠ADB-∠ADC=900-500=400
∴∠ ABD=∠ACD=600(同弧所对的圆周角相等)
∴ ∠CEB=∠B+∠EDB=600+400=1000例题2.如图，△ABC的顶点都在⊙O上，AD是△ABC的高，AE是⊙O的直径.△ABE与△ACD相似吗？为什么？解：△ABE与△ ACD相似利用直径所对的圆周角是直角的性质解题.2、如图，△ABF与△ACB相似吗？ 如图， A、B、E、C四点都在⊙O上，AD是△ABC的高，∠CAD=∠EAB,AE是⊙O的直径吗？为什么？ 利用 90°的圆周角所对的弦是直径. 自我挑战：四、知识梳理1.两条性质： 2. 直径所对的圆周角是直角是圆中常见辅助线.作业：1.如图，AB是⊙O的直径，∠A=10°,则∠ABC=_.
2.如图，AB是⊙O的直径，CD是弦，∠ACD=40
则∠BCD=_______,∠BOD=_______.
3.如图，AB是⊙O的直径，D是⊙O上的任意一点(不与点A、B重合)，延长BD到点C，使DC=BD，判断△ABC的形状：__________。
4.如图，AB是⊙O的直径，AC是弦，∠BAC=30°,则AC的度数是( )
A. 30° B. 60° C. 90° D. 120°