二次函数图像及性质(2)

课件12张PPT。第六章
二次函数的图象和性质(2)
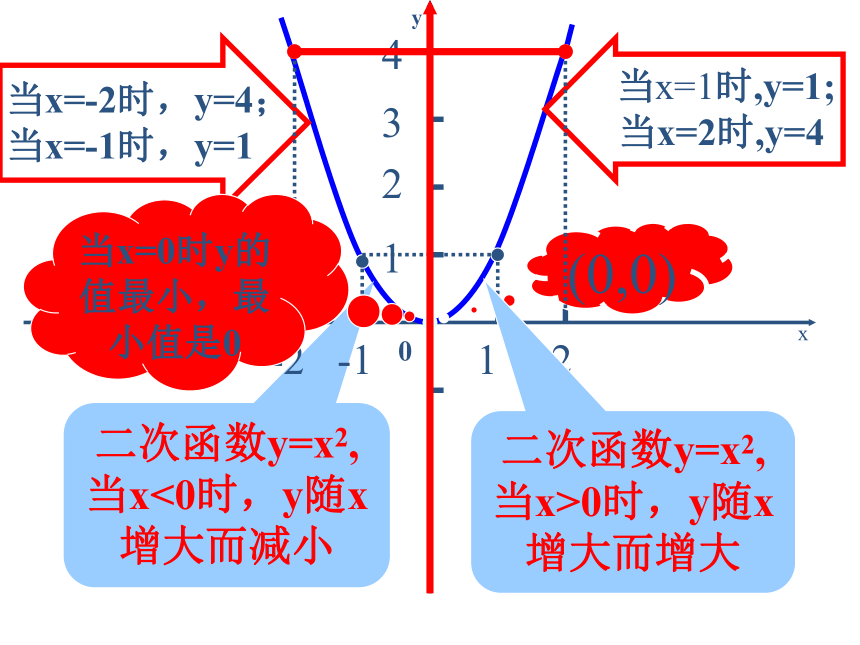
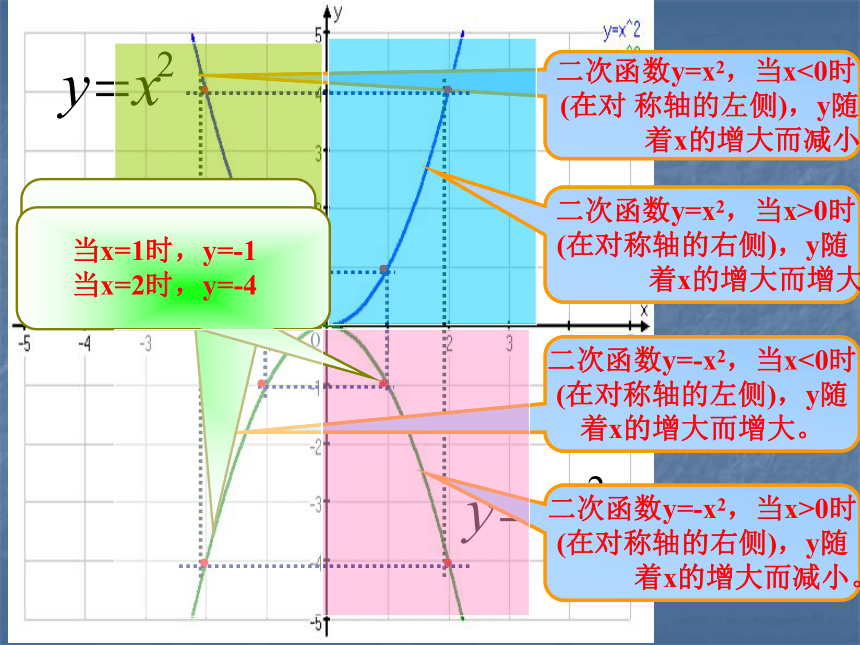
当x=-2时，y=4；
当x=-1时，y=1 当x=1时,y=1;
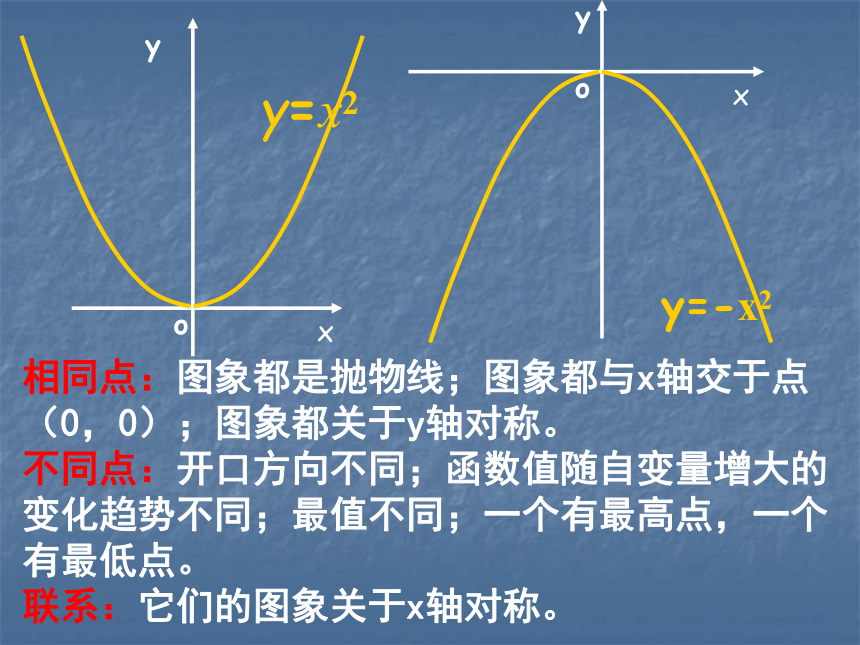
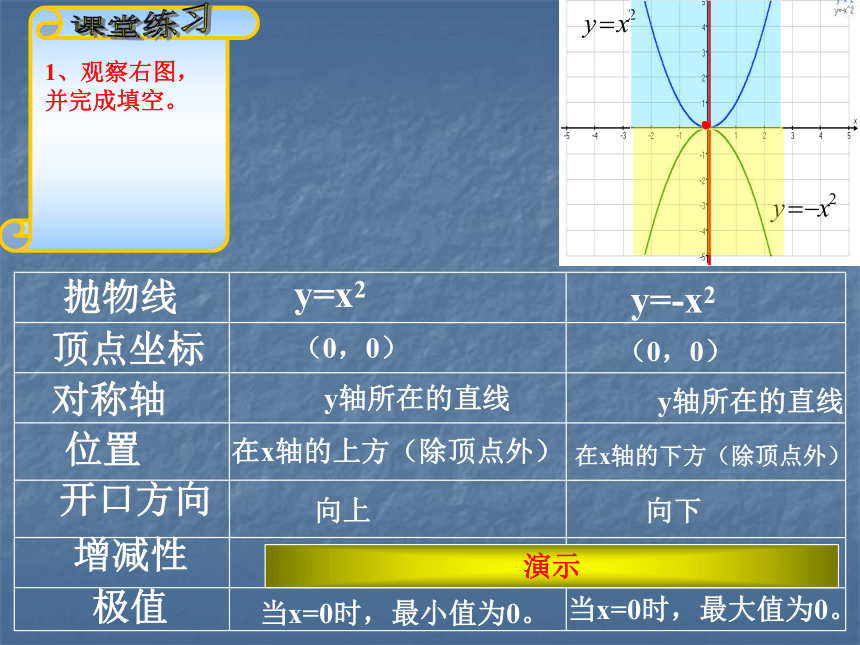
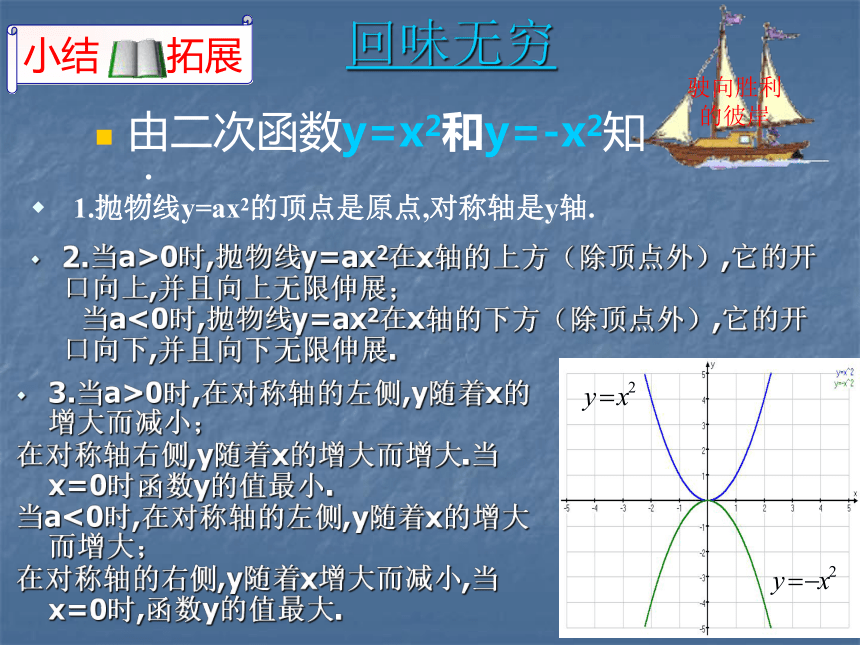
当x=2时,y=4二次函数y=x2,当x<0时，y随x增大而减小-1-2 1 2 1 2 3 4(0,0)当x=0时y的值最小，最小值是0二次函数y=x2,当x>0时，y随x增大而增大0xyyxxy=x2y=-x2yoo相同点：图象都是抛物线；图象都与x轴交于点（0，0）；图象都关于y轴对称。 不同点：开口方向不同；函数值随自变量增大的变化趋势不同；最值不同；一个有最高点，一个有最低点。 联系：它们的图象关于x轴对称。（0，0）（0，0）y轴所在的直线y轴所在的直线在x轴的上方（除顶点外）在x轴的下方（除顶点外）向上向下当x=0时，最小值为0。当x=0时，最大值为0。演示回味无穷2.当a>0时,抛物线y=ax2在x轴的上方（除顶点外）,它的开口向上,并且向上无限伸展；
当a<0时,抛物线y=ax2在x轴的下方（除顶点外）,它的开口向下,并且向下无限伸展.3.当a>0时,在对称轴的左侧,y随着x的增大而减小；
在对称轴右侧,y随着x的增大而增大.当x=0时函数y的值最小.
当a<0时,在对称轴的左侧,y随着x的增大而增大；
在对称轴的右侧,y随着x增大而减小,当x=0时,函数y的值最大.1.抛物线y=ax2的顶点是原点,对称轴是y轴.由二次函数y=x2和y=-x2知： 二次函数y=x2，当x<0时
(在对 称轴的左侧)，y随
着x的增大而减小。 二次函数y=x2，当x>0时
(在对称轴的右侧)，y随
着x的增大而增大。
二次函数y=-x2，当x<0时
(在对称轴的左侧)，y随
着x的增大而增大。
二次函数y=-x2，当x>0时
(在对称轴的右侧)，y随
着x的增大而减小。 0我思，我进步1.已知抛物线y=ax2经过点A（-2，-8）.
（1）求此抛物线的函数解析式；
（2）判断点B（-1，- 4）是否在此抛物线上.
（3）求出此抛物线上纵坐标为-6的点的坐标.知道就做别客气2.填空:(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧,
y随着x的增大而增大；在
侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外).（0，0）对称轴
的右对称轴的左00上(2)抛物线 在x轴的 方(除顶点外),在对称轴的左侧,y随着x的 ；在对称轴的右侧,y随着x的 ,当x=0时,函数y的值最大,最大值是 ,
当x 0时,y<0.下增大而增大增大而减小0活动与探索已知二次函数y=mxm2+m当m取何值时它的图象开口向上。 （1）当x取何值时y随x的增大而增大。
（2）当x取何值时y随x的增大而减小。
你认为今天这节课最需要掌握的是 ________________ ？ 你知道吗